不同尺寸褶皱对风电叶片主梁性能的影响研究

文 | 赵春妮，刘清，陈文光，李军向

风电叶片的主梁主要由单向纤维成型，单向复合材料结构的典型设计极限是压缩强度极限。众所周知，纤维的直线度对复合材料的压缩强度有很大的影响。纤维在铺层或固化过程中产生的褶皱会使局部应力状态恶化，导致局部基体屈服、纤维微屈曲和扭结或在纤维/基体界面发生断裂。因此，褶皱的存在会大幅降低叶片的强度，最终导致叶片提前失效。叶片作为风电机组的重要部件，成本占整机制造成本的22%左右，再加上发电量的损失、叶片的运输和吊装成本，叶片失效造成的损失无疑是巨大的。

当前，行业已经意识到了褶皱的危害，也开展了很多关于褶皱的研究，包括定性和定量分析。定性分析主要是从褶皱产生机理出发，从材料、工艺、模具、检验、人员、标准以及修复等方面对产生褶皱缺陷的主要原因进行研究分析；定量分析包括有限元仿真分析和试验对比分析：有限元分析通过建立含褶皱的有限元模型，分析受压状态下，褶皱不同层数、宽度、高宽比等因素对风电叶片强度的不同影响；试验分析通过制作不同类型的褶皱试件，对比不同高宽比、不同偏移角度的褶皱对叶片主梁材料疲劳性能的影响。其中，西门子公司与美国西北大学对其合作制作的褶皱试件进行了静力、疲劳测试，并详细记录了褶皱的发展过程，该研究增进了行业对褶皱的认识。

然而，当前针对褶皱的已有研究并不全面，不能涵盖实际运维中经常遇到的问题。本文试图从仿真的角度对如下问题进行解答：（1）当前主要以褶皱的高宽比来描述褶皱尺寸和比较褶皱性能，相同高宽比、不同尺寸的褶皱性能差别有多大？（2）当褶皱缺陷占主梁宽度的比例较小时，如何判断褶皱缺陷对主梁性能的影响？（3）早期由于对褶皱的危害认识不足，相当数量存在褶皱缺陷的叶片被发往风电场，在褶皱损伤出现的早期，是否可以通过合适的方式予以排查？

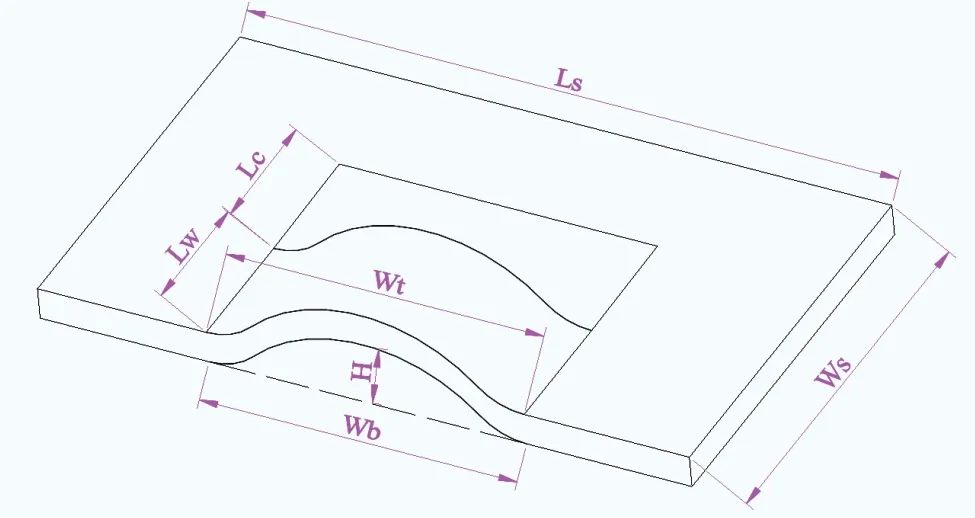
图1 褶皱尺寸

叶片褶皱的模型建立与仿真计算

本文以某长40m、主梁宽度420mm 的叶片为例进行研究。褶皱各尺寸参数分别为：高度2mm、底部宽度35mm、顶部宽度42mm、褶皱长度420mm。

一、褶皱模型建立

在叶片的设计和校核过程中，使用的是复合材料层合板的“表观”性能，即将复合材料单层视为均质材料，而没有考虑它由两种或多种组分材料构成这一事实。然而，根据对褶皱损伤的观察和国外的测试结果，褶皱的初始损伤出现在树脂上。为了得到更加精确的结果，本次模型按照细观力学的思想，将树脂和玻纤按照体积比分层建立。为了更加方便地描述褶皱的各个尺寸，如图1 所示定义各尺寸：Ls 表示主梁的长度，Ws 表示主梁的宽度，Lc 表示过渡区域的长度，Lw 表示褶皱的长度，Wt 表示褶皱顶部的宽度，Wb 表示褶皱底部的宽度，H 表示褶皱的高度。

为了简化褶皱模型，首先建立无褶皱的叶片整体模型，然后对叶片整体有限元模型加载设计疲劳载荷。在设计疲劳载荷My 的作用下，得到L20m 附近PS 面主梁上轴向最大应力为73.6MPa，根据此应力计算得到褶皱模型的等效拉力为1238520.2N。

褶皱模型宽度和铺层按照上述叶片距叶根20m 位置实际宽度和铺层设定，褶皱尺寸按照测得尺寸设定，建立长度为1m 的平板有限元模型。取树脂与玻纤的体积比为53:47，褶皱弧线参照实际模型采用同心圆建立，并与平面区域进行倒角处理，所建模型如图2 所示，绿色区域代表树脂，紫色区域代表玻纤。将模型一端固支，根据叶片整体有限元模型计算得到的应力，在另一端施加等效拉力。

二、褶皱模型分析

根据GL 规范，叶片容许载荷循环次数N 应按下式确定：

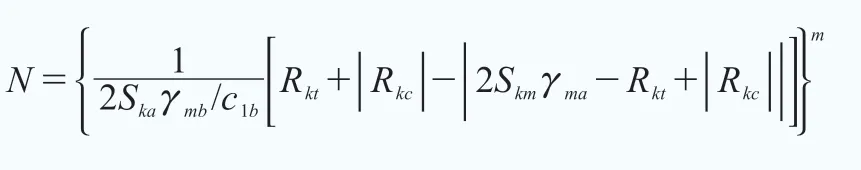
式中，Skm为特征载荷平均值；Ska为特征载荷幅值；Rkt为结构元件拉伸强度特征值；Rkc为结构元件压缩强度特征值；m为S-N曲线斜率，m＝10。

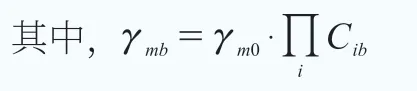
图2 褶皱模型

图3 褶皱位置树脂应力

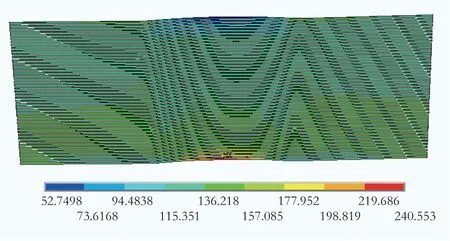
图4 褶皱位置玻纤应力

树脂是各向同性的材料，需要综合考虑各个方向的应力。如图3 所示，分析得到褶皱区域树脂材料mises 等效应力分布。在疲劳载荷作用下，树脂最大等效应力出现在褶皱边缘区域，为22.6MPa。对于树脂可使用年限的计算方法，国内外尚无较为成熟的理论，暂选用Goodman 公式进行计算。树脂材料拉伸强度取67MPa，S-N 疲劳曲线取斜率m=8。考虑到老化、温度、后固化影响，取折减系数为1.634，计算得到树脂寿命小于1 年（0.06 年）；若不考虑上述因素的影响，取折减系数为1 时，计算可得树脂寿命为3.05 年。

图5 试验过程

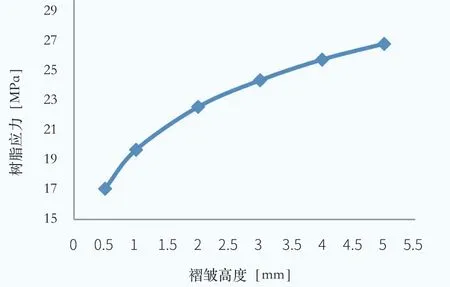
图6 相同高宽比、不同褶皱高度的树脂应力

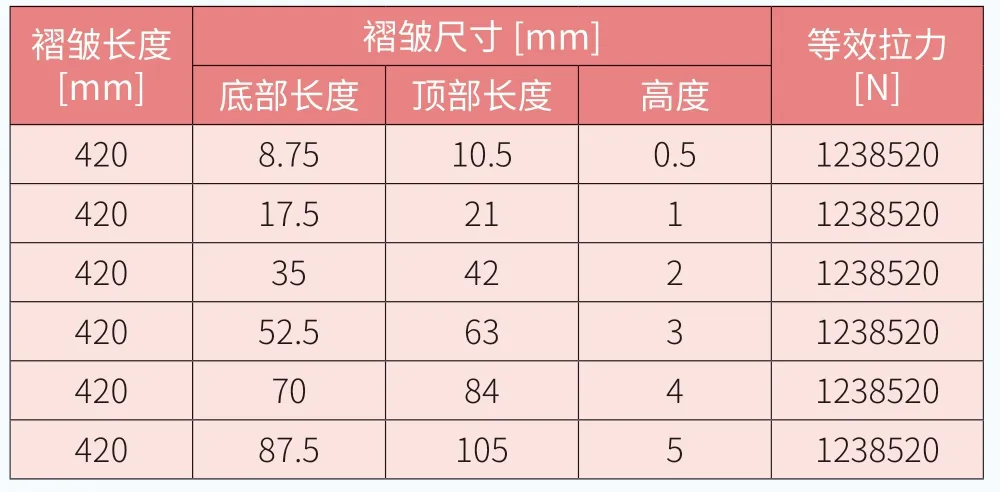
表1 相同高宽比、不同褶皱高度的树脂应力

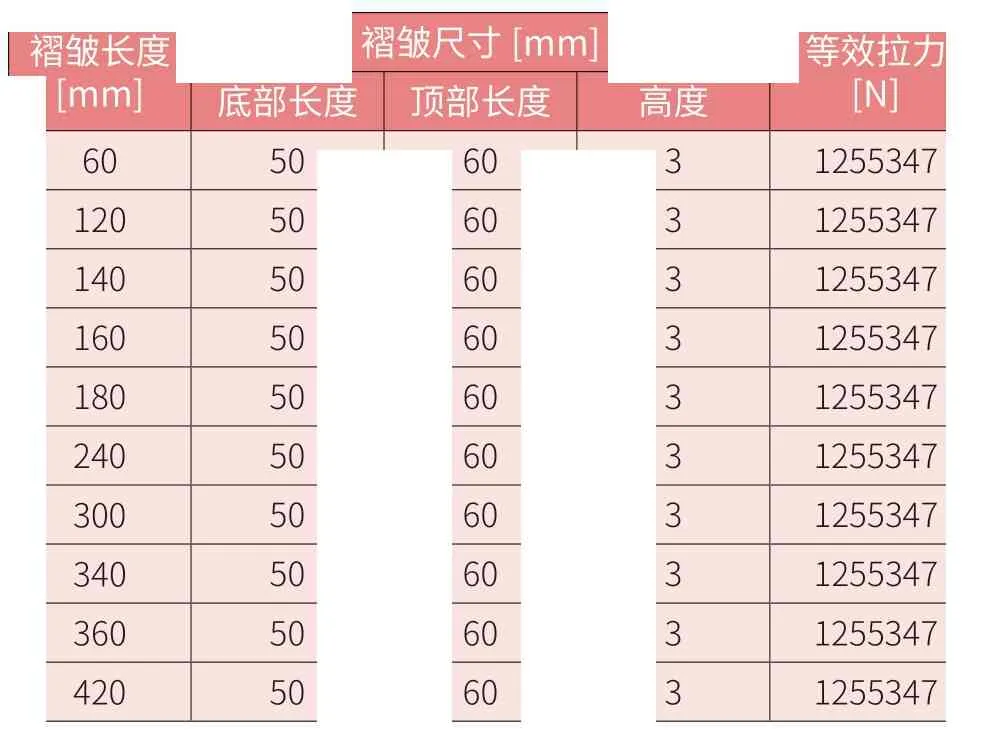
表2 相同高宽比、不同褶皱长度的树脂应力

玻纤在纤维主方向的应力为240.5MPa，同样按上述方法，考虑折减系数为1.485 时，玻纤寿命为6.5 年；若折减系数为1，玻纤寿命为339 年。

三、褶皱模型分析结果与国外试验结果对比

西门子公司与美国西北大学合作对多种尺寸的褶皱试件（长宽高尺寸为275mm×13mm×30mm，褶皱宽度为7～11 mm，高度为2～3mm）进行了测试，并详细记录褶皱从初始损伤到失效的全部过程，疲劳试验取应力比 R=－1，测得同样大小、无褶皱的式样可循环次数为2E6，发现多数式样可循环次数在1E3 与8E5 之间，在目标循环次数完成之前就发生了失效。疲劳试验中得到的失效区域与图3 一致，发生在褶皱的边缘位置。典型的损伤扩展过程如图 5 所示：（a）初始式样无损伤；（b）褶皱区域厚度出现单一的分层；（c）分层数在式样厚度方向增加；（d）式样最终发生失效。

该试验结果与本文仿真结果一致，二者均表明在叶片运行中褶皱缺陷的初始损伤发生在树脂上，具体表现为主梁的分层。复合材料的分层会导致透光不均匀，这个特征有助于褶皱损伤早期的检测和识别。

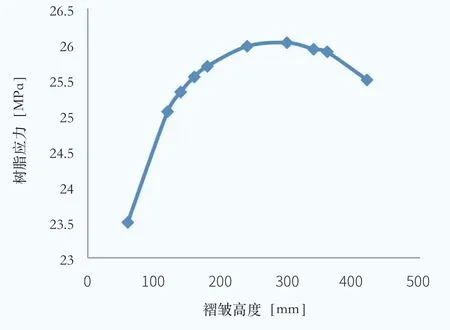
图7 相同高宽比、不同褶皱长度的树脂应力

不同尺寸褶皱对主梁性能的影响

由于褶皱处树脂早于玻纤失效，以下通过比较不同情况下树脂的应力获得褶皱初始损伤的情况。

一、高宽比相同、褶皱高度不同时的应力比较

仍以上述叶片为例，在高宽比相同的情况下，对比不同褶皱高度树脂的应力情况，各种褶皱尺寸详见表1，模型建立和计算过程同上文所述，得到应力结果如图6 所示。

由计算结果可知：高宽比相同时，随着褶皱高度的增加，树脂的应力增大—在褶皱高度较小时，随着褶皱高度增加，应力变化幅度较大；当高度增大到一定值时，随着褶皱高度增加，应力变化幅度呈减小的趋势。

二、高宽比相同、褶皱长度不同时的应力比较

部分叶片的褶皱仅占整个主梁宽度的一部分，为分析此类叶片，按照上文方法重新建立褶皱局部模型，有褶皱的区域与无褶皱区域通过斜线过渡，为使过渡较为平滑，过渡区域长度取值为30mm，主梁宽度仍为420mm，剩余部分为无褶皱区域。褶皱不同长度详见表2，计算过程同上文所述，得到应力结果如图7 所示。

由计算结果可知：在褶皱截面尺寸不变的情况下，随着褶皱长度的增加，褶皱处树脂应力呈抛物线变化趋势—当褶皱长度小于主梁宽度的约2/3 时，随着褶皱长度增加，树脂应力逐渐增大，当褶皱长度介于主梁宽度的1/3 与2/3之间时，树脂应力变化幅度在0.5MPa 范围内；当褶皱长度大于主梁宽度的约2/3 时，随着褶皱长度增加，树脂应力反而逐渐减小。

结论

本文分析结果，可为褶皱叶片的排查和检测提供以下参考：

（1）褶皱缺陷最初始的损伤出现在树脂上，最先表现为褶皱边缘处的分层。因此，明确损伤类型，及时发现褶皱早期损伤并进行针对性维修或更换，可以最大程度减低风电场褶皱叶片的运维成本。

（2）相同高宽比的褶皱，随着高度增加，应力也在增大，只依靠高宽比并不能准确描述褶皱的性能。

（3）在相同高宽比的情况下，长度为主梁宽度的三分之一与等同于整个主梁宽度的褶皱应力接近，因此，不能忽略长度较短褶皱的危害。