一类二次算子族的数值域的MATLAB 图形实现

邢利刚，张新艳

（内蒙古财经大学统计与数学学院，呼和浩特 010071）

0 引言

利用算子的数值域估计算子的谱是谱估计的一种行之有效的方法，它的概念最早是由O. Toeplitz 在1918 年提出来的。线性算子A的数值域定义为：

这里A算子。D(A) 表示A的定义域，表示相应空间的内积。1919 年F.Hausdorff 证明了线性算子的数值域是凸集，随后对线性算子的数值域的研究成果不断出现，并且不断的被推广，先后证明了矩阵的特征值包含在矩阵的数值域中；有界线性算子的点谱包含于其数值域中，其谱集是数值域闭包的一个子集等一系列成果Kato 在其专著[2]Perturbation Theory for linear operators 中将线性算子的谱包含关系推广到了闭线性算子的情形,得到了无界线性算子谱包含于其数值域的闭包的充分条件是：W(A)的每一个连通分支中都至少含有A 的一个正则点。同时得到了算子A 的预解集估计，对有 (A-λ)-1≤dist(λ,W(A))。文献[3-6]主要讨论了算子的数值域和二次算子族的相关概念和性质。在文献[1]中我们给出了这类二次算子族的数值域的刻画和估计表达式，本文我们利用MATLAB 软件绘制了M,K,A取不同类型的复数矩阵时的二次算子族L(λ)=Mλ2-iKλ-A的数值域的图形，从图形的结果看，更好的证明了我们文献[1]的结果的正确性。

1 基础知识

结论1二次算子族

L(λ)=Mλ2-iKλ-A：D(L(λ))=D(M)∩D(A)∩D(K)

满足：

Ker(M)∩Ker(K)∩Ker(A)={0}

且M，K，A是自伴算子，则：

结论2二次算子族

L(λ)=Mλ2-iKλ-A，D(L(λ))=D(M)∩D(A)∩D(K)

轰炸停止了，飞机的轰鸣声渐渐远去。夏国忠用手刨开面前堆积起来的泥土，爬出掩体，朝山下望去。他看见，鬼子分成几路正开始向山头进攻。他回头向身边的副连长下达命令：“把战士们都叫出来，准备反击。”

满足：

Ker(M)∩Ker(K)∩Ker(A)={0}

且M,K,A是自伴算子，则二次算子族的数值域关于虚轴对称。

结论3二次算子族

L(λ)=Mλ2-iKλ-A：D(L(λ))=D(M)∩D(A)∩D(K)

满足：

Ker(M)∩Ker(K)∩Ker(A)={0}

且M，K，A是自伴算子，则：

W0(L)=W1∪W2

其中：

2 主要算例

算例1：

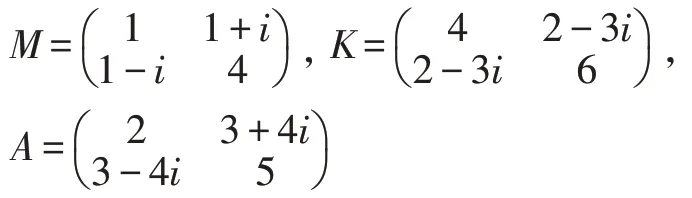
MATLAB 绘图结果如图1。

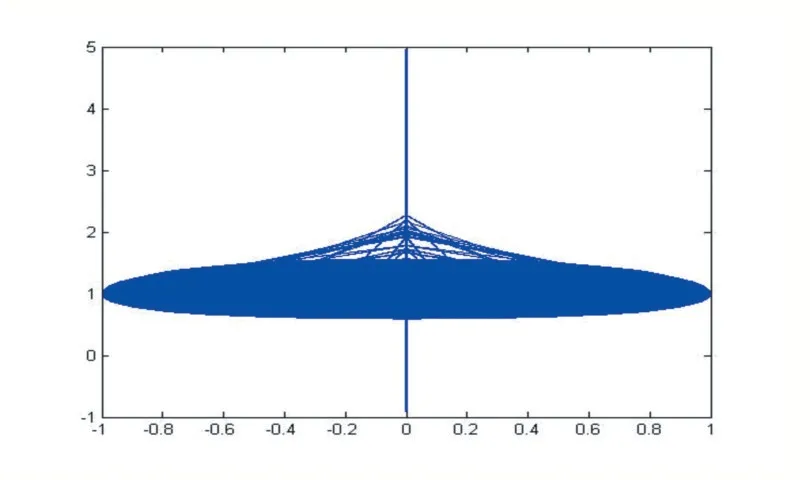
图1

算例2：

MATLAB 绘图结果如图2。

图2

算例3:

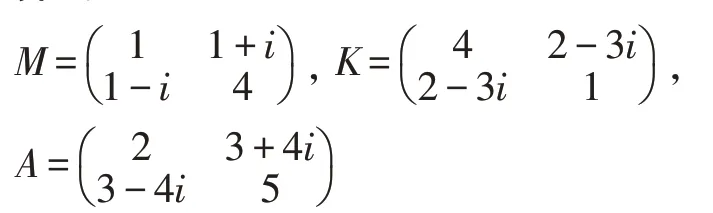
MATLAB 绘图结果如图3。

图3

在做算例的过程中，我们主要想得到这类二次算子族中，M,K,A三个算子对该类二次算子数值域的影响程度，如果我们找到了它们之间的内在的联系，应该是一件非常有意思的事情。