错误方法为何总得到正确结果？——对一道数列题的错解的反思

雷亚庆

(江苏省南京市大厂高级中学 210044)

一、错解演示

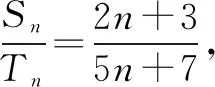
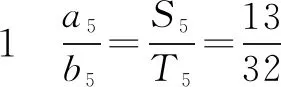
师：为什么这样想？

生：跟着感觉走，感觉a5应该和S5有关.

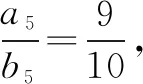
反思：学生对老师的解法提出自己的疑问甚至质疑实际上是非常非常难得的.这个时候如果我们老师为了赶进度或者是感觉学生对自己不礼貌而匆忙应付过去甚至恼火，那就会大大挫伤学生的学习积极性，最可怕的是学生会因此而失去质疑能力.没有质疑，何来创造力，于是教师停下来和学生对这个问题进行了深入的探讨.

教师分析：

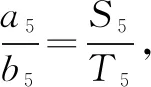
化简得a1d1=b1d2.

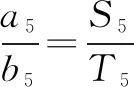
错解2 由题意可设Sn=k(2n+3),Tn=k(5n+7),

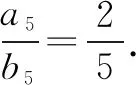
师：为什么这么做？

生：利用Sn与an的关系.

师：知道错因了吗？

生：Sn与an的关系不会错，应该是Sn的表示有问题.

师：大家讨论一下出现什么问题.

生：等差数列的前n项和应该是关于n的一个二次函数形式，而错解2中的是一次函数形式.

二、正解演示与提升

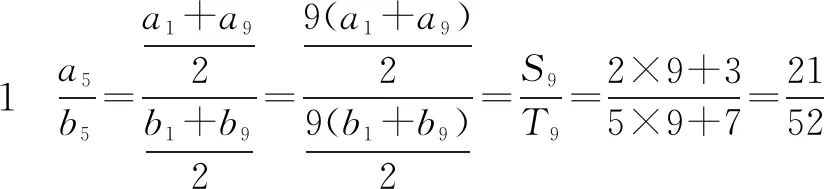
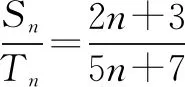
所以可设：Sn=kn(2n+3),Tn=kn(5n+7).

所以a5=S5-S4=65k-44k=21k，b5=T5-T4=160k-108k=52k.

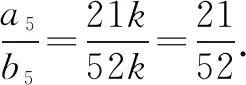
巡回中教师发现学生大都采用方法1，然后追问学生为什么喜欢用方法1？学生的回答很直接，简单运算少.于是教师抛出下面一个问题.

三、预设中的变式探究

学生给出以下两种解法

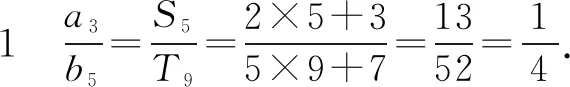
解法2Sn=kn(2n+3),Tn=kn(5n+7),

则有a3=S3-S2=27k-14k=13k，b5=T5-T4=160k-108k=52k.

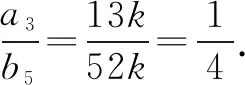
师：大家评价一下以上两种解法.

师：那应该是什么呢？

因为还有其他错题要订正，笔者就准备就此打住，于是笔者总结：“同学们，通过刚才这个变式我们应该认识到解法2才是解决这类问题的通法，虽然解法1在解决下标相同的两项之比时有些优势，但解决下标不同时就会出现错误.刚才这个同学说得很好，解法1显然是有问题的，解法1的结果对应该是偶然的！大家只要记住用解法2做就可以万无一失了.”

四、意外生成与收获

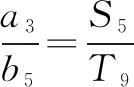
学生的话引起了教师的深思，是含糊带过还是回去认真研究一番呢？笔者决定索性和学生当堂好好探究一番.学生会质疑，说明学生经过认真思考，这是多么值得保护的品质啊！

经过师生共同探究，终于找到了原因：

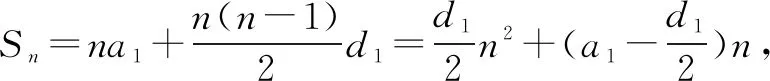
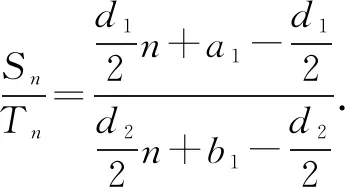
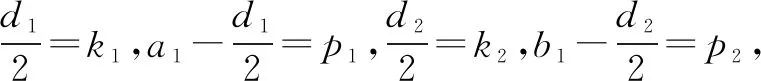
f(n)=k1n+p1,g(n)=k2n+p2.

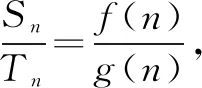
另一方面：

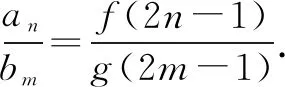
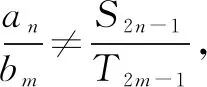
于是就出现了上面神奇的一幕.

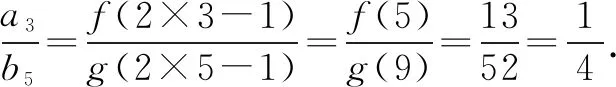
五、一点反思

很多同学在认可或听懂了老师的正确解法后，往往会认为自己的方法得到的答案与标准答案不一样,所以是错的，至于为何错，错在哪里？解法有没有意义？学生往往会忽略.这时候如果停下来，多问问学生为什么错？你当时的想法是什么？也许就可以帮助学生真正理解数学概念，做到知其然也知其所以然.