递归数列在计数中的应用

周天明

(安徽省合肥市第六中学 230001)

人教A版数学教材,必修5第二章的阅读与思考,是关于我国古老智力游戏九连环的相关内容,书中利用数列的有关知识,解决了解开九连环最少需要移动圆环次数问题,在选修2-2中,又以例题的形式提出了汉诺塔问题,同样也利用数列的有关知识,解决了铁片最少需要移动次数问题.在排列组合问题中也存在类似的解决问题的方法.这两个问题都是计数问题,都使用了所谓的递归数列法,按照某种标准找出递推关系式，并求出取第一个值(或前几个值)时的各项，然后代入递推关系式，得出所要求的结果.将计数问题化归为数列问题,通过递推关系式求出数列的通项公式或数列中的某一项.这类问题需要对题设中所给出的递推关系式进行分析、推理、变形等处理，发现规律才能达到所要解决问题的目的.实际上很多计数问题都可以用递归数列法,以下介绍其在几种典型问题中的应用.

问题1 (上楼梯问题)有一楼梯共n级,如果规定每次只能跨上一级或两级,问要登上第n级楼梯,共有多少种不同的走法？

解析设登上第n级楼梯有an种走法，而登上第n级走法可以分为两类,第一类是第n-1级跨一级，第二类是从第n-2级跨两级，根据加法原理有an=an-1+an-2，又a1=1,a2=2.

设递推数列可化成an-λan-1=μ(an-1-λan-2)，即an=(μ+λ)an-1-λμan-2，比较对应的系数，

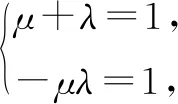
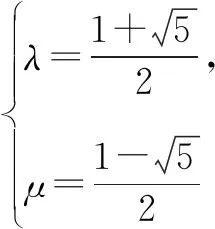
①

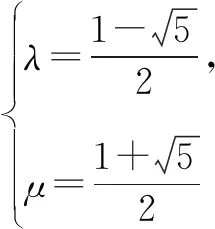
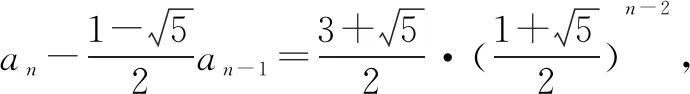
②

问题2 (圆形染色问题)如图所示，将圆n等分得到n块区域M1,M2,M3,…,Mn(n≥2)，现取k(k≥2)种颜色对这n块区域染色，要求每相邻的两个区域染不同色，共有多少种不同染色方案？

解析设k种颜色对n块区域染色，要求每相邻的两个区域染不同色，共有an种不同染色方案．区域M1有k种染色方案，区域M2有k-1种染色方案，区域M3也有k-1种染色方案，…，区域Mn也有k-1种染色方案，共有k·(k-1)n-1种染色方案．显然上述计数中包含区域M1和区域Mn同色的情况，故要排除这种情况．若区域M1和区域Mn同色，则可以把区域M1和区域Mn看成是同一个区域，根据假设知此时，有an-1种染色方案，故an=k·(k-1)n-1-an-1，又a2=k(k-1),a3=k(k-1)(k-2)，设递推式可化为an-t(k-1)n=-[an-1-t(k-1)n-1],即an=-an-1+tk(k-1)n-1，与原递推式比较对应系数，得t=1.所以有an-(k-1)n=-[an-1-(k-1)n-1]，可见数列{an-(k-1)n}从第2项k-1起成公比为-1的等比数列，所以an-(k-1)n=(k-1)·(-1)n-2，故an=(k-1)n+(k-1)·(-1)n(n≥2).

问题3 (传球问题)有m个人做相互传球练习，第一次甲先传球给其余m-1人中一人,第二次由拿球者再传给其余m-1人中的一人,这样共传了n次球,则第n次传球仍传回到甲的传法种数共有多少种?

解析记第n次传球时球仍传回到甲的传法种数为an，易得a1=0,a2=m-1，要第n次传球时球正好又传回到甲,必需第n-1次传球时球正好不传到甲. 因为前n-1次传球共有(m-1)n-1种不同传法，其中第n-1次传球传回到甲的传法有an-1种，所以第n-1次传球没有传回到甲的传法有(m-1)n-1-an-1种，在这(m-1)n-1-an-1种情况中，只要第n次传球时球正好传回到甲即可,故得递推数列an=(m-1)n-1-an-1.

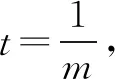
问题4 (全错位排列问题)有n个不同的元素,它们一一对应于n个位置，如果这n个元素都不排在自身对应的位置上,这种排列的方法称为n个元素的一个全错位排列.n个元素都不排在自身对应的位置上的全错位排列共有多少种？

解析设这n个不同的元素分别为b1,b2,…,bn，并设元素bi对应的位置为i(i=1,2,…,n)，并记n个元素都不排在自身对应的位置上的不同排列有an种.

n个不同元素的一个全错位排列可分成二个步骤:

第一步，先决定元素b1的排法,可以排在位置2,3,…,n，共有n-1种不同排法；

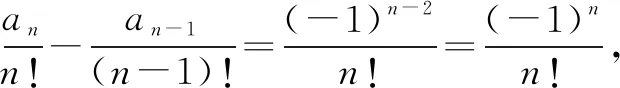
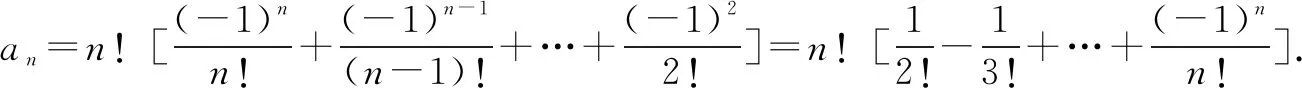
章建跃先生提出以课本为本才是好的数学教学.我们在平时的教学中，要以教材为本，要重视教材中的例题和阅读材料的教学，教材的每一个角落都可能成为拓展的落脚点和生成点，也是命题的切入点，基于教材进行适度拓展，不但可以提高学生的学习兴趣，也可以提高提高学生提出问题和解决问题的能力，一举两得，何乐而不为.