见微知类 以少胜多——不等式恒成立问题的常用解法

黄光鑫 武 婷

(四川师范大学附属中学 610000)

众所周知，不等式恒成立问题是高考数学中常考的一种重要题型，下面我们将选用一个题来全面介绍这一类题的常用解法，期望能对读者有所帮助.

例已知函数f(x)=lnx+ax2-(a+2)x(其中a>0).(1)讨论f(x)的单调性；

(2)若对任意的x∈(1,+∞)，关于x的不等式f(x)+2>0恒成立，求a的取值范围.

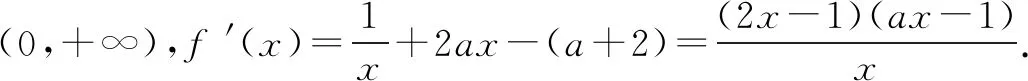
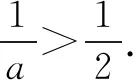
②若a=2，则f′(x)≥0,∴f(x)在(0,+∞)上单调递增.

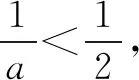
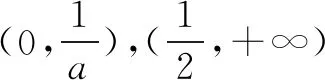
(2)解法一分类讨论(不分离参数).由(1)知：

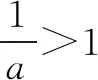
②若a≥2,f(x)在(1,+∞)上单调递增，则f(x)0.

综上所述，a的取值范围为[1,+∞).

解法二分离参数之全分离：有时需要用洛必塔法则处理端点情形.

解法三分离参数之半分离：先分离参数再通过切线进行放缩.

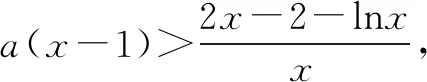
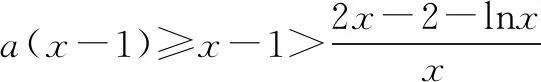
解法四发现零点，先必要后充分.记m(x)=f(x)+2=lnx+ax2-(a+2)x+2.∵m(1)=0,要使m(x)≥0在(1,+∞)上恒成立的一个必要条件是m′(1)≥0即a≥1.当x>1时x2-x>0，从而a(x2-x)≥x2-x.

∵m(x)=lnx+ax2-(a+2)x+2=lnx+2-2x+a(x2-x)≥lnx+2-2x+(x2-x)=lnx+2-3x+x2.

如果能证明在(1,+∞)上不等式lnx+2-3x+x2>0恒成立，则a的取值范围就是a≥1.

下面证明在(1,+∞)上不等式lnx+2-3x+x2>0恒成立.记r(x)=lnx+2-3x+x2.

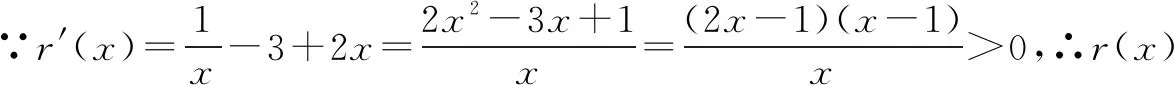
通过以上例题，我们可以看出解决不等式恒成立问题的常用方法有以下几种：(1)分类讨论[不分离参数]；(2)分离参数[半分离或全分离]；(3)先必要后充分.当然如果是选择题或填空题也可以采用数形结合的方法.希望大家能从这一个题中悟出这一类题的解法.数学学习就是要力求见微知类，以少胜多， 真正做到从尽可能少的题目中获得尽可能多的解题规律！

跟踪练习[2016高考新课标2文数]已知函数f(x)=(x+1)lnx-a(x-1).

(1)当a=4时，求曲线y=f(x)在(1,f(1))处的切线方程；

(2)若当x∈(1,+∞)时，f(x)>0，求a的取值范围.

答案：(1)2x+y-2=0；(2)(-∞,2].

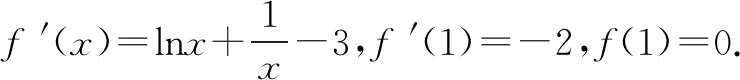
(2)解法一分类讨论[不分离参数].

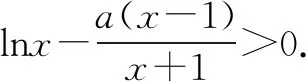
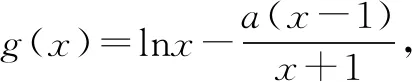
①当a≤2，x∈(1,+∞)时，x2+2(1-a)x+1≥x2-2x+1>0 ，故g′(x)>0,g(x)在x∈(1,+∞)上单调递增，因此g(x)>0.

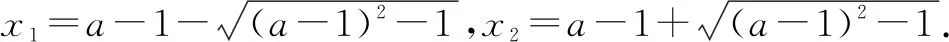
综上所述，a的取值范围是(-∞,2].

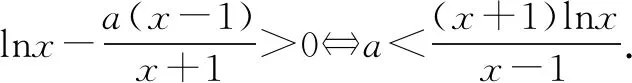
解法三先分离参数[半分离]，再通过切线进行放缩.

函数y=(x+1)lnx在点(1,0)处的切线方程是y=2(x-1).容易证明：当x>1时，(x+1)lnx≥2(x-1)，∴当a≤2,x>1时，a(x-1)≤2(x-1)，从而a(x-1)≤(x+1)lnx在x∈(1,+∞)上恒成立，所以a≤2.