对一道课本例题的解法探讨
彭光焰
(湖北省广水市第一高级中学 432700)
课本是几代人集体智慧的结晶,它具备相当完备的知识体系和能力架构系统,其中的例题和习题是学生解题能力的核心生长点,有些典型例习题由于其自身所蕴含的数学概念、数学思想、数学方法非常突出. 因此,在教学中利用好典型例习题,不仅可以在教学中强化基本概念、定义的教学,还要引导学生重视并运用定义解题,引导学生对课本的例题、习题进行多解、变式、迁移、整合、拓展. 因此,在教学中要切实把握好概念教学,这样既能提升学生运用数学概念分析问题和解决问题的能力,又能提升学生数学素养.
一、题目
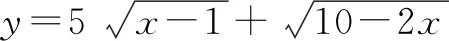
此题目是《普通高中课程标准实验教科书 数学 选修 4-5 人教A版 不等式选讲》第35页例2.
二、解法探讨
1. 利用柯西不等式求函数的最值
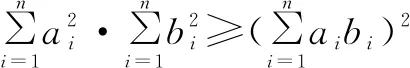
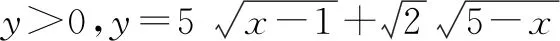
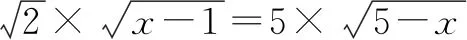
此解法是人教A版选修4-5提供的.
2. 利用判别式求函数的最值
思路分析2把函数转化为关于x的一元二次方程f(x)=0.由于方程有实根,故判别式Δ≥0,求得原函数的值域.
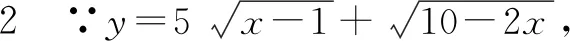
∴y>0,
∴y2-23x+15≥0.
由(y2-23x+15)2=100(x-1)(10-2x)得
729x2-(46y2+1890)x+(y4+30y2+1225)=0.
上述关于x的方程有实数根,
故Δ=(46y2+1890)2-4×729×(y4+30y2+1225)≥0,
即y4-108y2≤0,
0 3. 利用导数求函数的最值 思路分析3设y=f(x) 的导数为f′(x),可求得极值点.若函数定义域为[a,b],则最值必定在极值点或区间端点处取得. 4. 利用三角换元求函数的最值 思路分析4利用三角恒等式sin2α+cos2α=1将所给函数转化为值域容易确定的另一函数,进而求得函数最值. 以下同解法4. 令cos2θ=t,其中0≤t≤1. 5. 构造向量求函数的最值 思路分析5由向量不等式|a||b|≥|a·b|,可考虑用构造向量的方法进行求解. 由|a|2|b|2≥(a·b)2得 6. 利用方差求函数的最大值 思路分析6方差公式在数学解题中有着极其广阔的应用价值,充分利用方差s2非负性求函数最大值. ∵y=25a+2b, 7. 构造直线截距式求函数的最值 思路分析7求形如y=f(x)+g(x)函数最值,可以把f(x),g(x)当作是变量,即令v=f(x),u=g(x),φ(u,v)=0一般表示一条曲线,则y可以当作是y=v+u的直线在纵轴上的截距,因此截距的最小值也即是函数的最值. 8. 利用拉格朗日乘数法求函数最值 思路分析8用“拉格朗日乘数法”求函数f(u,v)在条件φ(u,v)=0条件下的最值,方法(步骤)是:1. 设拉格朗日函数l=f(u,v)+λφ(u,v),λ称拉格朗日乘数;2. 将l分别对u、v求偏导,得方程组,求出驻点P(u,v).如果这个实际问题的最大或最小值存在,一般说来驻点唯一,于是最值可求. 设拉格朗日函数为F(u,v)=f(u,v)+λg(u,v), 上面探讨可知,柯西不等式法,向量法,方差法只能求出函数的最大值,其它7种方法不仅可以求出最大值,而且可以求出最小值. 在平时的习题教学中,我们如果善于运用一题多解, 既发挥了例题的最大功效,拓宽了学生的学习视野,培养了学生的综合思维能力和创新能力,也提高了学生应试能力.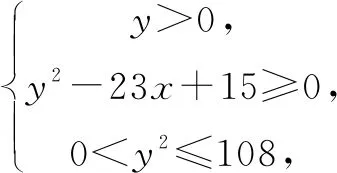
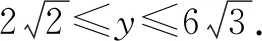
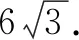
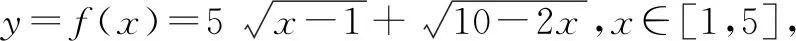
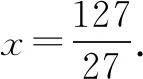
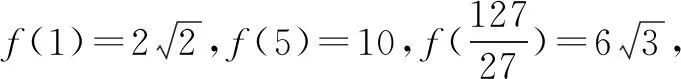



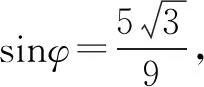
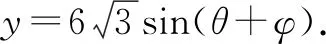
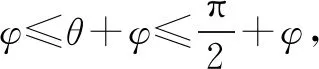
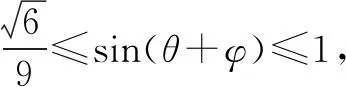
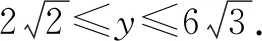
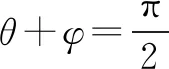
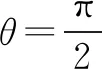
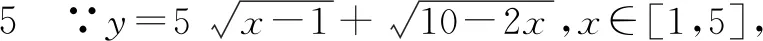
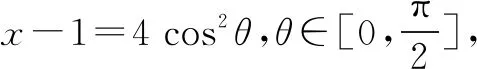
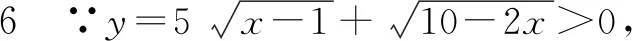
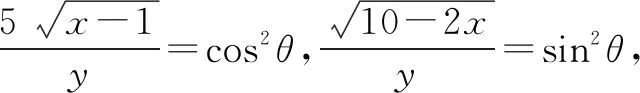
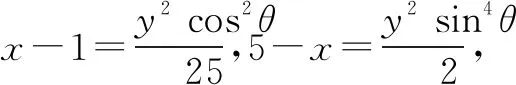
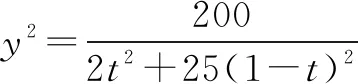
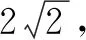
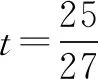
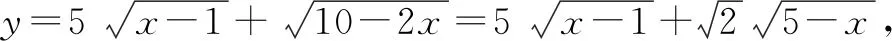
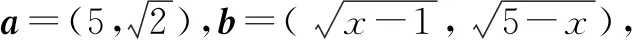
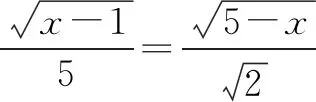
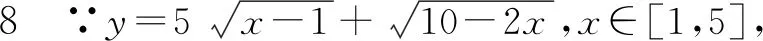
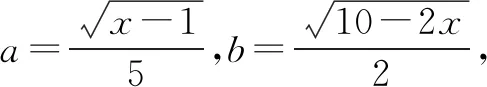
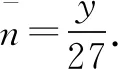
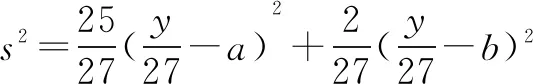
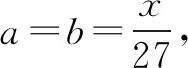
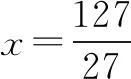
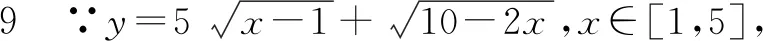
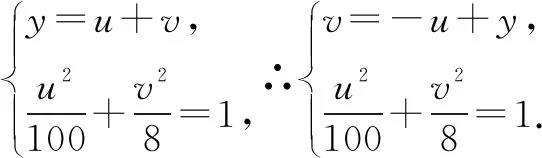
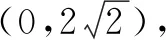
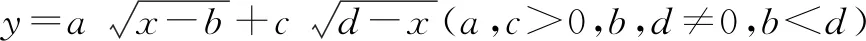
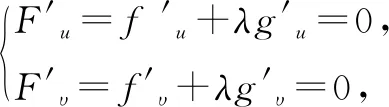
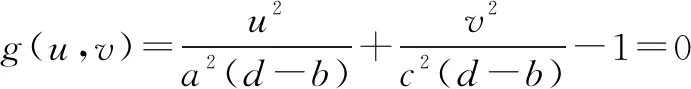
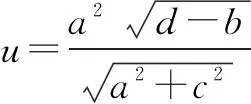
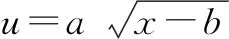
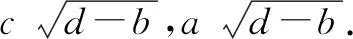
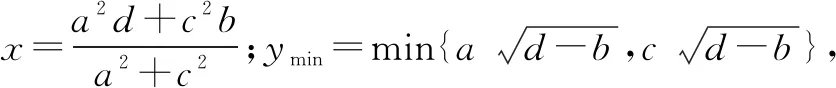
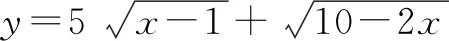
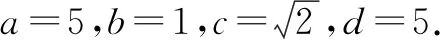
三、教学启示

