一道基本不等式试题的命制和思考

胡贵平

(甘肃省白银市第一中学 730900)

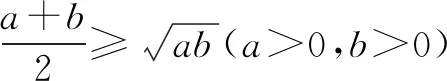
一、追根溯源

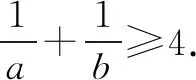
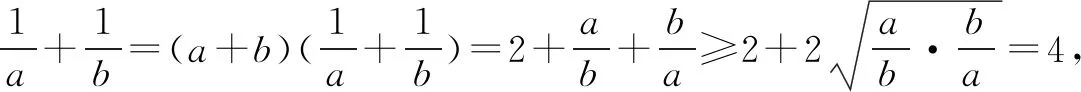
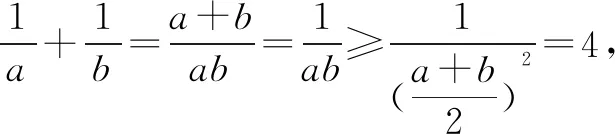
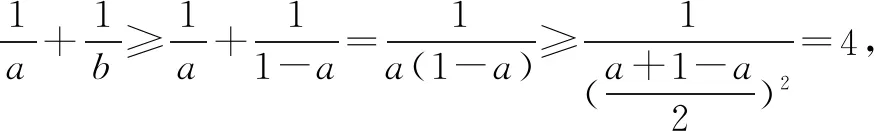
解法五 柯西不等式法由于a，b∈R+,a+b=1，

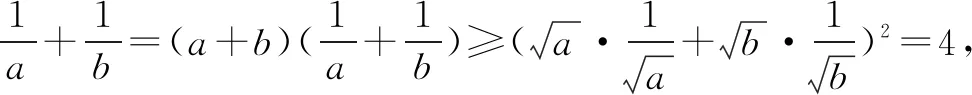
解法六 构造分布列法由于a，b∈R+,a+b=1，构造随机变量ξ的分布列

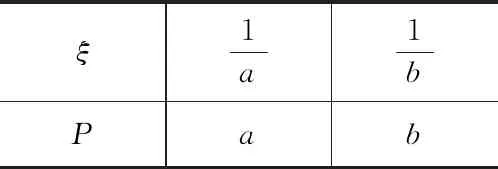
ξ1a1bPab

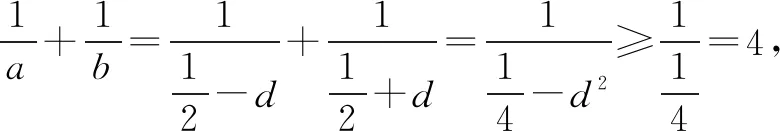
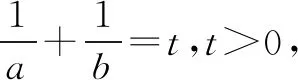
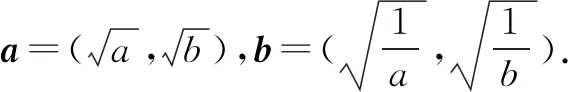
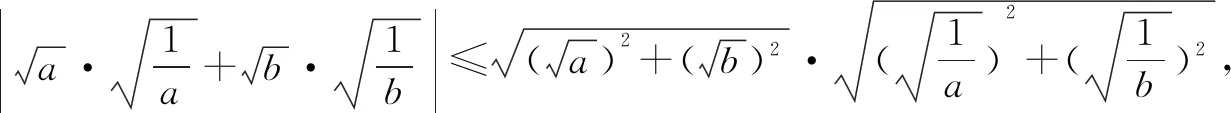
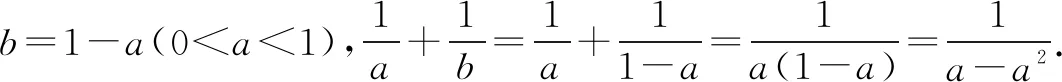
二、探究变式

这道课本习题考查了均值不等式求最值的运用，考查了变通能力.不等式既优美又简单，显然是不会直接拿出来作为高考题的．而高考呢？通常是采用“穿马甲”的方式对它进行改造和包装．

A． 8 B． 4 C． 1 D． 5

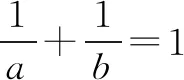
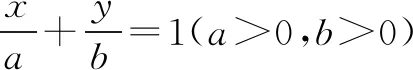
A．2 B．3 C．4 D．5

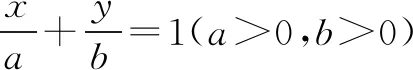
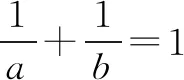
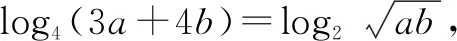
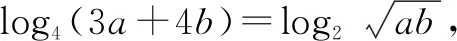
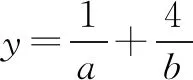
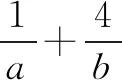
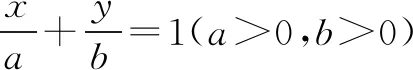
变式6(2012浙江文)若正数x，y满足x+3y=5xy，则3x+4y的最小值是( ).

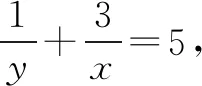
由课本习题的解题过程出发，结合变式在高考中呈现方式，命制出这样一个题目.

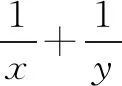
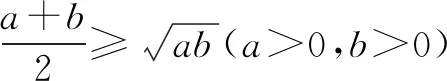
此题与上面课本习题有着千丝万缕的联系，当然有很多相似的解法，要提高难度，只需进行变式.比如将条件等价变形，清除原来的痕迹，或将条件变换，使其看不清实质条件，还可以改变设问方式，这样增加难度.

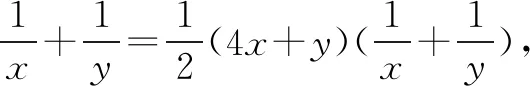
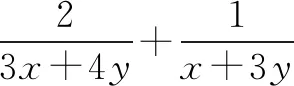
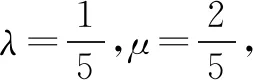
三、一点思考

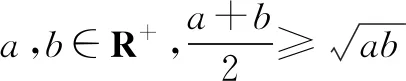
命制试题要专研教材与高考题，厘清思路，形成自己的体会，比如从一道不等式的高考题出发，看看命制优秀试题心路历程.

A.1 B.2 C.3 D.4

课本上(人教版《数学》第二册上(2004版)复习参考题六B组第33页第3题)

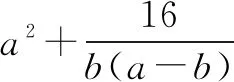
答案：D

命制试题能够极大地提升教师理解教材，运用教材的能力，同时学生在解决这些具有针对性的问题时，落实核心素养.