乱花渐欲迷人眼 拨开云雾见分明——浅析基本不等式的变形与应用

张 斌

(陕西省渭南市韩城市西庄中学 715403)

一、基本不等式的三种应用

基本不等式的常见变形式如下：

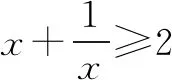
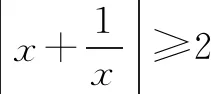
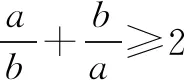
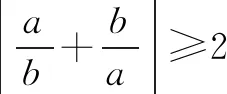
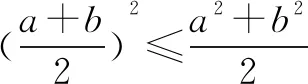
提示(1)当两个正数的积为定植时，可以求它们的和的最小值.当两个正数的和为定植时，可以求它们的积的最小值.正所谓“积定和最小，和定积最大”.

(2)求最值的条件“一正，二定，三取等”.

(3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用.

应用一：求最值

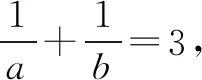
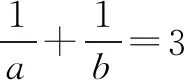
应用二：基本不等式与恒成立问题

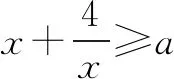
A. (-∞,5] B. (-∞,4]

C. (-∞,2] D. (-∞,1]

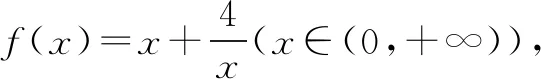
应用三：均值定理在比较大小中的应用

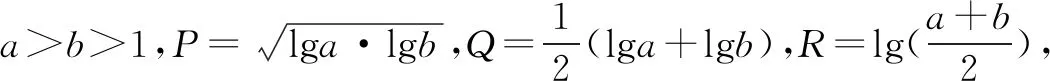
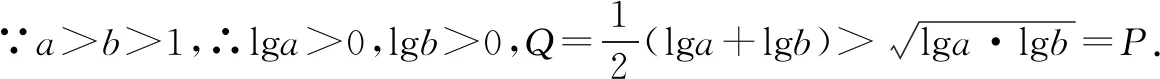
∴R>Q>P.

二、应用基本不等式的八种变形技巧

基本不等式的一个主要功能就是求两个正变量和与积的最值，即所谓“和定积最大，积定和最小”.但有的题目需要利用基本不等式的变形式求最值，有的需要对待求式作适当变形后才可求最值.常见的变形技巧有以下几种：

1.加上一个数或减去一个数使和或积为定值

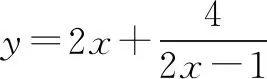
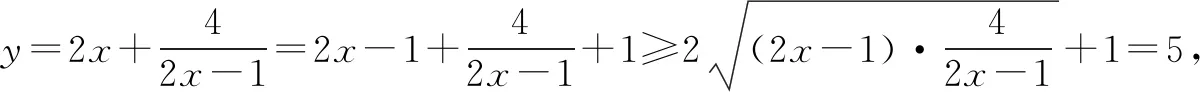
2.平方后再使用基本不等式

一般地，含有根式的最值问题，首先考虑平方后求最值.

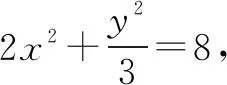
点拨由于已知条件式中有关x，y的式子均为平方式，而所求式中x是一次的，且根号下y是二次的，因此考虑平方后求其最值.

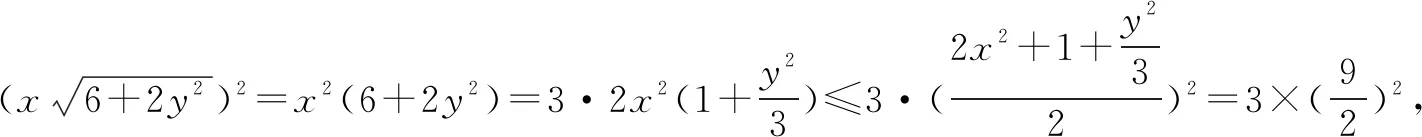
3.展开后求最值

对于求多项式积的形式的最值，可以考虑展开后求其最值.

例6 若实数a，b满足ab-4a-b+1=0(a>1)，则(a+1)(b+2)的最小值为____.

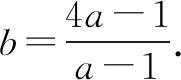
4.变形后使用基本不等式

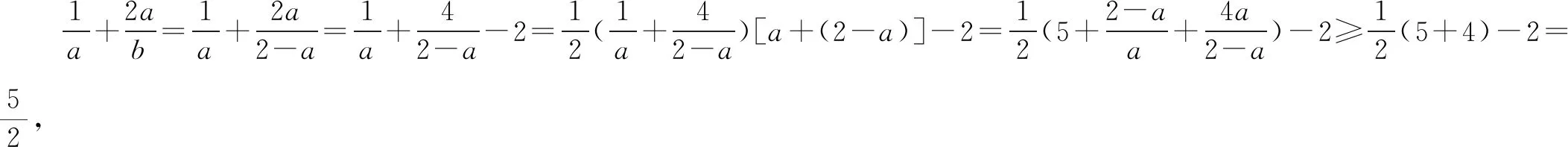
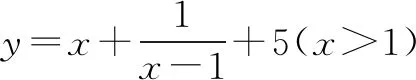
A.5 B.6 C.7 D.8

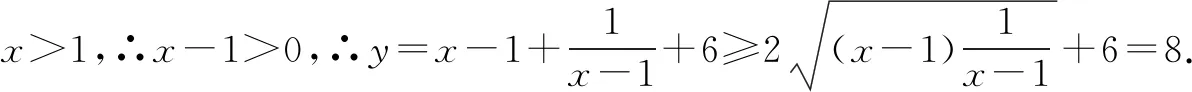
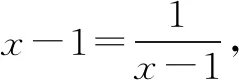
6.用“1”的代换法求最值

A.3 B.4 C.5 D.6

7.代换减元求最值

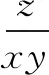
点评在含有两个以上变元的最值问题中，通过代换的方法减少变元，把问题化为两个变元的问题使用基本不等式，或者把问题化为一个变元的问题使用函数方法求解.

8.建立求解目标不等式求最值

例11 已知x，y均为正实数，且xy=x+y+3，则xy的最小值为____.

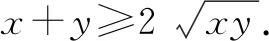
利用基本不等式与已知条件建立求解目标的不等式，求出不等式的解集即得求解目标的最值.

三、基本不等式的应用

欧拉是一位家喻户晓的数学家，有惊人的数学才能和数学发现，以他名字命名的有欧拉定理、欧拉公式、欧拉线等.当然也有许多美丽的传说，小时候帮父亲解决了一个棘手的问题：

例12因羊繁殖增多，他父亲计划建一个长40米，宽15米共600平方米的长方形羊圈.可动工时才发现原有的材料只够围100米的篱笆，该如何办？正在为难时，小欧拉给了一个建议，把羊圈建成一个边长为25米的正方形.父亲照着小欧拉设计扎了一个正方形的羊圈，100米长的篱笆真的够了，面积还比原来的稍大一些.这是为什么？如何解释欧拉的设计？

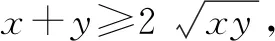
事实上，欧拉总结出一条规律：在等周长的矩形中，正方形的面积最大.

例13港珠澳大桥通车后，经常往来于珠港澳三地的刘先生采用自驾出行.由于燃油的价格有升也有降，现刘先生有两种加油方案，第一种方案：每次均加30升的燃油；第二种方案，每次加200元的燃油，则下列说法正确的是( ).

A.采用第一种方案划算 B.采用第二种方案划算

C.两种方案一样 D.无法确定

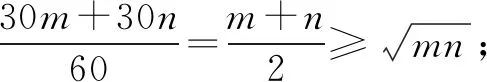
所以无论油价如何变化，第二种都更划算.故选B.

陶行知老先生曾经说过：“生活主义包含万状，凡人生一切所需皆属之.”生活就是教育的本源，生活中所产生的实际问题，便是教育的沃土.教育的出发点正是为了解决生活中的一切问题而产生的.在解决问题中理解和学习知识，才是真正的“知行合一”.