对一道高考不等式的思路探究与推广

纪定春

(四川师范大学数学科学学院 610068)

2019年高考数学全国卷Ⅰ理科第23题，该试题为条件不等式问题，同时是一道具有数学探究价值的不等式试题.从多个角度对该试题进行思路探究，能够激活学生的数学思维;对试题进行推广，能够培育学生的创新意识，进而提升学生的一般性思维策略，优化数学思维品质.

一、试题的呈现与评注

设a，b，c为正数，且满足abc=1.证明：

(2)(a+b)3+(b+c)3+(c+a)3≥24.

评注该试题结构简单、形式对称，给人以数学美的感受.此题具有深刻的数学内涵、思维面开阔、切入点多、解题思路丰富等特点，能够满足不同考生的解题需要，体现了高考对考生的人文关怀，是一道优秀的高考不等式试题.该题目的问题设计具有层次感，可以适当地提高考生的区分度.因此，这是一道值得探究的好试题，接下将从不同角度，对该试题进行思路探究，并将该试题进行推广.

二、试题的思路分析与探究

1.对问题(1)的思路探究

思路1分析法

综合法和分析法是常见的数学解题思路分析和探究方法.分析法是一种“执果索因”的思维分析方式，而综合法是从原因(条件)出发去寻找结果(结论).可见，两种分析方法恰好是一个互逆的思维过程.

解析题设a，b，c为正数，且满足abc=1.

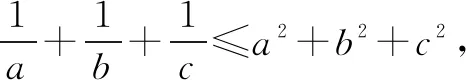
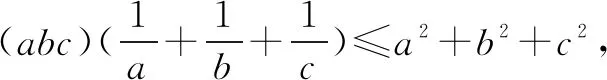
需证bc+ac+ab≤a2+b2+c2，

需证a2+b2+c2-bc-ac-ab≥0，

需证(a-b)2+(b-c)2+(c-a)2≥0.

显然该不等式成立.取等条件为“a=b=c=1”.(注：以下均不再指明取等条件)所以原不等式得证.

评注此方法巧用条件“abc=1”，将不等式的的左端的分式结构化为整式结构.综合法实质上是一种逆向思维的方法，通过结论来找出上一步成立的必要条件.因此，可以借用此方法来培育学生的逆向思维能力.

思路2基本不等式法

根据辞海的解释，基本是指根本、基础的.可见，基本不等式是相较于重要不等式更为基础的不等式，也是最根本的不等式，通过基本不等式可以推导其它重要不等式.故将a2≥0规定为“基本”不等式，可以发现这个不等式是没法证明的.由基本不等式a2≥0出发，可以推导出几何不等式、算术不等式、均值不等式、幂不等式、柯西不等式、伯努利不等式等，可见这个规定是合情理的.

解析由abc=1，将不等式两边同时乘以“abc”，转化为bc+ac+ab≤a2+b2+c2.

则原问题等价为证明a2+b2+c2-ab-bc-ca≥0.

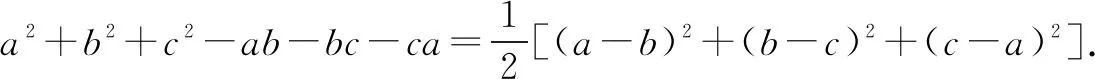
由基本不等式，可知(a-b)2≥0，(b-c)2≥0，(c-a)2≥0.

所以a2+b2+c2-ab-bc-ca≥0.

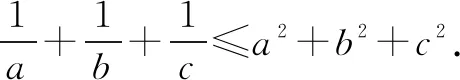
评注该方法先用“abc=1”，将问题中的分式不等式转化为整式不等式，然后巧用“配凑”恒等变形，最后用基本不等式来解决，充分体现了化归与转化思想.

思路3重要不等式法

重要不等式，是比基本不等式更加广泛的不等式，是指向的一大类不等式，如绝对值不等式、三角不等式、对数不等式、指数不等式、柯西不等式、伯努利不等式、权方和不等式、排序不等式等.不等式一般是用来解决最值的一种方法，如求最大值、最小值等.

解析由abc=1，将等式两边同时乘以“abc”，可得bc+ac+ab≤a2+b2+c2.

由重要不等式，可知a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca.这三个同向不等式相加，则有a2+b2+c2≥ab+bc+ca.

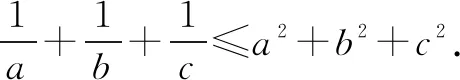
评注该方法巧借不等式的对称结构和不等式的加法性质，建立了二元均值不等式与所证不等式之间的联系，体现了由局部到整体、对称和轮换等思想.

思路4向量法

向量是具有大小和方向的量，是一种矢量.向量的引入，将无向的几何带上了方向和大小，这对几何的研究是方便的、进步的.向量法，是一种利用向量的性质、运算等解决问题的一种方法.向量在高中应用广泛，如求线面角、面面角、线线角、距离、最值等.

解析借助abc=1，先将待证式的左边化为整式，即证明a2+b2+c2≥ab+bc+ca.

设向量m=(a,b,c)，n=(b,c,a).

因为|m||n|≥|m·n|，所以有

可得a2+b2+c2≥bc+ac+ab.

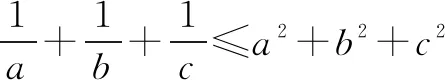
评注该方法巧设m=(a,b,c)、n=(b,c,a)这两个向量，这样才能够使得两个向量相乘恰好等于“ab+bc+ca”.这样的巧设法体现了轮换和对称的数学思想，值得细细品味.显然可以看出，这里的两个向量的设法是不唯一的.

思路5柯西不等式法

柯西不等式是高中数学选讲的内容，是一个容易被忽略的知识点，但却是高考的一个热门考点知识，尤其是在中学数学竞赛中时常使用.柯西不等式，即对任意的实数a，b，c，d，e，f，有不等式(a2+b2+c2)(d2+e2+f2)≥(ad+be+cf)2成立.

解析由a，b，c为正数，且满足abc=1.

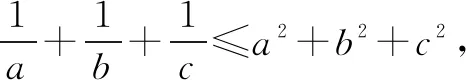
于是，等价于证明a2+b2+c2≥bc+ac+ab.

将两边同时平方，上式等价于(a2+b2+c2)2≥(bc+ac+ab)2，

也即(b2+a2+c2)(c2+b2+a2)≥(bc+ab+ca)2.

由柯西不等式可知，上述不等式成立，故原不等式成立.

评注柯西不等式是解决多元不等式最值问题的好方法，首先要将问题转化为(或配凑)柯西不等式的结构形式，然后再利用柯西不等式来判断.

思路6排序不等式法

排序不等式，指在一列规定了大小顺序的数字或字母，将它们按照一定的次序相互作用(相乘组合)，会产生不同大小结果.通常情况下，结论为：顺序和≥乱序和≥倒序和.

解析已知a，b，c为正实数，不妨假设三者满足关系a≥b≥c>0.

由排序不等式可知，顺序和≥乱序和，则a·a+b·b+c·c≥a·b+b·c+c·a.

即不等式a2+b2+c2≥ab+bc+ca成立.

评注排序不等式是一种重要的不等式，在中学数学竞赛中占有十分重要的地位，应该值得关注.

思路7“Δ”判别法

判别式法，是一种二次函数中判断函数零点(实数范围内)是否存在的一种方法.判别式法在几何、代数中具有广泛的应用价值，是一种重要的数学方法.

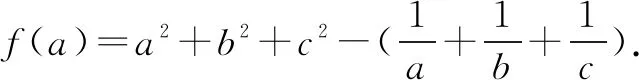
由abc=1，可得f(a)=a2+b2+c2-bc-ac-ab

=a2-(b+c)a+b2+c2-bc.

则Δ=(b+c)2-4(b2+c2-bc)

=-3(b2+c2)+6bc≤-3·2bc+6bc=0,

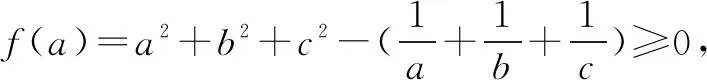
评注该方法是解决二次不等式恒成立问题常用的方法.注意，这是一个关于a，b，c的对称结构，故a，b，c在不等式中的地位是等价的，故任意选择一个当主变元均可.

思路8二次函数法

克莱因说“函数是数学的灵魂.”函数是研究数集(或变量与变量)之间对应关系的数学模型.函数与方程、不等式、数列、几何、概率等之间存在紧密的联系.函数在研究连续变量和离散型变量中发挥着重要的作用，现行高中数学知识体系，始终以函数为主线，贯穿其中，这就充分地体现了函数的重要地位和价值.二次函数作为中学数学中一类重要的函数模型，对研究函数的最值问题，有着极为独特的地位和作用.

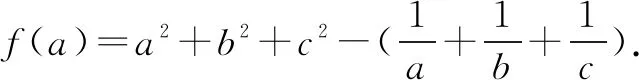
由abc=1，可得f(a)=a2-(b+c)a+b2+c2-bc.

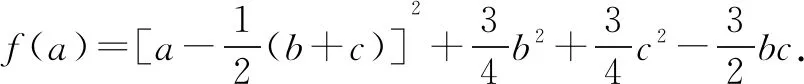
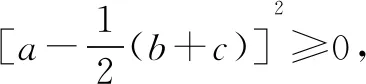
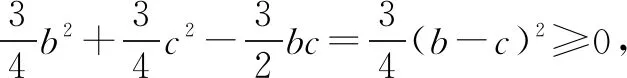
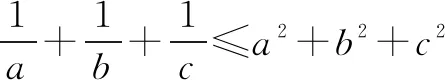
评注该方法创造性地使用二次函数性质，将不等式问题转化为函数最值问题解决.

思路9导数法

导数是沟通初等数学和高等数学的一座重要桥梁.导数法，就是利用导数的知识和方法来研究问题的方法，特别是在研究函数的单调性、最值点、极值点、凹凸性等方面具有广泛的应用.因此，高中数学应该重视导数的教学.

解析略.

评注导数法可视为对思路9的优化，可用导数来研究函数f(a)单调性和最值，此处不再给出具体的证明过程.

2.对问题(2)的思路探究

思路1重要不等式法

解析由题知，这是一个三元不等式恒成立问题，考虑用三元均值不等式法.因此，有

(a+b)3+(b+c)3+(c+a)3

=3(a+b)·(b+c)·(c+a).

此处再考虑使用3个二元均值不等式，则

3(a+b)·(b+c)·(c+a)

故不等式(a+b)3+(b+c)3+(c+a)3≥24成立.

评注通过观察该试题的结构形式，为3项且每项的次数为3，自然想到可以用三元均值不等式，这样放缩以后就不会产生根号.经过第一次的放缩显然是不够的，还需要使用二元均值不等式再次进行放缩，才可将放缩结果与条件“abc=1”联系起来.

思路2权方和不等式法

权方和不等式是一个重要的不等式，它完美地将柯西不等式和变异形式的柯西不等式统一起来，是解决高次分式型不等式最值的重要工具，在竞赛数学中具有广泛的应用.

权方和不等式，即设ai，bi>0，i=1，2，…，n，k∈N*，则成立不等式

解析由题意知，有(a+b)3+(b+c)3+(c+a)3

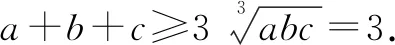
故(a+b)3+(b+c)3+(c+a)3

评注权方和不等式的优势，在于能够有效的解决分式型高次求和最值问题，题目中提供的条件“abc=1”恰好可以与“a+b+c=1”建立起联系，所以用该方法解决这类试题会更加简洁有效.

三、问题的推广

张景中院士曾经指出：“推广是数学研究中极重要的手段之一，数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上，向未知的领域扩展，从实际的概念及问题中推广出各种各样的新概念、新问题.”将一个数学问题推广，可以使得该问题在更大的范围内成立.数学自身的发展是离不开数学问题的推广的.数学问题的推广过程，其实也是在培养学生数学创新意识的过程，这更是一个从已知到未知的过程，需要充分地激活大脑的数学思维.接下来，对试题进行推广.

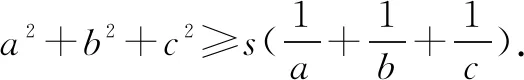
评注推广1是将试题的条件推广到更一般的情况，可以通过改变“abc=s”，来进行试题的命制和改编.

推广2设a，b，c为正数，且abc=s,k∈N*.求证：ak+bk≥3sk/3.

评注推广2，将次数和条件“abc=1”同时进行了一般化处理，使得在更一般的条件下试题可以成立，可以使用权方和不等式进行解决，此处不再具体给出过程.

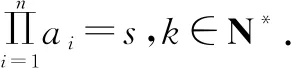
评注推广3是在推广2的基础之上，将项的个数进行了推广，解决方法同推广2.

推广4 设a，b，c，d为正数，且abcd=1.求证：

(a+b)4+(b+c)4+(c+d)4+(d+a)4≥64.

评注推广4将问题(2)项数和次数增加了1，解决方法可以类比问题(2)，这个推广比较简单，可以考虑纳入数学课堂练习.

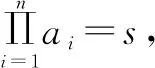
评注需要注意，所求解不等式左边是一个循环结构，求解时需要注意项的个数.

以上推广，可以根据学生的实际情况，有选择地将上述推广纳入数学课堂教学.