“黑三角”噪声特征分析及压制
张力起,刘亚辉,王华忠
(1.同济大学海洋与地球科学学院波现象与智能反演成像研究组,上海200092;2.南方海洋科学与工程广东省实验室(湛江),广东湛江524088;3.中国石油大学(华东)地球科学与技术学院,山东青岛266580)
陆上油气勘探是我国油气勘探的重点区域,尤其是中西部复杂地表区域更是我国油气勘探的战略接替区域。但是,复杂的地表条件(地表高程和介质岩性变化大)以及震源和检波器与复杂地表介质的相互作用,导致陆上油气勘探的复杂化,尤其是地震数据的信噪比急剧降低,严重影响了地震波成像质量,成为我国中西部探区高精度油气勘探的重大瓶颈之一。
炸药震源和可控震源与复杂地表介质的相互作用,产生了复杂的、在近地表传播的波现象。这些波现象很难或不利于中深层的地震波成像,成为了严重的干扰波。一般认为:复杂的瑞雷型面波、直达波、折射波、反射波及散射波等构成了近地表区域传播的主要波场。由于不同探区地表介质情况不同,近地表区域传播的主导波场也存在明显差异,这可以从不同地区采集的单炮道集噪声的显著变化观察到。此外,这些在近地表传播的“噪声”波场的能量占震源激发总能量的90%以上。依据地表条件的不同,它们沿着偏移距和时间方向的衰减情况变化很大。但总体而言,在浅层小偏移距、中深层大偏移距范围内衰减较慢,并且大部分的记录时间内(一般为6s)都会出现这些“噪声”波场。
真正复杂的还不是这些“噪声”波场在单炮道集中的大范围出现,而是它们所具有的复杂多变的特征,使得目前的信号处理理论和方法难以适用于这些特征,不易发展出有效的滤波器来压制这些“噪声”波场。
“黑三角”噪声是目前较难解决的问题之一。尤其是沙漠地区可控震源采集的单炮地震数据,以瑞雷型面波和面波散射波为主形成的“黑三角”噪声,在三维情形下主要分布于以炮点位置为顶点的锥形体内。“黑三角”噪声中所包含的线性性比较强的地滚波具有强振幅、低频、低视速度、频散等特征[1],除此之外的其它波现象还具有异常强振幅、短同相轴展布、中低频分布等特征。当地表低速层厚度较大,采用可控震源激发获得的单炮道集中,“黑三角”噪声变化异常显著,且其覆盖面积在某些情况下可以占单炮道集总面积的一半左右,这严重降低了单炮道集及其成像结果的质量。一般地,针对“黑三角”噪声中线性性比较强的地滚波存在有效的压制方法。DEIGHAN等[2]在Wavelet域、NAGHIZADEH等[3]在Curvelet域利用信号在不同尺度和方向上的特征设计滤波器进行信号预测从而压制地滚波。基于地滚波的强振幅以及线性特征,LIU[4]使用Karhunen-Loeve变换、CHIU等[5]基于特征图像提取方法在局部时空窗内构建相干噪声模型,并对输入数据采用自适应方法来衰减地滚波。LI等[6]利用目前比较前沿的卷积神经网络(CNN)对地滚波进行学习来预测“黑三角”噪声。具有线性特征的地滚波经过径向道变换(radial trace transform,RTT)后呈现低频特征,基于低通滤波器可以实现对地滚波的压制[7-10]。
“黑三角”噪声的特征比一般地滚波更为复杂,并且随地表条件的不同,采集的数据特征差异也很显著。因此需要发展一种依据数据特征而设计的组合滤波方法。本文首先分析“黑三角”噪声的特征,提出了数据自适应的噪声压制组合方案,最后对实际采集的地震数据进行处理,以验证该方法的有效性。
1 地震数据去噪的理论基础
对含有噪声的地震数据进行噪声压制的根本问题在于能否预测数据中蕴含的信号。首先要建立一个描述数据的模型。地震波场可以表达成信号、相干噪声和随机噪声3部分的叠加,可记为:
u(x,y,t)=S(x,y,t)+ηC(x,y,t)+ηR(x,y,t)
(1)
式中:u(x,y,t)为观测数据;S(x,y,t)为待处理的地震信号;ηC(x,y,t)为相干噪声;ηR(x,y,t)为满足一定概率分布的随机噪声。地震信号分析的基本思想是将含有噪声的信号视为Hilbert空间中的一个平方可积函数,选取合适的基函数进行信号稀疏的、近似的表达(信号预测的正问题);然后在一定的估计理论基础上,基于上述信号预测的正问题,求解最佳的信号预测器,从而实现信号的最佳估计。显然,这是一个典型的Hilbert空间中的函数逼近问题。在此理论框架下,地震数据的去噪、插值、压缩和特征提取等处理过程可以统一起来。
实测地震数据波场中包含的信号、相干噪声是可预测的,是确定性信号。对确定性信号(连续函数)进行预测,本质上是在Hilbert空间中寻找一组基函数,在L2范数意义(也可在其它范数意义)下达到逼近误差最小,以实现函数的最佳逼近。随机噪声只能从概率或统计的角度进行预测,即利用联合概率密度函数或联合概率密度函数计算出的某种统计量来预测。统计意义下建立上述信号模型中噪声满足的概率分布模型,是对信号进行建模的另一种重要方法。在地震勘探中,最基本的随机噪声类型主要有两类:满足Gauss分布(包括广义Gauss分布)和满足脉冲分布。噪声ηR(x,y,t)满足Gauss分布的前提条件是对数据中的相干信号(包括相干噪声)进行准确的预测。
高维统计滤波[11]和基于Hilbert空间中函数逼近进行信号预测的滤波本质上相同,如各向异性Gauss滤波器与Gauss线性滤波器本质上是一致的。总之,对实测数据中包含的信号(包括相干噪声)进行最佳预测是噪声压制的根本思想。
2 “黑三角”噪声特征分析
信号模型的建立和基于此模型的滤波方法的构建都是建立在对数据中信号和噪声特征进行深入分析的基础上。“黑三角”噪声的特征复杂,炮集之间特征变化快,只有很好地理解“黑三角”噪声的特征才能设计出合适的滤波器组合。
在复杂地表(地表起伏、存在低速层,常见于沙漠地区)以及不同的激发条件下(主要是可控震源),“黑三角”噪声主要是由瑞雷型面波和面波散射波组成,三维地震数据中这些噪声主要分布于以炮点位置为顶点的锥形体内。不同探区的地表条件会造成在地震数据采集过程中出现特征不同的“黑三角”噪声。事实上,同一探区内,不同炮集之间“黑三角”噪声也不相同。
图1a为某工区可控震源采集的单炮记录;图1b为0~30Hz频率扫描的信号,占总能量的47.68%;图1c 为30~80Hz频率扫描的信号,占总能量的50.83%。图1d为对图1a数据进行线性动校正后的结果(v=600m/s),可以观察到不同倾斜角度的线性同相轴(红色圈所示)和异常强噪声(黄色圈所示),因采样不足引起的空间假频显著降低,同相轴线性性显著增强,有利于设计最佳线性预测滤波器去除这些线性噪声。图1e和图1f分别为图1a第34道和第48道经过S变换[12]的时频谱,可以看出,低频(0~30Hz)成分在“黑三角”噪声区域(图1a绿色线以下部分)内都有分布,而中高频成分(30~80Hz)只分布在中浅层,且能量占比很高。
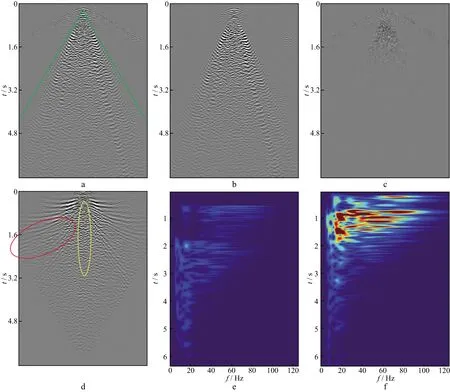
图1 某工区可控震源单炮记录及分频扫描结果
图2a为另一工区炸药震源采集的单炮记录;图2b 为0~30Hz频率扫描的信号,占总能量的79.4%;图2c为30~80Hz频率扫描的信号,占总能量的20.28%;图2d为对图2a数据进行线性动校正后的结果(v=600m/s);图2e和图2f分别为图2a第228道和第260道经过S变换的时频谱。图2a与图1a数据特征相差甚远,图2a道集能量主要分布于低频端(图2e、图2f),中深层的散射波较强并且存在少量线性地滚波(图2d)。但总体上,“黑三角”噪声在时、空、频3个域中的特征与图1的分析基本保持一致。
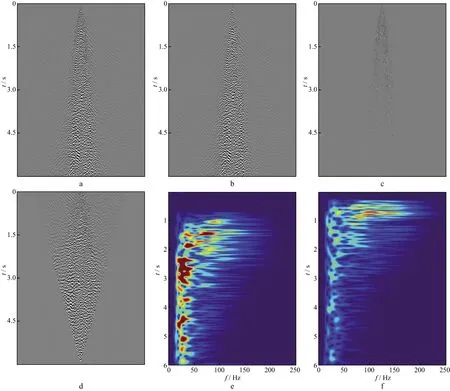
图2 某工区炸药震源单炮记录及分频扫描结果
“黑三角”噪声的特征在不同探区以及在同一探区的不同近地表条件下(地表起伏程度、低速层速度及厚度等)都有较大变化,可控震源和炸药震源激发采集的炮集中“黑三角”噪声的波场复杂程度也不尽相同。无论如何,有效的去噪方法都需要建立在对噪声特征的正确认识基础之上。
3 “黑三角”噪声压制方案
根据前文对信号预测和去噪方法的基础理论分析以及对“黑三角”噪声的特征分析,可以总结出以下结论:不存在一个单一的去噪方法能有效压制“黑三角”噪声,需要一个组合去噪方案,包含针对不同噪声特征的多种去噪技术。
“黑三角”噪声特征可概括为:噪声主要分布在比较明显的三角区域、强振幅短同相轴展布、孤立强振幅反射(若干个强幅值地震子波组合)、低频成分占优、低速、频散、异常强噪声出现在中浅层等。据此提出如下基于自适应数据变化特征的“黑三角”噪声压制方案。
1) 设计简单的图像区域分割算法或利用高级的机器学习算法,划分“黑三角”噪声区域。
2) 为改善“黑三角”区域中相干噪声和相干信号的线性性,降低由于采样不足引起的频散对同相轴线性性的影响,选择一定的视速度进行动校正。
3) 设计合适的窗函数,在局部时空窗内对数据进行线性信号的预测。选择数据窗大小和一定频率段,设计f-x-y域最佳预测滤波器或者稳健主成分分析(robust principal component analysis,RPCA)线性信号预测器,压制线性噪声。
4) 设计中值滤波器,压制异常点(强)噪声。
4 “黑三角”噪声压制方案中的关键方法技术
如前文所述,“黑三角”噪声压制方案中,包含若干项关键方法技术。下面仅重点简述两项:线性动校正和RPCA线性预测。
4.1 根据视速度进行线性动校正
“黑三角”噪声主要分布在一定视速度范围的锥形体内,由于地震数据空间采样稀疏,假频相当严重,如图3a红色椭圆框所示。为了提高“黑三角”区域中相干噪声的线性性以及与相干信号的可分离性,降低频散对线性同相轴的影响,根据“黑三角”噪声区域内最大视速度进行动校正是很必要的步骤。
图3a是实际单炮数据,图3b是对应的线性动校正后的结果。由图3可以看出,线性动校正后显著改善了相干噪声的假频特征,提升了线性特征,为后续的线性噪声预测提供了更好的基础数据。

图3 实际地震数据(a)和线性动校正后的结果(b)
4.2 局部时间空间窗内RPCA线性信号预测
在分频滑动时窗内进行线性噪声预测是本文提出的“黑三角”噪声压制方案中的核心环节。局部窗内的线性预测可以有多种实现方法,如f-x域预测器、各向异性Gauss滤波器、各种小波变换理论下的滤波器。我们认为,针对“黑三角”噪声,先进的线性信号预测器不是最根本的,适应噪声统计特征的信号预测器才是所需要的。我们采用RPCA方法提取线性相干噪声。
给定一个数据矩阵D∈Rm×n,当数据是由低秩部分和稀疏部分(噪声满足Laplace分布)构成时,可以建立如下模型:
D=A+E
(2)
其中,A和E分别表示低秩数据和稀疏数据。
为了求解上述问题,建立如下目标泛函:
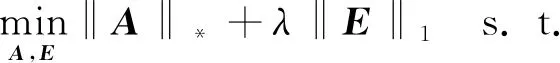
(3)
其中,‖·‖*为核范数,‖·‖1表示L1范数,λ为正加权参数。
对于公式(3),其增广拉格朗日函数为:
(4)
LIN等[13]提出了求解公式(4)的增广拉格朗日乘子方法。但当E不满足稀疏性要求时,需要精细选择λ的取值,才能获得精确的解。为了解决上述问题,LEOW等[14]提出了固定秩的稳健主成分分析(fixed-rank robust principal component analysis,Fr-RPCA)方法,即认为矩阵A的秩r已知:
(5)
公式(5)的求解算法如图4所示。

图4 公式(5)的求解算法
图中,J(X)=max(‖X‖2,λ-1‖X‖∞),
图5展示了采用RPCA方法对图3b数据进行相干噪声预测以及线性反动校正后的结果。对比图3a 和图5b可以看出,带假频的大部分相干噪声被提取出来。去除这些噪声可以在很大程度上压制“黑三角”噪声。

图5 采用RPCA方法对图3b数据进行相干噪声预测(a)以及线性反动校正(b)后的结果
5 实际资料测试
图6a所示为某工区实际采集的单炮记录;图6b 是采用本文方法提取出的相干噪声。由图6a和图6b可以看出,大部分相干噪声被提取出来。最终滤波结果(图6c)中已经有反射同相轴显现出来。

图6 某工区实际采集的单炮记录(a)、采用本文方法提取出的相干噪声(b)以及最终滤波结果(c)
该实际资料应用结果表明,本文提出的“黑三角”噪声压制方案可行,所使用的关键技术组合有效。本文主要对“黑三角”噪声中相干噪声以及异常强振幅噪声的压制进行了研究,后续将在既定的方案下,通过实验和对比选择更合适的技术组合,达到对“黑三角”噪声更理想的压制效果。
6 结论及讨论
复杂的地表介质与可控震源及炸药震源相互作用引起的在近地表传播的复杂波场形成噪声,严重干扰地震波成像质量,成为了此类工区高精度油气地震勘探的瓶颈。“黑三角”噪声就是一个典型问题。基于对“黑三角”噪声的特征分析以及压制方法研究,本文提出了一种依据数据特征而设计的滤波方法。实验结果显示了该方法能够有效压制线性相干噪声以及部分异常强振幅噪声并保留有效反射信号。但该方法依旧存在一些不足之处,例如炮点附近异常噪声压制不完全,深层仍有部分噪声存在等,需要进一步改进。
客观地讲,本文提出的方法技术仅仅是依据目前对已有的“黑三角”噪声单炮记录进行噪声特征分析后提出的初步研究成果。但由于收集到的数据有限,“黑三角”噪声特征的分析不全面,去噪方案中涉及到的方法技术也有不足之处。
通过对“黑三角”噪声的压制方案和方法技术的研究,初步发现其特征很复杂,在空间和时间上变化也很快,彻底压制几乎不可能。我们认为:基于统计滤波的思想,发展出数据自适应的滤波方法,是合理的技术发展逻辑。这也是当前基于统计学习方法进行智能去噪的发展方向。
致谢:感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中国石化石油物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。

