高效采集中的随机地震观测系统设计及数据重建
吴 涛,徐 鹏,冯 波,4
(1.中海石油(中国)有限公司湛江分公司,广东湛江524057;2.南方海洋科学与工程广东省实验室(湛江),广东湛江524088;3.同济大学海洋与地球科学学院波现象与智能反演成像研究组,上海200092;4.同济大学海洋高等研究院,上海200092)
地震数据采集是油气地震勘探的核心环节,地震波成像质量的改善、地震地质解释精度的提高,乃至油气勘探效益的提高,都建立在采集的高品质地震数据的基础上。目前,地震数据采集理论和技术进展主要体现在两个方面:一是采样理论从Shannon采样[1-2]发展到压缩感知(CS)采样[3-9];二是“两宽一高”地震数据采集[10-16]成为导向性的数据采集技术。
从数据采样理论看,Shannon采样定理解释了如何进行规则离散采样才能完整地恢复成连续数据,而压缩感知采样建立了一套由随机离散采样数据恢复成连续数据的理论,它要求数据在某种变换域表现为稀疏特征。对于地震数据,多次覆盖的观测系统使得地震信号表现出高维空间特征。不同于仅关注一维信号特征的Shannon采样定理,高维地震信号的空间结构取决于地下地质结构的复杂程度,如平缓层状地层中的地震波场相比复杂断块区的地震波场更加简单,稀疏特征更明显。
当前的高效采集更多地关注多炮激发的采集方式,强调激发时间的随机,而空间随机采样更多地关注炮点和检波点的空间随机布设。前者更多地关注单位时间内的炮数,主要关注采集效率,后者更多地关注炮数、检波线数及检波点点数,能够更好地实现空间随机采样。
空间随机采样原则上主要关注炮点和检波点如何随机布设才能以更高精度恢复成规则无假频数据体。地震波场的空间结构越简单,空间随机采样的数据恢复成规则无假频数据体时越容易,对应地,在空间随机采样时,采样间隔越稀疏。因此,随机采样与地下地质结构的复杂程度有关,与压缩感知理论要求信号具有稀疏特征完全一致。然而,目前地震数据压缩感知采样尚未将随机采样方式的设计与地下介质复杂度以及与之对应的波场复杂度关联在一起。
截至目前,随机采样观测系统的设计依然缺乏明确的理论指导,噪声严重限制了数据恢复的精确度,静校正量破坏了信号的稀疏性,这些都影响了随机采样的实用性。地下介质的复杂导致波场(信号)复杂,信号的可稀疏表达性下降,也限制了随机采样的应用。上述几方面的原因,导致目前陆上起伏地表和地下复杂探区随机采样的应用非常谨慎。海上进行空间随机采样的条件优于陆上。总之,随机采样(尤其是空间随机采样)具体应用时面临很多限制条件。
因此,不能单纯地从降低采集成本的角度理解空间随机采样,这样会导致压缩感知随机采样的误用或滥用。我们认为,在同等投资条件下,相较于均匀采样,随机采样或许可以更好地感知反射波和绕射波信号的存在。利用更少的采样获得更多的信息,才是压缩感知随机采样的真正价值。压缩感知随机采样的目的不是为了减少炮点和检波点(从而降低成本)的稀疏采样,相反地,其目标是以可接受的成本实现更高要求的“两宽一高”采样。
尽管仍存在诸多问题,但在地表条件和地下构造不复杂的探区以及工农业发达的油气探区,随机采样技术是有其应用价值的。本文重点讨论炮检空间随机观测系统的设计理念,并以合成数据进行验证。
1 随机观测系统设计的基本理念
压缩感知数据重建可以描述为如下压缩感知反演问题:
(1)
式中:A为一定基函数(族)形成的稀疏变换(矩阵);Sreg为期望采集到的规则数据;‖·‖p表示某种范数,p可取0或1,也可拓展为矩阵核范数;Q为随机采样算子,勘探地震中即随机观测方式;Sobs为实际测量的随机观测数据。
根据压缩感知理论,若信号即道集中的同相轴具有局部稀疏性或在变换域表现为稀疏性,通过选择合适的稀疏变换及随机采样(不相干的),可以用较少的空间随机采样重构连续信号,实际上是规则无假频的地震道。事实上,观测波场的(局部)稀疏性、空间随机采样感知具有局部稀疏性的波场、空间随机采样数据恢复成用于后续成像处理的规则无假频数据体是三位一体的。
然而,利用压缩感知理论精确恢复规则无假频信号与高维地震信号(地震波场)的结构特征(或空间复杂度)以及地下地质结构密切相关。对于平缓层状地层,地震信号相对简单,空间随机采样可以相对稀疏。反之,对于复杂地震信号,其稀疏度显著下降,因而需要更密的空间随机采样。
野外观测的地震数据既含有外源性噪声(如各种震动和工业电干扰等)又含有与地表相关的噪声,地表条件越复杂,噪声越强。同时,地表高程变化会导致道间时差、近地表或地下介质非均匀性会产生道间静校正量,它们会使得地震信号的复杂度显著升高,大大降低了地震信号的稀疏性。因此,在实际应用中,随机观测数据恢复成规则无假频数据仍然存在较大的难度。
Shannon规则采样可以定义一个不产生假频的Nyquist频率(波数)并计算时间(空间)采样率,然后进行野外地震数据采集。空间随机采样则必须用规则无假频数据的恢复精度作为评估观测系统设计合理性的指标。但是在复杂波场加强噪声情形下,规则无假频数据的恢复仍存在很大困难。
据此,可以利用地震道集中的特征波,如初至波、线性面波或标志性反射波,其特征更容易描述,因而更容易实现稀疏表达,更方便进行规则无假频数据的恢复,用于评价空间随机观测系统的合适程度。更重要的是,特定探区这些特征波现象比较稳定,只要这些特征波现象能够得到高精度恢复,就可以认为空间随机观测系统的设计是合理的。这种设计理念用于地表条件简单的工区无大碍,但由于真正实现空间随机观测系统的合理设计需要考虑的因素很多,因此我们提出的理念也是一种权宜之计。
2 炮检点空间位置随机的观测系统设计方法
由压缩感知理论可知,随机采样算子要满足有限等距性质(RIP),即随机采样算子必须满足对理想规则无假频数据进行高斯随机采样的条件。如此采样才能在压缩感知理论下更好地恢复规则无假频数据,并用数据恢复的精度评价空间随机观测系统设计是否合适。据此,我们提出了炮检随机观测系统设计方法应满足的基本条件,即高密度地震数据采集(或常规地震数据采集)观测系统建立的基础网格,既控制了面元内覆盖次数、方位角和偏移距的均匀程度,也决定了随机采样观测系统野外施工的方便程度。空间随机的观测系统设计在已有的高密度地震数据采集(或常规地震数据采集)观测系统上进行是必要的约束条件。
随机采样观测系统设计的原则是在高密度地震数据采集(或常规地震数据采集)观测系统建立的基础网格基础上,按照高斯随机采样的理论要求,把规则欠采样的网格作为高斯随机采样位置的期望,同时以允许的高斯抖动最大距离的1/3作为标准差,分别在炮集上进行空间随机检波点位置的设计和在整个工区进行空间随机炮点位置的设计。
2.1 理想情形下检波点间距满足完全高斯随机分布的随机观测系统设计
在完全随机观测系统中,要求采样点的空间位置分布符合高斯随机特征。即将检波点的空间位置作为一个二维随机变量ξ,以规则欠采样网格中采样点位置作为期望E{ξ},同时在Inline方向和Crossline方向上施加一个高斯随机扰动量Δξ。由高斯分布的性质可知,ξ的统计特征完全由其期望E{ξ}和标准差σ=(σx,σy)刻画。高斯随机观测系统参数也由期望与标准差刻画:
一是设定相对于理想密集采样网格的欠采样比例R,R为x、y方向欠采样比例rx与ry的乘积,即R=rxry。据此可计算规则欠采样的检波点网格,作为随机采样点的期望E{ξ}。
二是设定随机采样的标准差σx和σy,用以控制扰动程度。由高斯分布的性质可知,99.73%的随机变量分布在3个σ以内,因此可认为扰动量的最大值满足max{|Δξ|}=3σ。
表1中的数值实验显示了随机观测方法在单炮道集上的实施方式和数据恢复能力。
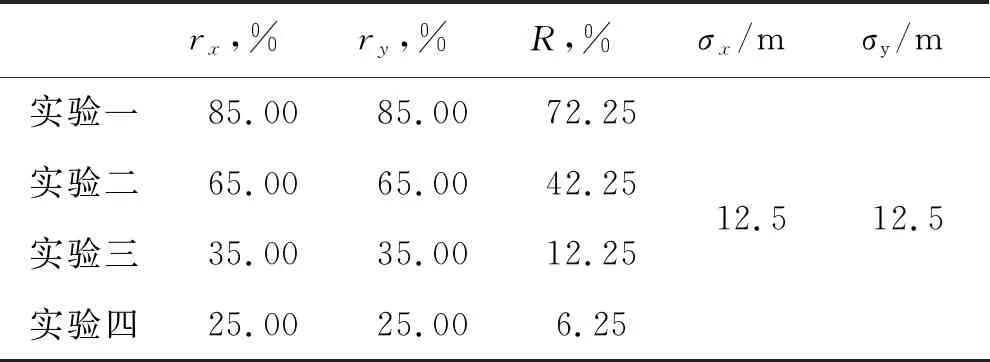
表1 单炮随机采集实验参数
单炮数据采集范围在Inline方向和Crossline方向均为625m,理想密网格间距dx=dy=12.5m。实验尝试了4组不同的欠采样比例。
图1展示了该组实验中采样比不同时检波点的分布情况。其中:图1a至图1d分别为在规则基础网格上抽稀到72.25%,42.25%,12.25%及6.25%的结果。图中黑点代表空间随机的检波点位置,右边矩形图代表沿Crossline方向检波点扰动量分布;下边矩形图代表沿Inline方向检波点扰动量分布。由图可见,检波点坐标在Inline和Crossline方向的统计特征符合离散高斯分布。在图1d中,相对于基础网格,由于只保留了6.25%的数据采样导致检波点数目过少,因此检波点坐标的统计特征与高斯分布存在一定偏差,进而会影响数据重建的质量。
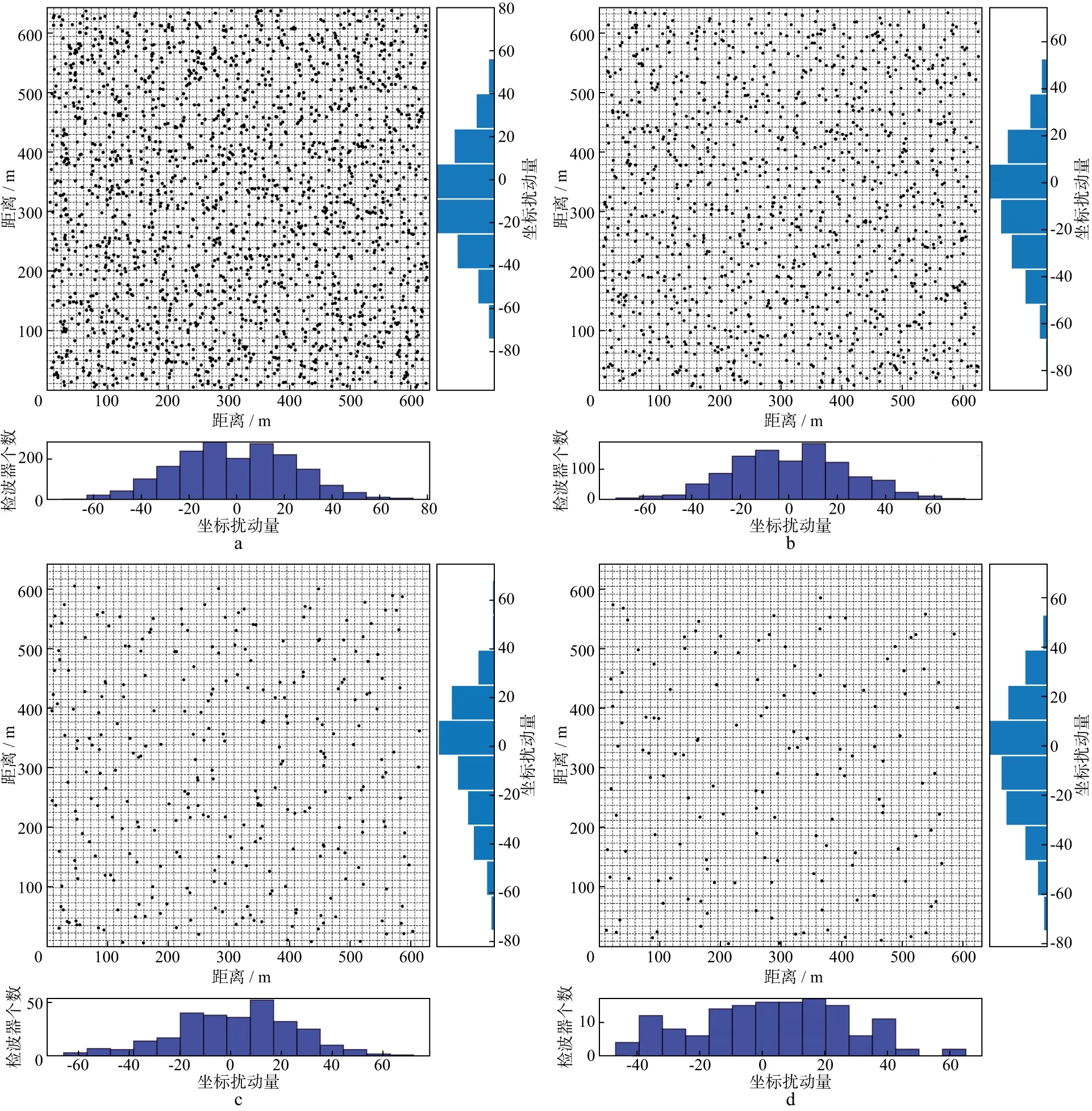
图1 完全随机观测系统中不同抽稀度情况下检波点的分布及其统计规律
随机观测数据的重建可表述为一个矩阵补全问题,并借助核范数优化算法求解[17]:
(2)
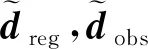
图2至图5分别展示了不同采样比例数据重建效果。由图可见,当采样比例逐步减小时,规则欠采样数据F-K谱呈现出愈发严重的假频,而CS观测数据F-K谱仅含有随机噪声,对数据的有效频谱影响有限。随机采集数据重建结果的品质,可由重建误差的能量衡量。当采样比例为72.25%、42.25%、12.25%和6.25%时,重建误差的能量比例依次为0.428%、0.623%、5.16%和22.2%,数据显示了欠采样比例与数据恢复品质呈正相关性,且当采样比例大于42.25%时,误差能量可低至1%以下,数据重建效果达到预期。事实上,从整个工区范围看,上述分析也适用于炮点随机布设的情形,尤其在当前强调正交与对称观测系统运用的情形下更是如此。
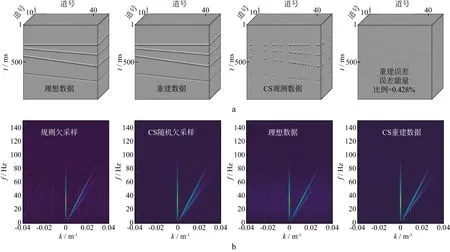
图2 采样比例为72.25%时数据重建结果(a)及对应的F-K谱(b)
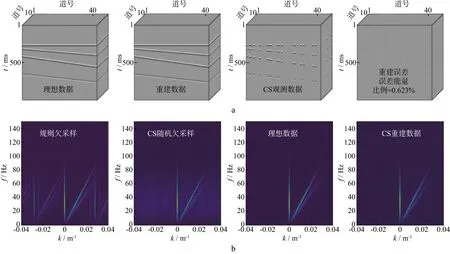
图3 采样比例为42.25%时数据重建结果(a)及对应的F-K谱(b)
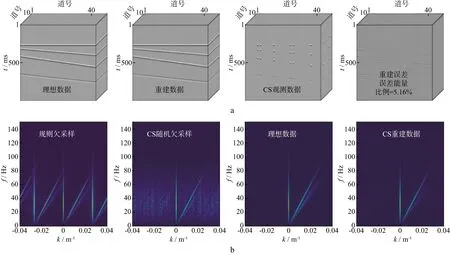
图4 采样比例为12.25%时数据重建结果(a)及对应的F-K谱(b)
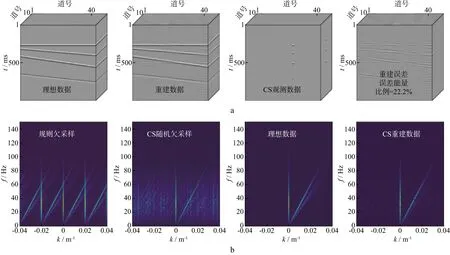
图5 采样比例为6.25%时数据重建结果(a)及对应的F-K谱(b)
2.2 考虑野外实际施工情况的随机观测系统设计
在设计实际观测系统时,首先要考虑单炮道集中检波点随机排放的方式,同时还要考虑到受高密度采集系统或常规观测系统基础网格的制约。因此,以常规单炮道集中检波点排列方式为基础,引入Inline和Crossline方向上的随机扰动。
图6为以常规单炮检波点排列方式为基础网格生成的检波点位置空间随机观测系统,考虑3种情形:①在常规单炮检波点排列基础上引入Inline和Crossline方向检波点位置的高斯随机扰动;②在常规单炮检波点排列基础上引入Inline方向检波点位置的高斯随机扰动,Crossline方向的线距高斯随机扰动;③在常规单炮检波点排列基础上仅引入Inline方向检波点位置的高斯随机扰动,Crossline方向的线间距保持等距。所有高斯随机扰动的方式按上述随机采样观测系统设计的原则执行。
从图6a中可以看出,空间随机放置的检波点间距在Inline和Crossline方向的统计特征符合离散高斯分布,高斯随机分布的检波点间距的均值等于常规网格上的检波点间距,这是我们提出的炮检点空间位置随机观测系统设计原则要求的,最有利于后续规则无假频数据的恢复。考虑到检波点同时在Inline和Crossline方向扰动在目前实际施工方案仍存在较大难度,进一步退化检波点空间随机的观测系统设计,仅考虑Inline方向上检波点采样间距的高斯随机扰动,而令线间距进行高斯随机扰动(图6b),由于线数太少(统计样本过少),统计直方图上已很难显示出线间距满足高斯分布的特点。另外,我们仅考虑Inline方向的检波点间距的高斯随机扰动,而线间距等于常规单炮数据采集时检波点排列的线间距(图6c)。
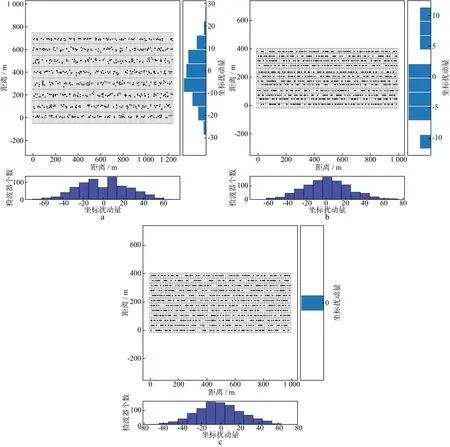
图6 以常规单炮检波点排列方式为基础网格生成的随机观测系统
以下为定量对比上述3种随机观测系统的数据重建质量,设计如下3个数值试验。
1) 以常规单炮检波点排列为基础网格,引入Inline和Crossline方向检波点位置的高斯随机扰动时随机观测系数数据重建结果的对比分析。
图7a所示兼容了当前测线滚动野外采集模式,采用此种观测模式虽然达不到全随机的采样效果,仍展现出较高的随机度,重建效果较好。在Inline方向25m网格,Crossline方向200m间隔的前提下,尝试引入随机扰动,成功重建12.5m网格的数据,误差能量的比例低至6.77%。
2) 以常规单炮检波点排列为基础网格引入Inline方向检波点位置的高斯随机扰动,Crossline方向的线距高斯随机扰动时随机观测系数数据重建结果的对比分析。
引入垂直测线方向的随机扰动,不便于提高布线效率,因此可退化为整条线采用统一的Crossline方向扰动量,即保持了一定的Crossline方向随机性,也简化了施工难度。在Inline方向25m网格、Crossline方向200m间隔的前提下,尝试采用此种观测方式,成功重建12.5m网格的数据,误差能量的比例低至8.77%(图7b)。
3) 以常规单炮检波点排列为基础网格,引入Inline方向检波点位置的高斯随机扰动,Crossline方向的线距保持等距时随机观测系数数据重建结果的对比分析。
整条线采用统一的Crossline方向扰动量,相对于均匀Crossline间距仍然有较高的施工成本。当放弃Crossline方向随机性时,仅保留Inline方向检波器随机扰动,数据重建质量是否满足要求。在Inline方向25m网格、Crossline方向200m间隔的前提下,尝试采用此种观测方式,成功重建12.5m网格的数据,误差能量的比例低至10.3%(图7c)。虽然误差能量有所上升,但有效信号仍然得到较好的恢复。
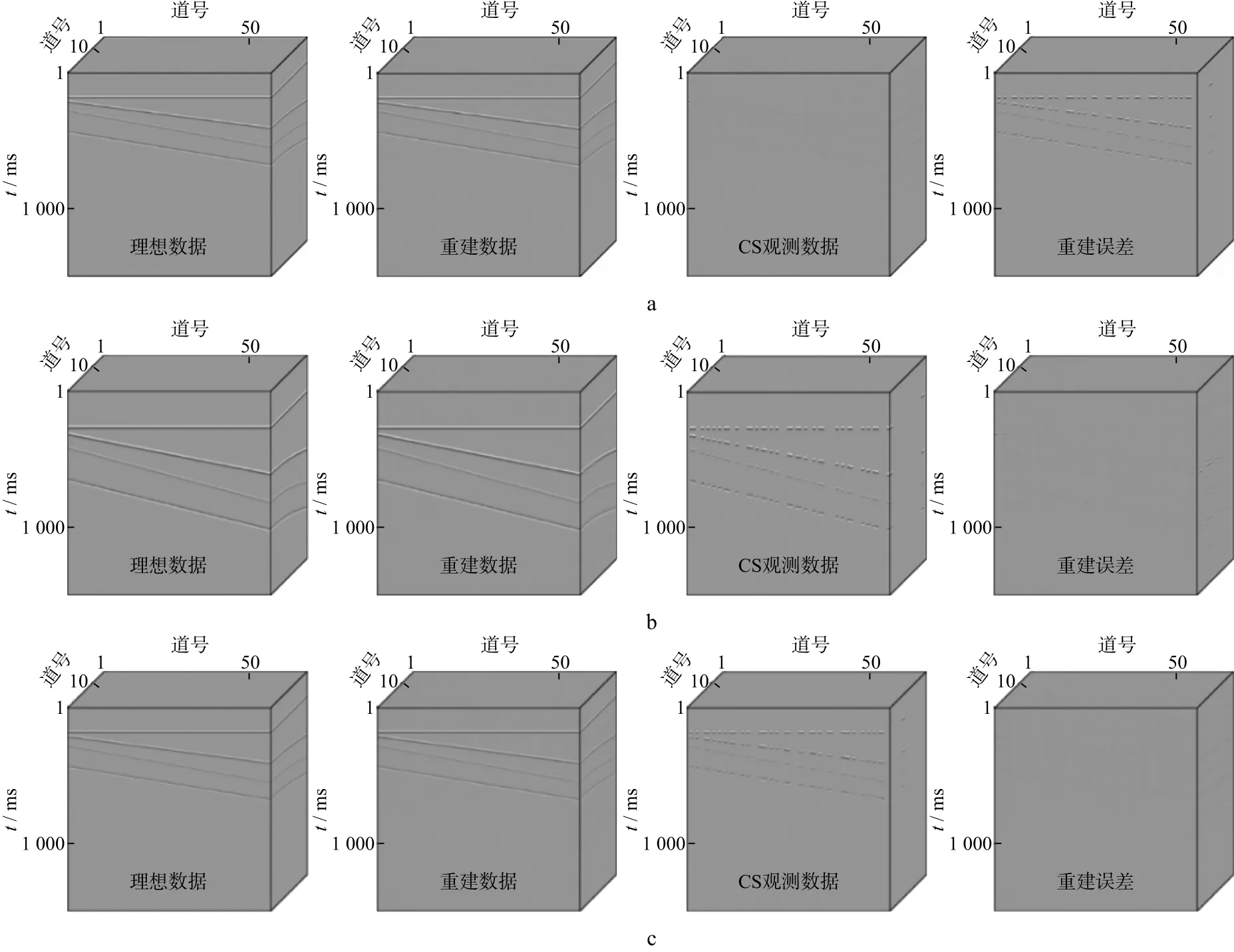
图7 数据重建结果对比
3 空间随机采样数据的规则无假频恢复测试
为了验证本文提出的随机观测系统设计思想与方法的有效性,利用胜利油田某工区典型的二维速度模型数据进行测试,该模型深度为4km,横向距离为12km(图8)。采用有限差分正演模拟方法,震源采用30Hz雷克子波,采样间隔为0.25ms,采样长度为4s。震源范围为1~11km,震源间隔为40m。检波点的覆盖范围为1~11km,检波点间隔为10m。
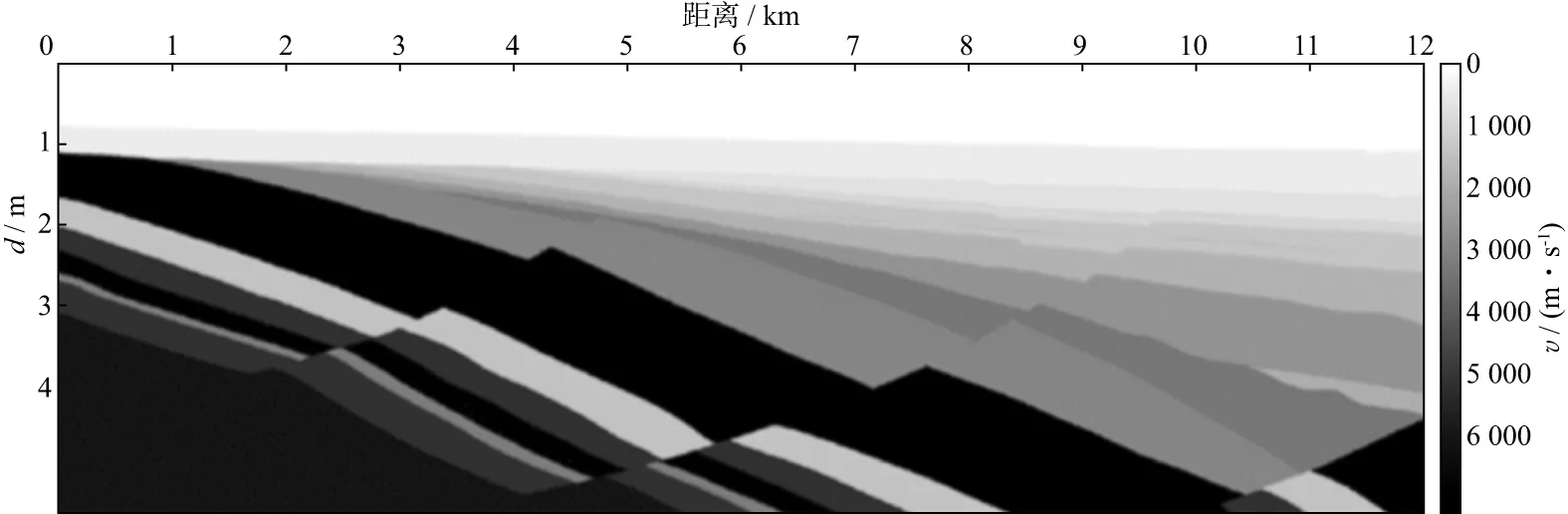
图8 胜利油田某工区二维速度模型
第1炮至第10炮的检波点位置如图9所示,图9a至图9d分别为检波点间隔(即道间距)分别为10m,20m,40m以及压缩感知采样(在10m规则网格基础上随机抽稀,仅保留12.5%的检波点)。即使仅采用12.5%的数据(高斯随机采样),经过压缩感知恢复,地震剖面中的有效信号也可以正确恢复(图10)。

图10 第120炮地震记录
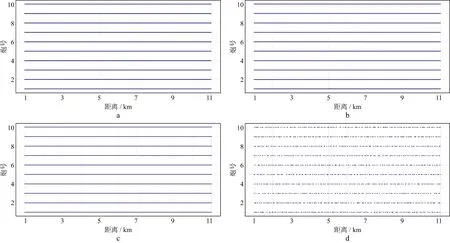
图9 第1炮至第10炮检波点覆盖位置
规则采样、随机采样及重建数据的F-K谱见图11。随机采样导致F-K谱的假频表现为随机噪声,与有效信号的频谱重叠在一起。经过压缩感知重构之后,有效信号频谱得到恢复。
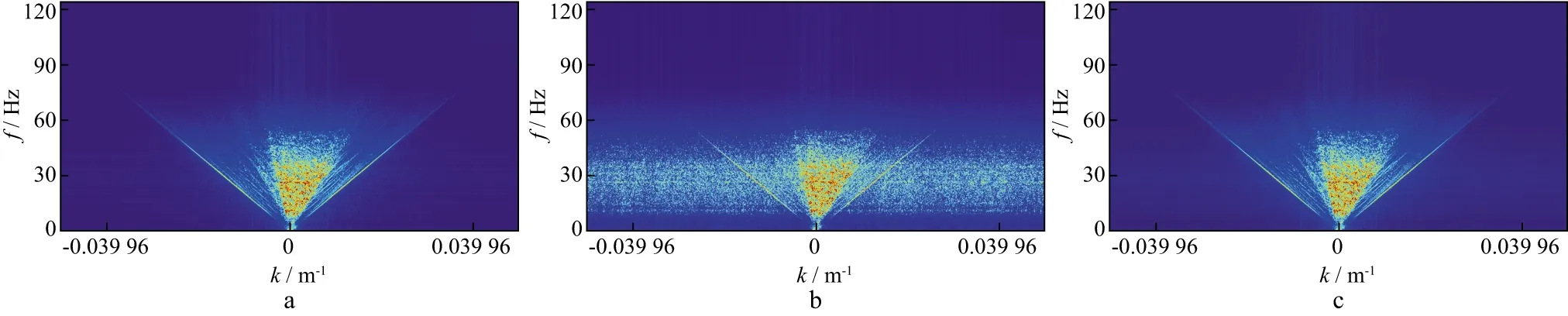
图11 不同采样间隔下的F-K谱
上述4种采样方式及重建数据的RTM成像结果(以第120炮为例)如图12至图16所示,图像经过Laplace滤波变换之后,随着规则采样间隔的增大,成像效果越来越差,偏移成像假象越来越多,当规则采样至40m时,成像剖面中出现较严重的假象,特别是浅层,效果更差。当采用12.5%的压缩比进行压缩感知采样时,可以看出,对应的成像结果由于压缩感知的随机采样,成像结果中出现较多的成像噪声。基于图15对应的数据,采用压缩感知重构之后的数据进行偏移,对应的成像结果中,成像噪声得到有效消除,成像结果和规则采样10m时的成像结果差别很小。因此在压缩感知采样理论指导下,可以采用较少的采样点数进行采样并有效恢复信号,得到较好的偏移成像结果。

图12 第120炮RTM成像结果(均匀采样10m间隔)

图13 第120炮RTM成像结果(均匀采样20m间隔)

图14 第120炮RTM成像结果(均匀采样40m间隔)

图15 第120炮RTM成像结果(压缩感知采样,10m规则网格抽稀12.5%)

图16 第120炮RTM成像结果(压缩感知恢复至10m规则采样结果)
所有炮的RTM成像结果如图17至图21所示,经过Laplace滤波变换之后,通过随机采样加压缩感知数据重建后,成像质量与10m规则采样数据的成像质量相当。

图17 所有炮RTM成像结果(均匀采样10m间隔)

图18 所有炮RTM成像结果(均匀采样20m间隔)

图19 所有炮RTM成像结果(均匀采样40m间隔)

图20 所有炮RTM成像结果(压缩感知采样,10m规则网格抽稀12.5%结果)

图21 所有炮RTM成像结果(压缩感知恢复至10m规则采样结果)
4 结论与讨论
基于实际应用可行性的考虑,本文提出了空间随机采样观测系统设计的基本原则,即在高密度地震数据采集(或常规地震数据采集)观测系统建立的基础网格基础上,按照高斯随机采样的理论要求,将规则欠采样的网格作为高斯随机采样位置的期望,分别在炮集范围进行空间随机检波点位置的设计和在整个工区进行空间随机炮点位置的设计。
考虑到实际应用的可行性,本文以特征波场(初至波场或标志性的反射波场)作为随机观测系统感知的对象,用频率域地震数据Hankel矩阵的低秩特性指导数据重建,通过生成符合高斯分布的随机观测系统,测试随机采样加压缩感知数据重建算法对于恢复无假频地震数据的能力及其影响因素。数值实验结果表明,通过随机采样加压缩感知数据重建后,基本能够恢复连续无假频的地震信号。同时,重建数据的偏移成像结果相对于随机采样甚至较大网格规则采样地震数据的成像质量,都有一定程度的提升,进一步验证了我们的判断。
在当前勘探目标和地表条件越来越复杂、低油价成为常态的情况下,空间随机采样能够以更少的炮检点获得同等投资情形下更高的质量成像结果。在“两宽一高”地震数据采集逐渐普及的情况下,对空间随机采样方法技术研究尤为重要,理论上,在压缩感知采样理论下开展“两宽一高”地震数据采集可以在控制投资成本的同时获得更高质量的成像结果。但在实际应用中,近地表散射和静校正量等因素导致地震信号的复杂度显著上升,因此对随机观测系统的设计及数据重建算法提出了更高的要求。对于复杂地震信号,如何将随机观测系统的设计与信号复杂度进行关联,需要开展进一步的研究。
致谢:感谢中国石油勘探开发研究院及西北分院、中国海油研究总院及湛江分公司、中国石化石油物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持!

