一种面向SoC的能量迹预处理方法*

蔡晓敏，李仁发，李少青，沈 高，邝世杰

(1.湖南大学信息科学与工程学院，湖南 长沙 410082;2.国防科技大学计算机学院，湖南 长沙 410073)

1 引言

密码设备运行时会不可避免地泄露一些物理信息，如功耗、电磁辐射、运行时间等旁路信息。侧信道攻击SCAs(Side Channel Attacks)正是利用物理信息与密钥的相关性，采集并统计分析物理信息以恢复密码设备的密钥。SCAs主要包括了功耗攻击[1]、电磁辐射攻击[2]和时间攻击[3]。 1996 年，Kocher[3]提出了一种基于运行时间攻击技术，成功破解了密钥。此后，非侵入式的SCAs技术在信息安全领域掀起了研究热潮[4-6]。1998年，Kocher等[1]提出了功耗分析PA(Power Analysis)攻击技术，该技术以其操作简易、适用范围广和成功率高等特点成为SCAs技术中最主要的攻击手段。如今，PA技术已经成功破解多种加密算法，如高级加密标准AES[7]、数据加密标准DES[8]、公钥密码算法RSA[9]以及智能卡[10]等。根据人们对密码设备的了解程度，PA技术分为简单功耗分析SPA[1]和差分功耗分析DPA[11]。

传统的DPA攻击[12]方法只利用加密算法的一位或多位中间值的功耗信息，其他部分的功耗数据被当作噪声不予考虑，导致功耗信息的利用率较低，所需功耗样本量较大。随着PA技术的不断优化，王小娟等[13]提出了一种基于类间距离的特征提取方法，提高了功耗信息的利用率。该方法的实现对象是微控制器，面对大规模的ASCI芯片或SoC芯片，攻击成功率将大幅度降低。刘政林等[14]提出了一种基于最大偏差的AES功耗分析攻击方法，计算出一组不同明文输入下的汉明重量和另一组不同明文输入下的汉明重量，选取2组不同明文输入下的汉明重量差为改进的功耗模型，但成功破解子密钥的功耗曲线仍需要5 120条，有效点个数为100。李金良等[15]通过差分峰值找到密钥的相关位置点，缩小攻击范围，只对部分功耗数据点进行分析，但攻击成功需要的功耗样本量较大，而且提取部分攻击点的方法缺乏理论支撑。

本文的贡献：面向SoC的DPA攻击过程，为解决功耗样本量大、提取点数较多的问题，提出了一种基于能量模型的能量迹分类方法，成功定位能量迹中的特征点。分别实测验证了基于汉明距离和汉明重量模型下得到的特征区间的攻击效果，大幅降低了DPA攻击的样本量和样本计算量。

2 研究背景

2.1 能量模型

目前，集成电路多数使用静态互补CMOS管实现，正常工作状态下，电路的功耗由静态功耗、动态功耗和短路功耗组成。动态功耗占总功耗的比例最大，用公式Pdyn=CLVDD2f0→1表示，其中，CL为负载电容，VDD为电源电压，f0→1为开关活动性。表1解析了各种输入状态下CMOS门电路的功耗情况。

Table 1 CMOS gate power consumption in different input states表1 不同输入状态下CMOS门功耗情况

由表1可看出，不同输入状态会产生不同的功耗，反之，不同的功耗必然意味不同输入状态，而差分功耗攻击正是利用功耗与内部数据的相关性来达到恢复密钥的目的的。

在DPA攻击中，通常必须将操作数映射为能量值，这是一种对设备的能量仿真。汉明距离模型[16]和汉明重量模型[17]2种能量模型在DPA攻击中很常见。

汉明重量模型的基本思想是假设能量消耗正比于所处理的操作数中值“1”的比特个数，而忽略在该数据之前和之后处理的数值。在攻击者对网表的内容一无所知，或者仅知道部分网表却不清楚该部分数据的前后处理情况下，通常采用汉明重量模型。

汉明距离模型的基本思想是计算数字电路在某个特定操作中0→1转换和1→0转换的总数量。值v0和值v1的汉明距离等于v0⊕v1的汉明重量HW(v0⊕v1)，也就是v0和v1中相异比特的个数。用式(1)来反映电路在该时段内的能量消耗情况:

E=aHW(v0⊕v1)+b

(1)

其中v0为某一寄存器的先前状态；v1为同一寄存器的后来状态；E为寄存器从v0状态切换到v1状态的能量消耗；a表示能耗比例系数；b表示与密钥不相关的能耗和噪声。

汉明重量模型原理简单、实现方便，在能量仿真中应用广泛。

2.2 基于均值差的DPA原理

基于均值差的DPA相关性检验方法操作简单，易于实现，其主要原理是攻击者选择密码算法过程中的某一位信号为目标信号(比如某个S-Box的输出结果)，按照目标信号在功耗点时刻H的取值“0”或“1”，对N次加密过程的功耗轨迹划分为2个类T1=(Ti[j]|H=1)和T0=(Ti[j]|H=0)，其中，1≤i≤N;每条功耗轨迹的长度是M，则j代表第i条轨迹的第j个采样点，1≤j≤M,Ti[j]为对应第j个采样点的电压采样。分别对T1和T0进行算术平均值运算后再相减得到差分功耗ΔH[j]，如式(2)所示:

ΔH[j]=∑Ti[j]∈T1Ti[j]/|T1|-

∑Ti[j]∈T0Ti[j]/|T0|

(2)

其中，|T0|和|T1|分别是T0和T1功耗轨迹数目，则|T0|+|T1|=N。当功耗轨迹条数N足够大时，除了目标信号，功耗轨迹中所有中间信号值均随机分布，则该部分功耗的均值差趋近0。若所得的差分功耗ΔH[j]曲线出现峰值，密钥猜测正确;反之，则密钥猜测错误。

3 基于能量模型的特征点定位方法

若一条能量迹的采样点数是15 000，条数为2 000，则攻击过程要计算一个2000×15000大小的矩阵，样本计算量极大，计算开销较大。由于噪声及外界干扰的引入，密码芯片运行时泄露的功耗并非全部都与密钥具有相关性。利用大量的采样点进行攻击时，可能将一些干扰项也包含在内，降低了攻击的成功率。若能定位到能量迹中与密钥具有较相关性的特征点，利用特征区间内的采样数据实施DPA攻击，将有效提高攻击效率。

由于噪声的存在，实际测量环境下采集到的能量迹存在着数据不对齐的问题，导致难以直接定位到中间值对应的能量迹位置。本文将与密钥具有最强相关性的采样点定为特征点。为了能够精准定位特征点，首先将测量到的能量迹进行分类处理，然后利用均值后做差的方法得到差分曲线，最后差分曲线的最大值即为特征点。利用能量模型定位特征点的方法需要提前掌握被攻击设备的正确密钥，因此该方法的适用范围是被攻击设备的设计者或者拥有被攻击设备的同款设备并可对其执行操作的人员。

下面给出定位特征点的具体步骤：

步骤1测量能量迹。测量密码设备在加密D组明文时的能量迹。将这D组明文记为PT= (PT1,PT2,…,PTi,…,PTD)，其中，PTi表示第i组明文，1≤i≤D。运行密码设备，测量到的多条能量迹记作T(i,j)= (Ti,1,…,Ti,j,…,Ti,N),其中，N表示能量迹的长度，1≤j≤N。全部的能量迹用矩阵T表示：

(3)

步骤2选取密码算法运行的中间值并映射为假设能量消耗矩阵。选取AES第1轮加密运算S盒的输出值作为中间值。正确密钥值假设为kcorrect计算出D组假设中间值。给定数据PTi和密钥假设kcorrect，对于所有D次加密行为，利用中间函数f计算出中间假设值vi=f(PTi,kcorrect)，得到中间数据矩阵V。利用汉明距离能量模型，将假设中间矩阵V映射为假设能量消耗矩阵HHD。利用汉明重量能量模型，将假设中间矩阵V映射为假设能量消耗矩阵HHW。

步骤3按照能量模型的取值对能量迹进行分类。HHD中的元素是能量迹的汉明距离值。HHW中的元素是能量迹的汉明重量值。以向量HHD为依据，将能量迹T(i,j)分为3类SHDt(1≤t≤3):

SHD1={T(i,j)|HD(T(i,j))∈{0,1,2}},

SHD2={T(i,j)|HD(T(i,j))∈{3,4,5}},

SHD3={T(i,j)|HD(T(i,j))∈{6,7,8}}

(4)

若能量迹T(i,j)的汉明距离为0,1,2，则归于SHD1类；若能量迹T(i,j)的汉明距离为3,4,5，则归于SHD2类；若能量迹T(i,j)的汉明距离为6,7,8，则归于SHD3类(针对的是2组8 bit数据)。同样，以向量HHW为依据，将能量迹T(i,j)分为3类SHWt:

SHW1={T(i,j)|HW(T(i,j))∈{0,1,2}},

SHW2={T(i,j)|HW(T(i,j))∈{3,4,5}},

SHW3={T(i,j)|HW(T(i,j))∈{6,7,8}}

(5)

步骤4分别对类SHDt和类SHWt进行均值处理，得到3条正确密钥下的均值能量迹RHDt和RHWt。

(6)

其中，每一个|SHDt|为对应类SHDt中能量迹的数量，每一个|SHWt|为对应类SHWt中能量迹的数量。

步骤5选取一个错误的密钥假设kwrong，重复步骤2～步骤4得到kwrong下的3条均值能量迹WHDt和WHWt。RHDt和WHDt相减，得到3条差分迹ΔDHDt。同样，将RHWt和WHWt相减，得到汉明重量模型下的3条差分迹ΔDHWt。3条ΔDHDt同时出现最大尖峰处的采样点便是汉明距离模型下得到的特征点PHD。3条ΔDHWt同时出现最大尖峰处的采样点便是汉明重量模型下得到的特征点PHW。图1和图2表示在2种能量模型下得到的ΔDHDt和ΔDHWt曲线。图1和图2中的正确密钥kcorrect是197，错误密钥kwrong是18。汉明距离模型下得到的特征点PHD是6 113，汉明重量模型下得到的特征点PHW是5 616。其中，均值能量迹WHDt和WHWt的求解公式如式(7)所示：

(7)

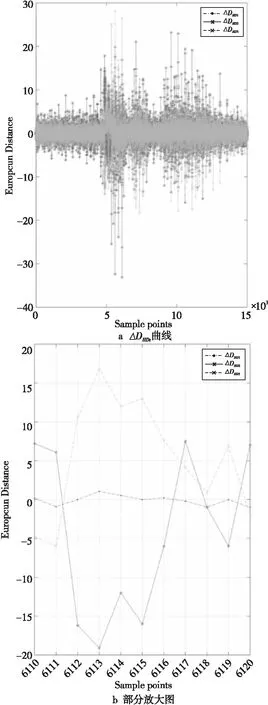
Figure 1 Curves ΔDHDt and partial enlargement of hamming distance energy model图1 汉明距离能量模型下的ΔDHDt曲线及部分放大图

Figure 2 Curves ΔDHWt and partial enlargement of hamming weight energy model图2 汉明重量能量模型下的ΔDHWt曲线及部分放大图

4 实测验证

首先搭建一个实际能量采集平台用于测量SoC芯片的能量迹，然后利用能量模型定位方法，确定出2种能量模型下的2个特征点，最后截取特征点附近适量的采样点构成特征区间并开始实施DPA 攻击。为了将计算成本由2128降为16×28，DPA攻击的核心思想是分而治之，实施过程也是8位一组。本文涉及到的密钥也是指128位AES算法的8位子密钥。采用文献[18]的欧氏距离波动系数α评估攻击结果，0<α<1。α越接近于1，表示结果密钥对应的尖峰具有越高的独立性，结果密钥的可靠性越高。

Figure 3 Energy acquisition platform图3 能量采集平台

实现对象为国内某款SoC芯片，设为专用的密码协处理器。协处理器与其他部件处于同一PCB板上，传导噪声较大，增强了准确定位特征点的难度。图3是搭建的功耗采集平台，主要包括SoC芯片、工控机箱、采集卡和PC机等。SoC芯片通过2条高速数据线与采集卡连接。采集卡采集SoC芯片内核路径上的0.1 Ω采样电阻2端的电压变化并传送给上位机软件。采集卡的采样频率为5 GS/s，采样深度为2 Gpts，采集精度为10 bit。为了验证特征点的有效性，本文随机选择10个不同的正确密钥。针对每个密钥随机选择输入2 000个随机明文，利用能量采集平台采集到 2 000条能量迹，总共采集20 000条能量迹。

利用第3节的定位方法，得到汉明距离能量模型下的特征点是6 113，汉明重量模型下的特征点是5 616。分别截取特征点附近2,5,10,15,20,50,100,200,400个采样点构成特征区间，作为DPA攻击的输入数据实施攻击，并记录攻击结果的α值，结果如图4和图5所示。

Figure 4 Attack results of different characteristic intervals under hamming distance energy model图4 汉明距离能量模型下的不同特征区间的攻击结果

Figure 5 Attack results of different characteristic intervals under hamming weight energy model图5 汉明重量能量模型下的不同特征区间的攻击结果

Figure 6 Sample size under different attack methods图6 不同攻击方法的样本量统计

从图4中可看出，汉明距离能量模型下的特征区间长度为5时，α的中位数最大。从图5中可看出，汉明重量能量模型下的特征区间长度为20时，α达到最大。因此，在最佳特征区间的长度上，汉明距离能量模型得到的特征点具有较低的计算开销。

作为对比，最佳特征区间与文献[19]的ICA(Independent Component Analysis)方法和无预处理的传统DPA方法比较，结果如图6所示。从图6可以看出，本文的特征区间方法在样本量为178时，攻击成功率达100%，而文献[19]的ICA方法需要样本量为600才能达到100%，传统DPA在样本量为600时的攻击成功率为86%。因此，利用汉明距离能量模型得到最佳特征区间所需要的能量迹条数较少，降低了计算开销。

本文特征区间的结果参数与其他文献相对比的结果如表2所示，其中“-”代表该文献中未涉及到该参数.本文芯片的每个周期采样点为250。一次完整的加密运算占用30个时钟周期，7 500个采样点。由表2可知，与文献[14,15]相比，利用特征区间的方法降低DPA攻击样本计算量的效果显著，本文方法节约比例最大，只占其他文献的1/2左右；与文献[14,19]相比，缩减了大量的样本量。

Table 2 Comparison of parameters of different methods表2 不同方法的参数比较

5 结束语

面向SoC对象，为解决DPA攻击样本计算量和样本量较大的问题，本文提出一种基于能量模型的特征点定位方法。从实验结果看出，基于汉明距离能量模型得到的特征区间取得了良好的效果，极大地压缩了破解密钥的样本计算量，降低了计算开销。在未来的研究中，计划进一步拓展特征点定位方法的适用范围以及攻击场景。