稳定物质转移通道形成双黑洞

李槛杉

(1. 中国科学院 云南天文台，昆明650011； 2. 中国科学院大学，北京100049)

1 引 言

大质量恒星在宇宙中占有重要地位。这些恒星演化到中心核燃料耗尽时，通常会发生超新星爆炸现象，向星际空间抛射大量重元素[1]，对星系的化学演化有巨大影响[2]。大质量恒星的恒星星风、超新星爆炸等过程能搅动星际气体，进而可能会影响新一代恒星的形成[3]。大质量恒星演化的产物是致密星，包括中子星和恒星级黑洞。宇宙中一些重要天文现象与致密星密切相关，包括X 射线双星、伽马暴以及双致密星并合产生的引力波事件等。

理论研究方面，1999 年Fryer[4]估算出能形成黑洞的恒星质量范围。如果不考虑星风物质损失，初始质量为(25 ～40)M⊙的恒星一般会经历超新星爆炸，然后通过吸积回落物质形成黑洞；初始质量大于40 M⊙的恒星一般会直接坍缩为黑洞，不经历超新星爆炸[4]。该数值具有一定的不确定性，只是一个典型的值。如果考虑星风损失，演化过程就更加复杂，而且存在较大不确定性。Belczynski 等人研究了大质量单星演化初始质量与形成黑洞质量的关系，在太阳金属丰度情况下，可以形成的最大黑洞质量大约为15 M⊙，而在金属丰度较低(Z =0.000 1)的情况下可以形成的最大黑洞质量为94 M⊙[5]。

观测研究方面，根据恒星初始质量函数，大质量恒星在所有恒星中占比小，并且演化时标较短。除去已经探测到的引力波事件，观测研究中能准确测量质量参数的中子星系统有60 多个[6,7]，而观测到X 射线双星系统中的黑洞有20 多个[8]，只有大约10 个系统能准确测量黑洞动力学质量，大多数黑洞质量范围在(5 ～10)M⊙之间。银河系中已发现的X射线双星系统中，最大黑洞质量约为15 M⊙，近邻星系中存在质量更大的黑洞：M33 X-7(MBH= 15.65 M⊙±1.45 M⊙)[9], IC 10 X-1 (MBH≈23 M⊙～24 M⊙)[10,11], NGC 300 X-1(MBH＞10 M⊙)[12,13]。研究发现这3 个大质量黑洞所处的区域金属丰度都较低：星系IC 10中X-1 的金属丰度Z ≈0.004[14]，星系M33 中X-7 的金属丰度Z ≈0.008，星系NGC 300中X-1 的金属丰度Z ≈0.006[15]。

Sana 等人研究发现，大质量恒星大多以双星的形式存在，大部分系统演化过程中会发生双星相互作用[16]。最终可以形成双致密星，包括双中子星(NS-NS)、中子星-黑洞系统(NS-BH)和双黑洞(BH-BH)。这些前身星系统一般会经历一两次超新星爆炸和几个阶段物质转移，以及一次或者两次公共包层演化阶段[5,17-20]。双中子星系统的研究可以参见文献[21]，大质量双星在超新星爆发前的演化研究可以参见文献[22—24]。

现阶段大质量恒星的演化仍然存在较多不确定的问题[25]，如星风物质损失率、超新星爆炸机制和反冲速度等。而双星的相互作用使得大质量双星系统演化更加复杂[24]，包括物质转移和公共包层演化[26]等问题。

1984 年Bond 等人提出双黑洞并合可以作为潜在的引力波源[27]，而对它的研究始于20世纪90 年代[28]。一些研究者提出银河系高金属丰度环境下的恒星是形成双黑洞的潜在候选体[17,29]，后来Belczynski 等人[30]研究表明高金属丰度环境将抑制双黑洞的形成，提出低金属丰度的恒星才是形成大质量黑洞的主要候选体[31]。此外，星族III 恒星也被考虑作为形成双黑洞及引力波源的前身星系统[32]。

20 世纪初爱因斯坦预言了引力波，但是引力波产生的形变效果微弱，探测存在很多问题。1975 年，Hulse 和Taylor[33]发现了脉冲双星PSR B1913+16，1982 年Weisberg 和Taylor[34]观测研究发现这个双星系统正在损失能量，间接证实了引力波的存在。20 世纪90年代初，美国科学家开始建造激光干涉引力波天文台(Laser Interferometer Gravitationalwave Observatory，以下简称LIGO)，LIGO 在1999 年建成，经过10 多年的改进、升级，2016 年2 月LIGO 发布了探测到的第一个引力波信号GW150914[35]。GW150914 来自两颗大质量黑洞并合，[36,37]。LIGO 为研究大质量恒星演化及恒星级黑洞提供了新的观测手段，第一次证实了恒星级大质量双黑洞的存在[38]。随后，LIGO 和Virgo陆续探测到更多的双黑洞并合产生的引力波信号，以及双中子星并合产生的引力波信号[39]。到目前为止，LIGO 和Virgo 总共已经探测到了10 个双黑洞并合的引力波事件和1 个双中子星并合的引力波事件，表1 列出了对应引力波事件的相关参数。

LIGO 现阶段探测到的引力波信号中大部分黑洞质量较大，例如LIGO 探测到的第一个引力波信号GW150914 是来自(35.6+30.6)M⊙的大质量双黑洞并合成为一个约63M⊙的大质量黑洞[40]，Belczynski 等人的研究表明通过公共包层演化通道可以形成这样的双黑洞[5]。目前的模型中能形成双黑洞并合的通道主要有三种：(1)孤立的双星演化通道[5,41,42]；(2)化学均匀演化通道[43-45]；(3)动力学演化通道[46-48]。对形成类似GW150914 事件中的大质量双黑洞，三种通道都有一个共同特点，要求恒星是在低金属丰度的环境下形成，避免剧烈的星风物质损失。如果金属丰度较高，星风物质损失率大，最后留下的质量会低于30M⊙[49, 50]。

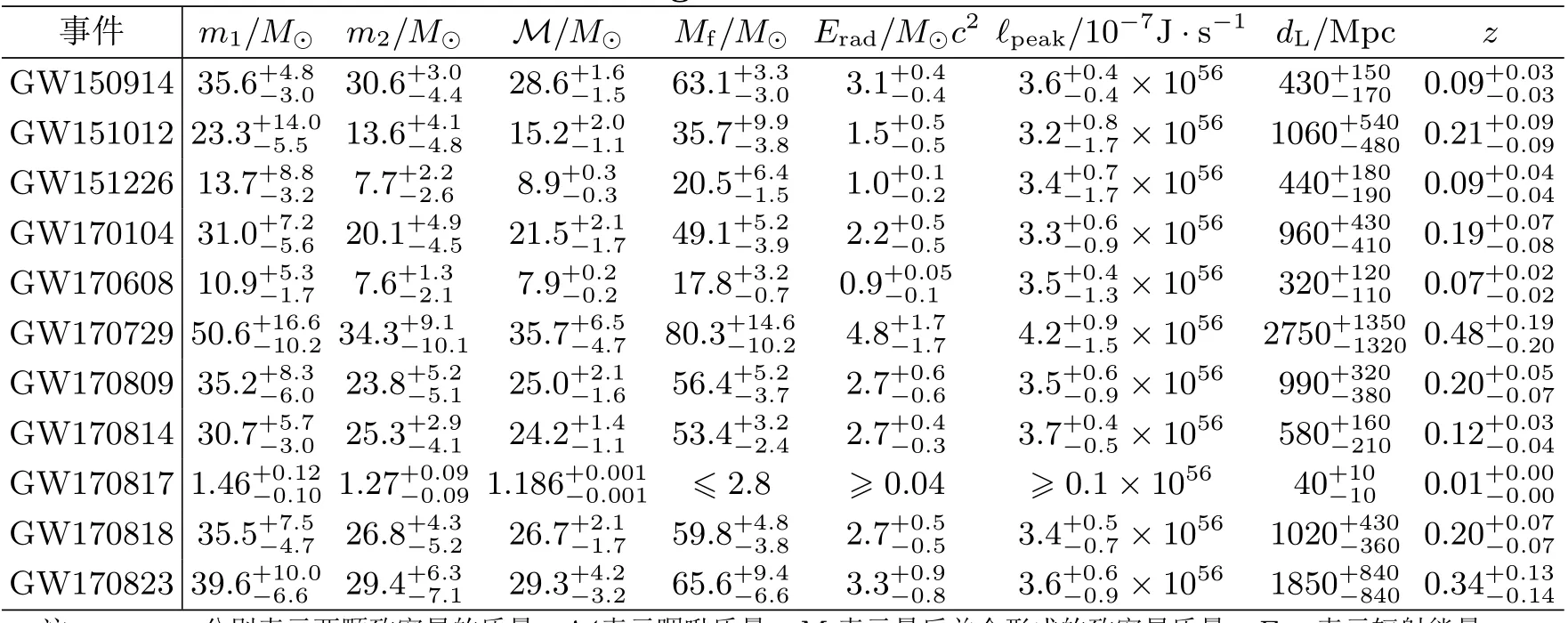
表1 LIGO 和Virgo 探测到的引力波事件相关参数[40]

本文采用恒星演化程序MESA[51-53]研究孤立大质量双星系统通过稳定物质转移通道(不包含公共包层演化阶段)，最终形成恒星级大质量双黑洞，研究结果能解释部分引力波事件。第2 章介绍了我们工作中相关过程的计算方法以及初始输入参数；第3 章介绍研究结果，包括最终形成的双黑洞的质量分布以及并合时标等；第4 章是总结和展望。

2 模型与计算方法

我们采用恒星演化程序MESA 详细研究大质量双星系统的演化，输入初始参量，包括恒星质量、金属丰度和轨道周期等。恒星演化到中心He 燃烧结束时，停止演化，然后提取恒星质量以及CO 核质量等参量，依据超新星爆炸机制计算形成黑洞的质量。

2.1 相关物理参数

我们在处理对流过程中采用标准混合长模型[54]，混合长参数α= 1.5。采用勒都判据，半对流过程依据Langer 等人[55]的研究，有效参数取αsc=1.0，采用MESA 程序提供基本核反应元素网格“basic.net”。处理对流超射依据Brott 等人[56]的研究，对流超射参数取0.335倍的压强标高，恒星对流核的半径为勒都判据计算的半径加上0.335Hp，Hp表示对流核边界处的压强标高。通常对流超射会形成质量较大的恒星核，尤其是主序燃烧阶段，对流超射会导致形成的He 核质量较大。

金属丰度对恒星的演化有重要的影响[24]，在不同星系中以及同一个星系中不同时间形成的恒星金属丰度不同。Belczynski 等人[5]的研究表明，只有在低金属丰度环境(Z ＜10%Z⊙) 下才能形成大质量双黑洞(MBH＞30 M⊙)。我们的工作建立在他们的研究基础上，最低金属丰度取Z = 0.000 1 (Z = 0.5% Z⊙)，最高金属丰度取Z = 0.002(Z =10%Z⊙)，Z 定义为比He 重的所有元素所占的质量分数，在最低和最高金属丰度之间选取5 个值，分别是：0.000 1,0.000 2,0.000 5,0.001,0.002。初始He 元素丰度依据Brott 等人[56]的研究，当Z =0 时，Y =0.2477[57](Y 表示He 元素丰度)，Z =Z⊙时，Y =0.28[58]，He 元素丰度与金属丰度呈线性变化关系。

我们只研究形成黑洞的情况，不考虑形成中子星的情况，用MESA 模拟恒星演化得到，恒星初始质量为20 M⊙时，演化到中心He 燃烧结束，形成的CO 核质量约为6 M⊙。依据Fryer 等人[59]的快速超新星爆炸机制，CO 核质量为6 M⊙是形成中子星和黑洞的分界点。恒星初始质量越大，在演化程序计算过程中越容易出现计算不收敛的问题，经过我们的测试，初始质量为80 M⊙的恒星在程序计算演化过程中收敛情况较好；所以在我们的研究中，主星(双星系统中初始质量较大的恒星)的初始质量MPZAMS取(20 ～80)M⊙。有研究表明双星在主序阶段发生相互作用，初始质量比大于0.65 时物质转移是动力学稳定的[60,61]；如果初始质量比小于0.65，伴星吸积物质会快速膨胀，最终导致双星并合[62]。我们在研究中不考虑并合情况，所以初始双星质量比取q1=0.7, 0.8, 0.9，其中q1=MSZAMS/MPZAMS，次星(双星系统中初始质量较小的恒星)的初始质量MSZAMS依据q1和主星质量取值。

双星初始轨道周期依据Kruckow 等人[63]的研究，对于OB 型恒星，为了避免Darwin 不稳定性，我们选取最小初始轨道周期为3 d，最大周期为100 d。

通常情况下恒星存在自转速度，在双星系统中某些情况下次星吸积物质可能达到很高的自转速度[64]，会改变恒星的演化轨迹及演化结局。一般情况下，恒星自转速度较慢，远小于破裂速度时，自转对恒星演化的影响很小[56]，我们在研究中没有考虑恒星自转的影响。

2.2 星风模型

相对于小质量和中等质量(MZAMS≤8 M⊙)的恒星，大质量恒星(MZAMS≿10 M⊙)演化过程中星风物质损失显得尤为重要。大质量恒星外层辐射的光子动量很大，星风物质损失率也很大。初始质量MZAMS＞20 M⊙的恒星，甚至在主序阶段，快速星风物质损失会影响其后续演化。而后主序演化阶段，星风物质损失变得更为关键，它可以影响恒星的亮度、燃烧寿命、有效温度，He核质量以及恒星最终的命运[65]。

Vink 等人[66]的研究表明，星风物质损失率在温度为1.25×104K 和2.5×104K 时存在跳变。我们的工作以Brott 等人[56]的星风模型为基础，在有效温度较高时(Teff＞25 000 K)，采用Vink 等人[66,67]的星风物质损失模型；在有效温度较低时(Teff＜25 000 K)，比较Vink等人[66,67]的星风模型与Nieuwenhuijzen 和de Jager[68]的经验星风模型的物质损失率，选择两者中物质损失率较大者。我们在Yoon 等人[69]研究的基础上，考虑恒星表面元素对星风物质损失率的影响，并对含有富H 包层的恒星(Ys＜0.4，Ys表示表面He 丰度)，采用Vink等人[66,67]的星风模型计算质量损失率；对于不含H 包层的贫H 恒星(Ys＞0.7)，采用1/10的Hamann 等人[70]沃尔夫-拉叶星的星风物质损失模型计算质量损失率；对于0.4 ＜Ys＜0.7的情况，在两种星风模型之间线性插值。

我们采用Vink 等人的星风损失率公式[66]计算质量损失率。有效温度处在27 500 ＜Teff≤50 000 K 时，质量损失率表示为：

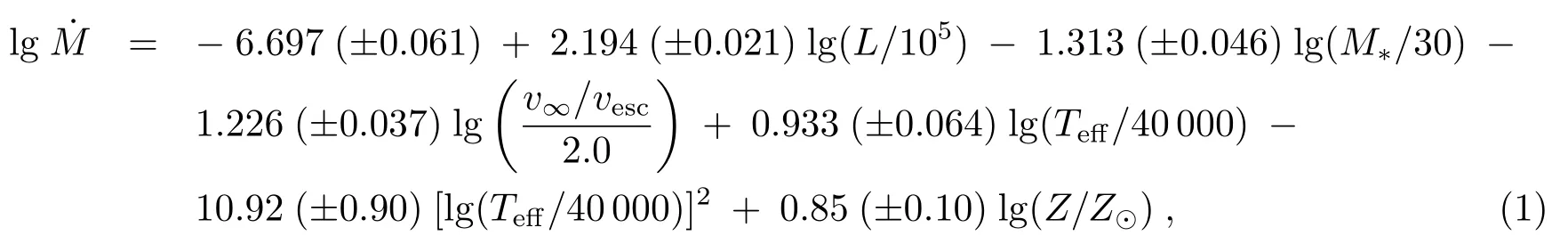
其中，v∞/vesc=2.6。

有效温度为12 500 ～22 500 K 时，质量损失率表示为：

其中，v∞/vesc=1.3。

当有效温度Teff在22 500 ～27 500 K 范围内时，跳变温度为：

其中，

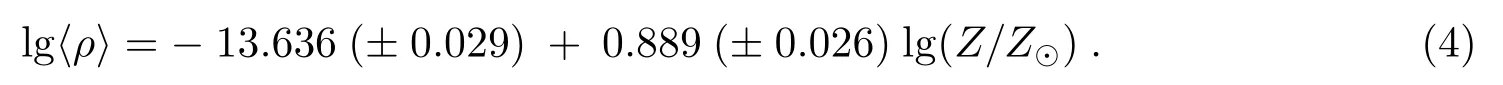
Nieuwenhuijzen 和de Jager 的星风损失率[68]表示为：

Hamann 等人的星风损失速率[70]表示为：

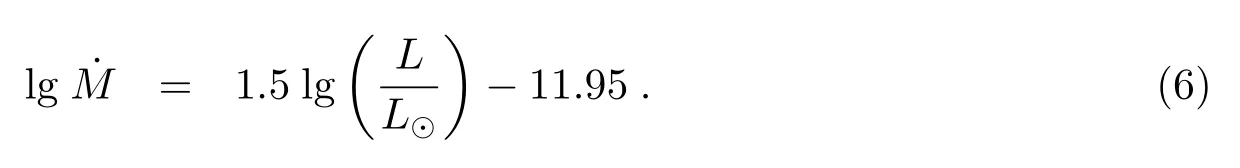
2.3 反冲速度

大质量恒星演化会通过超新星爆炸形成中子星或黑洞，如果初始质量较大，则可能会直接坍缩形成黑洞(依据CO 核质量，在6 M⊙≤MCO＜7 M⊙和11 M⊙≤MCO情况下判定恒星直接坍缩形成黑洞，参见2.7 节)。超新星爆炸会抛射物质，而爆炸过程通常是各向异性，爆炸会导致新形成的致密星有反冲速度[71]。Hobbs 等人[72]研究分析了233 个脉冲星的速度分布，依据样本的一维和二维速度分布导出了脉冲星诞生时的三维速度分布，可以用σ = 265 km·s-1的一维麦克斯韦速度分布拟合脉冲星的三维速度分布。依据Fryer 等人[59]的研究，如果超新星爆炸后有回落物质，则反冲速度需要乘相应的因子：Vkick=(1-ffb)Wkick，其中ffb表示物质回落系数，Wkick表示Hobbs 等人[72]研究给出的反冲速度；对直接坍缩形成黑洞的情况(ffb=1)，则表示黑洞诞生时反冲速度为零。

由于黑洞的观测样本较少，黑洞的反冲速度不确定性较大。一些研究者研究了X 射线双星系统中黑洞的反冲速度，1995 年Brandt 等人[73]研究表明，黑洞诞生时具有反冲速度更容易解释GRO J1655-40 的空间速度；2005 年Willems 等人[74]给出GRO J1655-40 的反冲速度上限约为210 km·s-1。2001 年Mirabel 等人[75]研究表明XTE J1118+480 的空间速度较大，Gualandris 等人[76]认为这个系统中的黑洞诞生时具有反冲速度，2007 年Fragos 等人[77]研究给出XTE J1118+480 的反冲速度约为200 km·s-1。2012 年Wong 等人[78]研究发现Cygnus X-1 的反冲速度相对较小，约为几十千米每秒，最大不超过77 km·s-1。2009 年Miller-Jones 等人[79]研究得到黑洞X 射线系统V404Cyg 的本动速度约为40 km·s-1，表明黑洞形成时的反冲速度不大于40 km·s-1。研究表明对某些黑洞候选体，如GRS 1915+105和Cygnus X-1，似乎不需要反冲速度就能解释它们的空间速度[80,81]。

2.4 计算轨道间距

在形成致密星的过程中系统有物质损失，会改变双星系统的轨道间距，本文依据Tauris等人[82]的研究，对通过超新星爆炸，吸积回落物质形成黑洞的情况(有反冲速度)，采用式(7)计算超新星爆炸后的轨道间距变化：

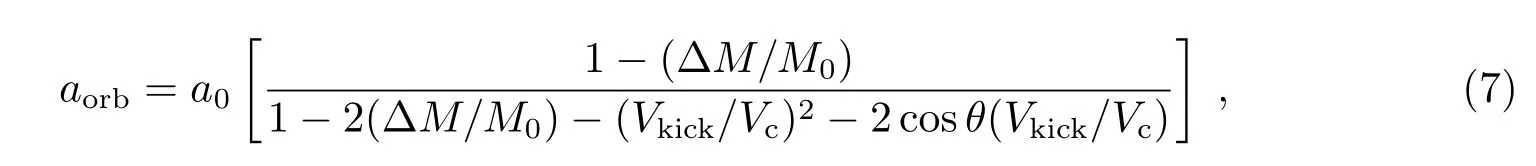
其中，aorb表示超新星爆炸后的双星系统轨道间距，a0表示超新星爆炸前的双星系统轨道间距，ΔM 表示超新星爆炸损失的质量，M0表示超新星爆炸前双星系统总质量，Vkick表示新诞生黑洞的反冲速度，Vc表示黑洞前身星轨道速度，θ 表示反冲速度和轨道速度的夹角，方向随机。对应的系统轨道椭率e 计算如下：

其中，系统轨道能量Eorb=-GMBHM2/2aorb，轨道角动量为：μ 表示坍缩形成黑洞后系统的约化质量，φ 表示反冲速度在超新星前身星轨道速度垂面上的投影与系统轨道平面的夹角。在椭圆轨道情况下，随着恒星演化，其轨道会圆化，由于轨道角动量守恒，圆化后的轨道间距为acirc=(1-e2)aorb。

对恒星直接坍缩形成黑洞的的情况(反冲速度为零)，圆化后的轨道间距表示如下[82]：

其中，mtot表示坍缩形成黑洞后双星系统的总质量，M1, M2分别表示两颗子星质量，MBH表示黑洞的质量。

2.5 轨道角动量

MESA 程序[53]中轨道角动量计算公式为：，其中，表示轨道角动量变化率，表示引力波辐射引起的角动量损失率， ˙Jml表示物质损失带走的角动量，表示自转较快的小质量恒星中磁滞对角动量损失的影响， ˙Jls表示恒星自转和轨道耦合导致的角动量损失。我们在研究中只考虑物质损失对轨道角动量的影响，考虑物质从吸积星损失，同时物质损失带走吸积星的角动量，具体计算公式如下[83]：

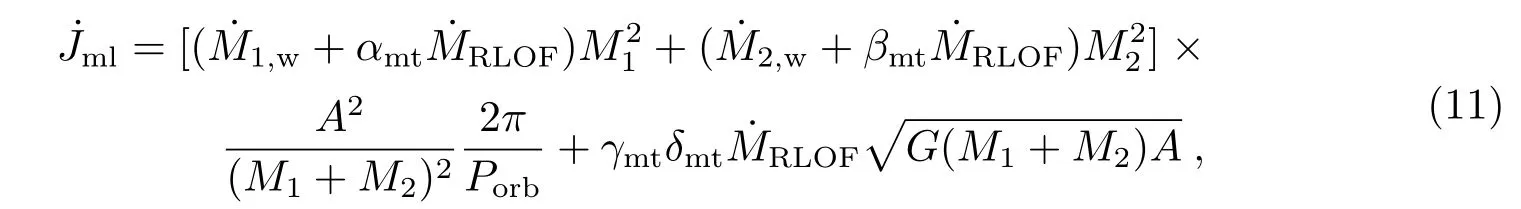
2.6 物质转移

双星演化中，当供给星充满洛希瓣时，双星发生物质转移，供给星通过拉格朗日点向伴星转移物质。物质转移分为稳定物质转移和非稳定物质转移两种情况，我们采用质量比q2(在物质转移开始时的双星质量比)来判定物质转移是否稳定，在这里质量比定义为q2=Mdon/Macc，其中，Mdon为供给星质量，Macc为吸积星质量。通常依据供给星演化阶段(主序阶段、赫氏空隙阶段和巨星支阶段)不同，发生物质转移对应临界质量比的取值不同，我们主要考虑在主序阶段和赫氏空隙早期阶段发生稳定物质转移，统一取qlimit= 2.5，较小的临界质量比更严格地限制了发生稳定物质转移情况的参数空间[63]。对于q2＜qlimit的情况，系统物质转移是动力学稳定；对于q2＞qlimit的情况，系统物质转移是动力学非稳定的，最后形成公共包层。

我们在研究物质转移方式时采用MESA 程序中提供的洛希瓣模型[53]，模型要求供给星严格保持在洛希瓣内，超出洛希瓣的物质通过内拉格朗日点转移到吸积星。我们在计算中，取伴星吸积率fmt=0.5[84](其中αmt=0, βmt=0.5, γmt=0)。星风物质吸积率采用Hurley等人[85]的星风吸积过程，即Bondy-Hoyle 机制。

伴星吸积物质考虑了爱丁顿吸积率[86]限制：吸积星为非致密星情况下，爱丁顿吸积率较大，吸积率不受爱丁顿吸积率的限制；吸积星为致密星时，吸积率会受爱丁顿吸积率的限制。如果黑洞的吸积率大于爱丁顿吸积率黑洞的吸积光度会超过爱丁顿光度极限，此时辐射压会将多余的物质推离系统，黑洞将以爱丁顿吸积率吸积物质。因为爱丁顿吸积率的限制，在物质转移过程中黑洞只能吸积非常少的物质。

2.7 黑洞质量的计算

目前很多研究者提出多种模型研究超新星爆炸机制，不同的模型结果存在差异，具体可以参见Spera 等人[50]的研究。我们的研究中采用Fryer 等人的快速超新星爆炸机制[59]，在这种模型中统一设Mproto=1.0 M⊙，具体计算公式如下：

其中，ffb表示超新星爆炸时抛射的物质中回落到原致密星(proto-compact object)上的比例系数(0 ～1)，0 表示没有回落物质，1 表示抛射物质全部回落。M 代表超新星爆炸前的恒星质量，Mproto表示原致密星的质量，MCO表示CO 核的质量。a1=(0.25-1.275)/(M -Mproto), b1=1-11a1。

Mfb表示爆炸后回落到原致密星上的物质质量，Mrem,bar表示剩余重子物质的质量。Mrem表示最终形成致密星的引力质量。对形成中子星的情况采用Timmes 等人[87]的公式：

计算最终形成中子星的质量。

对形成黑洞的情况，依据Fryer 等人[59]的研究，采用公式如下：

计算最终形成黑洞的质量。

观测研究中最大的中子星质量约为2 M⊙[88]，统计分析测量黑洞的质量分布表明黑洞的质量不会低于4.5 M⊙[8,89,90]。这导致中间有一段质量分布间隙(2 M⊙～5 M⊙)，而快速超新星爆炸模型恰好能拟合这段质量间隙。因此快速超新星爆炸模型更符合观测要求，而其他机制产生的致密星质量分布是连续的，不能较好符合致密星质量分布间隙，所以我们采用快速超新星爆炸模型计算最终形成的黑洞质量。

2.8 引力波辐射

双致密星绕转因辐射引力波而损失系统角动量，并缩短双星轨道间距。对于轨道间距较小的双黑洞，引力波辐射最终可能会导致双黑洞并合。我们的研究采用以下公式计算并合时标[91]。

双星系统为圆轨道(椭率e=0)时，并合时标表示为：

τ 的单位为a；P 表示轨道周期，单位为h；M 表示啁啾质量，Mtot表示双致密星的总质量，qBH=MBH2/MBH1, MBH1和MBH2分别表示两颗黑洞的质量，单位为M⊙。

若双星系统为椭圆轨道(椭率e/=0)时，并合时标表示为：

其中，

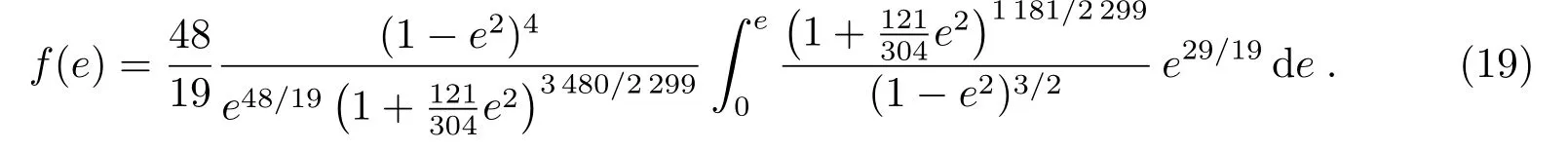
3 结果

我们研究了孤立的大质量双星系统通过稳定的物质转移通道，最终形成双黑洞。我们采用MESA 计算恒星演化，从主序前开始，直到恒星中心He 燃烧结束时停止；提取恒星质量及CO 核质量等参数，依据快速超新星爆炸机制计算出黑洞质量。我们的研究结果主要包括恒星初始质量与形成黑洞质量的关系，双黑洞的并合时标以及与观测研究的对比等。我们还发现，部分双星系统在第一次物质转移阶段中，次星因吸积物质而膨胀，最终次星充满洛希瓣，形成相接双星。其次，在MESA 程序模拟恒星演化过程中有部分双星系统程序计算不收敛，不能得到预期的结果，造成计算网格点数据不完整。第三，部分双星系统中恒星初始质量较小，恒星演化经历超新星爆炸，然后通过吸积回落物质形成黑洞；这种情况下形成的黑洞质量较小，在发生第二次物质转移阶段时质量比q2＞qlimit，会演化形成公共包层。这部分系统基本在中心H燃烧阶段或者赫氏空隙阶段进入公共包层，而研究表明在主序阶段或赫氏空隙阶段发生公共包层演化会导致双星系统并合[20]。

3.1 初始质量-终止质量

我们采用恒星演化程序MESA 计算双星演化，得到了恒星的CO 核质量以及形成的黑洞质量，图1a)给出恒星初始质量与CO 核质量关系，图b)给出恒星初始质量与形成黑洞质量关系，金属丰度在0.000 1 ～0.002 之间。我们只考虑形成黑洞的情况，形成中子星的情况不属于本文的研究范围。而初始质量为25 M⊙左右的恒星演化到中心He 燃烧结束时，形成的CO 核质量基本处于7M⊙～11M⊙之间，最终会通过超新星爆炸，再吸积回落物质形成黑洞。这种情况下，新诞生的黑洞会有反冲速度，大多数双星系统会被瓦解，只有少部分双星系统能保留，最终形成的黑洞质量小于直接坍缩形成的黑洞质量。

图1 初始质量-终止质量

恒星演化过程中金属丰度会影响恒星的星风物质损失率，从图1 中可以看出，金属丰度越高，主星最终形成的黑洞质量越小。次星形成的黑洞质量随金属丰度变化不明显，主要原因是次星演化过程中在第一次物质转移阶段会吸积大量物质，明显改变恒星的质量，吸积物质的质量不同，造成最终形成的黑洞质量差别较大。此外，在我们的结果中，大多数系统中主次星形成的黑洞质量会出现质量反转(初始质量大的恒星形成的黑洞质量反而较小)，随着质量比q1和恒星质量增大，反转效果越明显。图1b)初始质量与形成黑洞质量关系中存在几个黑洞质量明显较大的点(图中椭圆圈出部分)，主要原因是这些系统初始轨道周期较大，同时恒星质量较小，金属丰度较低，恒星演化膨胀不剧烈，第一次物质转移后轨道间距变得更大，后续双星演化过程中供给星没有充满洛希瓣，系统没有经历第二次物质转移阶段，次星演化到超新星爆炸前保留了更多物质，最终形成的黑洞质量也明显较大。其他质量系统没有发生这种情况，可能是因为其他系统初始轨道周期更小，初始质量更大，恒星金属丰度更高，恒星演化膨胀剧烈，能发生第二次物质转移。此外可能存在其他没有经历物质转移过程的情况，因为MESA 程序在计算过程中不收敛，导致没有得到相应结果。

我们将本文的计算结果与Belczynski 等人(红色线)[5]和Spera 等人(紫色线)[50]研究结果进行对比，如图1b)所示。他们的研究都采用快速超新星爆炸模型，计算了单星演化情况下恒星初始质量与形成致密星质量的关系。我们主要将主星演化结果与他们的研究结果进行对比，结果发现，在双星相互作用阶段供给星会损失大量物质，导致最终主星形成的黑洞质量整体处于Spera 等人[50]的结果下方。在小质量端，主星形成的黑洞质量小于Belczynski等人[5]的结果；在主星初始质量大于40 M⊙时，主星形成的黑洞质量大于Belczynski 等人研究给出的黑洞质量。快速超新星爆炸机制中计算致密星质量依赖于超新星爆炸前的恒星质量及CO 核质量，而不同研究者采用不同的星风物质损失模型、金属丰度以及CO 核计算模型，会导致计算得到的超新星爆炸前的恒星质量及CO 核质量存在差异，最终导致不同模型计算得到的致密星质量分布也不同。

3.2 并合时标

我们计算了形成的双黑洞通过引力波辐射损失角动量的并合时标，如图2 所示。模型只考虑稳定物质转移情况，不包含公共包层演化阶段，导致双星演化过程中缺乏有效缩短轨道间距的机制，并合时标强烈依赖初始轨道周期。如果初始周期太大，最终形成的双黑洞轨道间距较大，造成通过引力波辐射的并合时标远超过哈勃时标。只有初始轨道周期较小的情况下，形成的双黑洞才能在哈勃时标内并合(如图2，图中仅展示了并合时标小于哈勃时标的情况)。图中红色方块表示直接坍缩形成黑洞的情况，初始轨道周期越小，双黑洞并合时标越短：在初始轨道周期为3 d 时，最小的并合时标约为6 Ga；当初始轨道周期大于4.2 d 时，形成的双黑洞不能在哈勃时标内并合。蓝色方块表示通过超新星爆炸形成黑洞，这种情况下反冲速度可能使双星间距变小，最终形成的双黑洞最小并合时标约为0.5 Ga。恒星从零龄主序演化到形成黑洞的时标(约5 Ma)，远小于双黑洞辐射引力波损失角动量的时标，本文中并合时标是指从形成双黑洞开始到最终双黑洞辐射引力波损失角动量而并合的这段时间。

图2 初始轨道周期-并合时标

3.3 与观测对比

演化形成的双黑洞的质量分布如图3 所示，图中红色方块表示形成的双黑洞能在哈勃时标内并合，灰色点表示并合时标大于哈勃时标的情况。黑洞质量整体分布在(7 ～60)M⊙范围内，其中有个别情况形成的黑洞质量较大，最大约70 M⊙；系统的总质量分布在(15 ～110)M⊙范围内，双黑洞质量比整体分布在0.6 ～1 之间。其中小质量端和大质量端形成的双黑洞可能在哈勃时标内并合，而中间质量段的双黑洞并合时标都超过哈勃时标。我们将计算结果与目前已经探测到的引力波事件进行了对比，如图3 所示，图中带误差棒的点表示LIGO 和Virgo 探测到的引力波事件。从图中可以看到我们的模拟结果与探测到的部分引力波事件中的双黑洞比较相符，小质量端GW170608 和GW151226 与我们的结果符合得较好；在大质量端，观测点整体处于我们计算结果的下方，计算结果与观测样本符合不如小质量端好；在中间质量段(MBH1≈20 M⊙～35 M⊙)，形成的双黑洞总质量相对较小，由引力波辐射损失角动量导致的双黑洞并合时标相对较长，形成的双黑洞不能在哈勃时标内并合。

图3 双黑洞质量分布

由图4 可知形成的双黑洞并合时标小于哈勃时标情况下对应的初始主星质量-初始周期参数空间，蓝色方块表示通过超新星爆炸形成黑洞的情况，红色方块表示直接坍缩形成黑洞的情况。在小质量端，主星初始质量约为30 M⊙时通过超新星爆炸形成黑洞，新诞生的黑洞具有反冲速度，反冲速度会改变双星轨道间距及椭率，对应的初始轨道周期为3 ～5 d时，形成的双黑洞可能在哈勃时标内并合。在大质量端，主星初始质量大于60 M⊙，初始轨道周期为3 ～4.2 d 时，形成的双黑洞能在哈勃时标内并合。

图4 初始主星质量-初始周期

图5 展示了一个类似GW170729 引力波事件的形成通道，恒星金属丰度Z = 0.000 1，初始轨道周期为3 d，双星初始质量为(80+56)M⊙，主星在主序阶段充满洛希瓣，通过内拉格朗日点向次星转移物质，在3.6 Ma 后形成一颗质量为46 M⊙的黑洞，而此时次星吸积物质增长到69.9 M⊙。接着次星演化到主序末阶段充满洛希瓣，发生第二次物质转移，此时吸积星是黑洞，吸积率受爱丁顿吸积率限制，第二次物质转移阶段中黑洞只吸积了非常少的物质(约0.2 M⊙)，在4.62 Ma 后次星形成一颗质量为38.8 M⊙的黑洞。至此双星系统演化形成质量为(46.2+38.8)M⊙的双黑洞，通过引力波辐射损失角动量，最终双黑洞约在10.6 Ga 后并合。

3.4 讨论分析

之前已经有很多学者研究了孤立双星系统的演化，但是大多数研究都是基于快速恒星演化程序，这种程序的优点是可以快速产生批量的计算结果，但是对恒星详细的演化过程处理比较粗糙。我们在研究中采用一维恒星演化程序MRSA 模拟恒星演化，根据恒星结构方程，一步步迭代计算恒星演化，这样能比较准确地模拟恒星演化。但这会带来两个问题：(1)计算量大，所以计算速度慢且耗时长，导致计算样本数目不会太多；(2)演化过程中两颗子星都必须满足恒星结构方程，如果某一步不满足，MESA 程序会不停地迭代计算，直到最终时间步长非常小，计算结果不收敛，不能得到我们想要的结果，造成研究中网格点数据不完整。如图1，在大质量端，只有低金属丰度情况下，才能得到相应的计算结果；在金属丰度较高的情况下，程序会出现计算不收敛的问题，造成计算结果缺失。

图5 GW170729 可能的形成通道

超新星爆炸对双星系统的演化有重要影响，反冲速度越大越容易瓦解双星系统，Dominik 等人[20]的研究表明，减小反冲速度会增加双致密星并合率。我们在Fryer 等人的研究基础上取Vkick= (1-ffb)Wkick，在超新星爆炸形成黑洞的过程中，大部分双星系统会被超新星爆炸瓦解，只有少部分系统能保留。如果直接采用Hobbs 等人[72]的研究结果(即Vkick=Wkick)，不考虑回落物质影响，则几乎绝大部分经历超新星爆炸的系统都会被破坏。

第一次物质转移时双星质量比q2＜qlimit，是动力学稳定的物质转移。有一部分系统(主要在小质量端)通过超新星爆炸形成黑洞，这种方式形成的黑洞质量较小，在发生第二次物质转移时双星质量比q2＞qlimit，会演化形成公共包层；这些系统在供给星主序阶段或赫氏空隙阶段进入公共包层，有研究表明这种情况下公共包层演化会导致双星系统并合[20]。我们只考虑稳定物质转移通道，并假设进入公共包层演化阶段的系统最终都会并合。此外，有其他研究者认为在赫氏空隙阶段进入公共包层演化，系统最终可以抛射包层，双星不会并合，这种情况会增加双黑洞的并合率[5,20,42]。

双星系统通过稳定物质转移通道，不包含公共包层演化阶段，因此缺乏有效缩短轨道间距的机制，形成的双黑洞并合时标非常依赖于初始轨道。我们的模型提出，只有初始轨道周期较小的情况下(P0≤5 d)，形成的双黑洞才有可能通过引力波辐射损失角动量，最终在哈勃时标内并合；而对初始周期较大(P0＞5 d)的情况，形成的双黑洞都不能在哈勃时标内并合。

我们计算得到形成的双黑洞质量比分布约为0.6 ～1，其中大部分系统质量比都较大。大质量端能在哈勃时标内并合的系统，整体分布于观测点的上方(见图3)，可能我们选取的初始双星质量比较大，因此最终形成的双黑洞质量比较大。考虑较小的双星初始质量比，如果物质转移阶段双星没有相接，则形成的双黑洞质量比可能会较小。我们计算了部分初始双星质量比q1= 0.6 的样本，发现其中部分系统能发生稳定物质转移，双星不会在主序阶段相接，最终形成的能在哈勃时标内并合的双黑洞质量分布稍微下移了一点(如图3 中绿色加号)，但效果不是特别明显，整体依旧处于观测点上方。在较小初始双星质量比(q1＜0.6)的情况下，主序阶段发生物质转移的系统基本都会形成相接双星。

4 总结与展望

探测到引力波信号证实了恒星级大质量双黑洞的存在。我们采用一维恒星演化程序MESA 研究了初始质量为(20 ～80)M⊙，金属丰度分别为0.5%Z⊙,1%Z⊙,2.5%Z⊙,5%Z⊙以及10%Z⊙的大质量双星系统演化。在恒星演化到主序或者赫氏空隙阶段充满洛希瓣，通过稳定物质转移通道形成大质量双黑洞。金属丰度主要影响恒星的星风物质损失率，主要体现在主星的演化上，金属丰度越低，星风物质损失率越小，恒星演化形成的黑洞质量越大。研究发现，次星受金属丰度影响不明显，主要原因是次星在双星相互作用阶段会吸积大量物质，并明显改变恒星的质量，导致次星演化形成的黑洞质量差异较大。我们计算得到主星演化形成的黑洞质量分布在(10 ～55)M⊙之间。次星形成的黑洞质量受初始双星质量比的影响，初始质量比q1越大，形成的黑洞质量越大，分布在(7 ～70)M⊙之间。最终大质量双星演化形成的双黑洞总质量分布在(15 ～110)M⊙之间，系统质量比分布在0.6 ～1 之间。我们发现双黑洞并合时标主要依赖初始轨道周期，初始轨道周期≤5 d 的系统最终形成的双黑洞轨道间距较近，通过引力波辐射损失角动量，最终可能在哈勃时标内并合；如果初始周期大于5 d，最后演化形成的双黑洞轨道间距较大，并合时标远大于哈勃时标。研究结果能解释一些现在观测到的引力波事件，图3 给出我们的结果与探测到的引力波事件的对比，在小质量端GW170608 和GW151226 引力波事件落在我们的计算网格点中；大质量端与观测样本符合相对较差，观测点整体分布在我们计算结果的下方；中间质量段形成的双黑洞总质量较小，导致相同轨道间距情况下并合时标更长，最终系统不能在哈勃时标内并合。

我们工作中存在的问题是计算样本数目较少，下一步研究应该增加网格点密度，并选取更多的样本，包括目前工作中未涉及的巨星支阶段发生物质转移的情况；其次是反冲速度对形成双黑洞影响较大，后续工作可以研究不同反冲速度对形成双黑洞的影响；再次，在大质量端双黑洞质量比整体大于观测值，后续工作可以考虑更小的吸积效率以及更有效的角动量损失机制；最后，恒星的自转对恒星的星风物质损失以及内部混合等有影响，后续工作应该考虑恒星自转的影响。