太阳活动周的半球耦合研究进展

张小娟，邓林华

(1. 中国科学院 云南天文台，昆明650216； 2. 中国科学院大学，北京100049)

1 引 言

太阳是一个光谱型为G2V 的普通恒星，是宇宙中恒星大家族的普通一员，然而这颗普通的恒星是地球上生物赖以生存的能量源泉。太阳是距离地球最近的一颗恒星，是唯一可被高时空分辨率、高光谱分辨率和高灵敏度观测的恒星。太阳是决定人类生存的日地环境的母体，激烈的太阳爆发活动及一系列的日地空间效应对人类生存、地球气候和空间探测的环境有深远的影响。研究太阳表面大气上各种各样的磁活动结构的长期演化规律，是对日地空间环境中灾变事件给出预报和预警的重要途径之一。

Schwabe[1]首先发现太阳黑子的活动周期约为11 a，该周期被称为太阳活动的Schwabe周期。Schwabe 周期是描述太阳活动长期演化的一个重要特征，该周期是太阳内部磁场演化的结果。通过分析太阳黑子及相关现象的观测数据，Maunder[2]发现随着时间的演化，太阳黑子的纬度分布很像一只飞行的蝴蝶(即黑子蝴蝶图)，而且太阳黑子最先出现在太阳表面的中低纬度区域，随着时间的推移向赤道方向迁移[3]。Hathaway[4]编译了1874―2016 年的黑子面积的蝴蝶图及其长期变化规律，如图1 所示。由图1 可知，黑子在南半球和北半球各形成一个平行于赤道的带，在活动周开始时南北两个半球黑子群的平均纬度分布在±30°附近；随时间的演化向赤道方向迁移，太阳活动峰年的时候分布在±15°附近；然后随着时间的演化到每个活动周的末期时黑子群分布在±8°附近(Sp¨orer 定律)[3]。对于每一个太阳活动周，北半球和南半球的黑子分布不仅在时间上存在一定的相位差，而且在幅度上存在明显的不同，这种现象称之为太阳活动周的半球耦合[5]。

图1 太阳黑子的演化[4]

太阳活动周的半球耦合实质上是一种太阳磁过程现象。从太阳磁活动周期的观测研究历史发展脉络看，可从三个方面来描述该领域的发展：1)从形态上观测研究，20 世纪50 年代开始，对太阳黑子随太阳活动周的分布特征，以及谱斑、暗条变化等进行研究；2)对太阳纵向磁场进行研究，包括太阳综合磁图分析、大尺度磁场向赤道和极区演化以及活动区极性规则等；3)以大量活动区等矢量磁场统计观测为基础，对太阳磁活动周的变化进行研究。

从统计学的角度出发，对太阳活动指标(黑子数目、黑子面积、耀斑指数、日珥和暗条等)进行研究，发现南半球和北半球的磁活动在每个活动周表现出幅度不对称性和相位不同时性。在20 世纪中叶，太阳活动在南北半球上的差异性分布开始被人们关注。Newton 和Milsom[6]对黑子面积和数目在南北半球上的不对称性和不同时性进行研究之后，太阳半球活动的幅度和相位差异很快成为探索太阳活动周时空演化规律中的热门课题之一。可用三个阶段概括该领域的研究历程：1)从20 世纪50 年代初期到90 年代中期的猜测和确认阶段；2)从1995 年到2010 年的寻找演化规律的统计分析阶段；3)大约从2011 年开始的采用观测数据进行统计分析和发电机理论的数值模拟相结合的机制探索阶段。

太阳活动周的演化规律及驱动机制是太阳物理学重要的研究课题。作为太阳活动周的一部分，太阳磁活动的半球耦合特征具有相当重要的科学意义和应用价值。通过对太阳活动指标的统计研究以及对发电机模型的数值模拟，可以更加清晰地认识太阳活动的长期演化规律。本文第2 章将简单介绍太阳磁活动周的观测历史发展概况；第3 章将介绍太阳活动周半球耦合特征的表征方式；第4 章介绍太阳活动周半球耦合的观测结果与特点；第5 章综述太阳活动周半球耦合的发电机理论发展；第6 章对太阳活动周半球耦合领域仍未解决的科学问题及未来的发展方向进行讨论和展望。

2 太阳磁活动周的观测历史发展概况

早期的观测研究表明，宏观上，太阳黑子最先出现在太阳表面中低纬度区域，然后随着时间的推移，黑子会逐渐向赤道方向迁移，并且在太阳活动周期结束时，消失在赤道附近；但在这一个周期的黑子尚未完全消失时，下一个活动周的黑子又开始在中低纬度区域出现。长期的观测数据表明太阳黑子在时间- 纬度上的分布像一只飞舞的蝴蝶，Maunder 形象地称之为“黑子蝴蝶图”(见图1)[2]。

Hale[7]利用塞曼效应测量了太阳黑子中的磁场，并且于1919 年发现在双极黑子中，前导黑子的极性和后随黑子的极性在每个半球中是相反的(见图2)，这就是Hale 极性定律。在此基础上，延伸出了Joy 定律：在双极黑子中，后随黑子与赤道的夹角大于前导黑子与赤道的夹角，并且黑子所在的纬度越高，前导黑子相对于赤道的轴向倾斜角和后随黑子相对于赤道的轴向倾斜角均越大[8]。

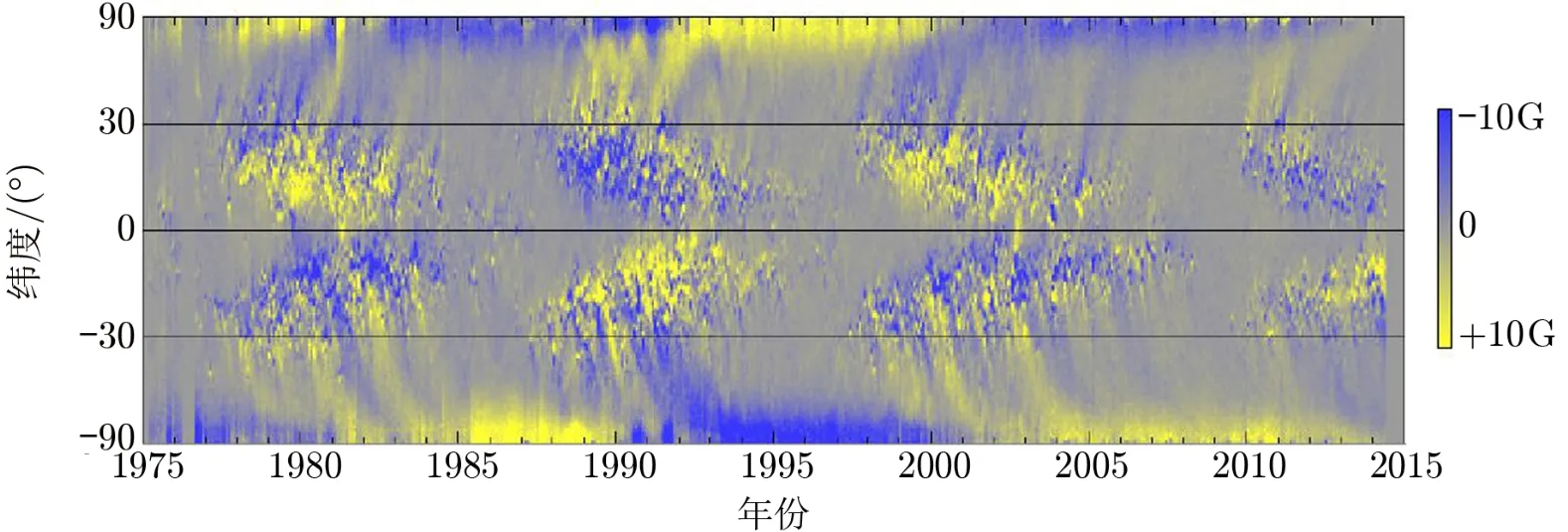
图2 根据Kitt Peak 和SOHO 仪器获得的纵向平均磁场蝴蝶图[4]

随着太阳磁场的发现，关于太阳活动周磁场的研究也逐渐出现。Bao 和Zhang[9]利用怀柔太阳磁场望远镜1988―1997 年的原始光球矢量磁图数据集，通过计算研究发现，北半球84%的活动区的电流螺度显示为负，南半球81%的电流螺度显示为正(半球螺度法则)；并且，平均电流螺度与太阳活动具有很好的相关性。然而，Hagino 和Sakurai[10]用Okayama和Mitaka 观测站获得的磁图数据，研究活动区中磁螺度的太阳周期变化，发现磁螺度的半球符号法则在太阳活动极小期的时候不成立。

Hao 等人[11]基于大熊湖太阳天文台的数据，研究了暗条在每个活动周中南北半球的不对称性，指出第22 个活动周中南半球为优势半球；而在第23 个活动周中，北半球占优势。Mazumder[12]对暗条倾斜角随时间变化进行研究后发现，在南半球存在正的暗条倾斜角，而在北半球暗条倾斜角为负，并且暗条总数和低纬度的暗条数量与活动周同周期地变化。

Komm 和Gosai[13]研究第24 个活动周的磁性特征，发现运动螺度遵循半球螺度规则：平均而言，北半球螺度为负，南半球螺度为正。Ouyang 等人[14]利用矢量磁图研究暗条的手征性和磁螺度，发现暗条的手征性在南北半球分布也是不对称的；并且统计结果显示北半球94.8%的暗条螺度为负，南半球87.4%的暗条螺度为正，由此可见活动区暗条螺度在南北半球的分布也是不对称的。

由以上研究可以了解到，人们在太阳磁活动的观测研究中，也逐渐发现了半球不对称现象，这为太阳活动周的研究带来了一些挑战和机遇。

3 半球耦合的表征方式

3.1 幅度不对称性的表征方式

太阳表面大气上的磁场活动随时间的长期演化可以用众多的活动指标来表征，例如黑子数目、黑子面积、耀斑指数、日珥和暗条、冕洞、日冕物质抛射等。统计研究表明，所有的太阳活动指标在北半球和南半球上的分布都不是均匀的。Maunder[2]是第一个注意到黑子面积在南北半球上的分布存在差异的科学家。Newton 和Milsom[6]最先对太阳活动不对称性进行了系统性的研究，他们使用的观测数据都来自格林威治天文台，并定义了半球分布的归一化不对称性(normalized north-south asymmetry index, An)，表达公式为：

此处，N 和S 分别表示太阳活动指标在北半球和南半球上的数值。自此之后，许多研究工作都是基于归一化不对称公式来开展。例如，Vizoso 和Ballester[15]研究了1874―1976 年间黑子面积的半球分布，发现太阳活动的不对称性具有统计学意义，意味着不对称性分布是一种真实的现象，而不是由随机抖动引起的；除此之外，他们还发现不对称性的程度与太阳活动并不是同相位的，在太阳活动极小期阶段这种不对称性特征表现得更加明显。Bankoti 等人[16]用归一化不对称指数研究了第20 至第23 个活动周多种太阳活动指标(黑子面积、活动日珥和Hα 耀斑)的半球不对称性后指出：北半球和南半球的不对称性特征具有相当高的统计学意义，而且这种半球不对称性是太阳活动中真实存在的特征。

然而，Ballester 等人[17]在利用离散傅立叶变换分析黑子面积周期特征的研究中，发现归一化不对称性的定义会引入Schwade 周期，在某些情况下容易产生误导性结论。他们认为绝对不对称性(absolute north-south asymmetry index, Aa)的定义更能反映太阳活动的半球分布，该定义的表达式为：

此处，N 和S 分别表示太阳活动指标在北半球和南半球上的数值。

为了研究太阳暗条半球分布在1919―1989 年间的长周期特性，Duchlev[18]提出了一种新的表达方式，即归一化的累积不对称性(cumulative normalized north-south asymmetry index, Acn)，表达式为：

此处，Nc和Sc分别表示太阳北半球和南半球的太阳活动指标的累加数值。在此基础之上，Li 等人定义了绝对的累积不对称性[19](cumulative absolute north-south asymmetry index,Aca)：

此处，Nc和Sc分别表示北半球和南半球的太阳活动指标的累加数值。

每一种表征方式均有优点和缺点。Joshi 等人[20]用归一化不对称指数研究软X 射线耀斑指数，发现南北半球不对称性在太阳活动极小期时表现得更加显著，但是Temmer 等人[21]指出绝对不对称指数在太阳活动极大期时表现得更加显著，因此绝对不对称指数和归一化不对称指数都有明显的局限性。归一化和绝对的累加不对称性指数对起始数值的依赖性很强，适用于研究长期的演化规律。图3 所示为半球黑子面积的四种表征方式的联系与区别，时间范围从1974 年5 月到2016 年9 月，从上到下依次为归一化不对称性、绝对不对称性、归一化的累加不对称性和绝对的累加不对称性。从图3 中很容易看出，b), c)和d)在1960 年左右有明显的突变，但a)在此时间段看不出明显的变化特征。

3.2 相位不同时性的表征方式

太阳活动在南半球和北半球上的演化进程是密切相关的，在时间和空间上的长期演化形成了典型的蝴蝶图形状。但是，在有些时候，两个半球上也会存在相位上的差异，例如，在蒙德极小期，太阳黑子仅在南半球出现，而北半球却近乎没有。在合理地解释太阳半球活动的异步机制之前，我们需要研究这种观测现象的各种统计特征。

通常来讲，太阳半球活动的相位不同时性研究是基于南半球和北半球时间序列数据的对比来开展的。例如，Mclntosh 等人[22]采用带有120 个月滑动窗口的互相关算法对黑子面积在过去130 a 的相位差异性进行了分析，结果如图4 所示。在图中，纵坐标是南北半球的相位差(单位为月)，如果该值大于0，表示北半球在该时间点领先于南半球；相反，相位差的值小于0 表示南半球在时间上领先。

通过交叉递归图(cross-recurrence plots, CRPs)和相位异步线(line of synchronization,LOS)工具，我们也可以得出半球相位异步性的表征方式。例如，Deng 等人[23]使用CRPs方法分析了过去140 a 半球太阳黑子面积的相位不同步特征。如图5 所示，该图显示了黑子面积的半球相位差，CPRs 图中的红色线表示LOS。从图中可以看出，LOS 位于主对角线附近，但明显与主对角线存在一定的偏差，意味着黑子面积的半球演化存在相位差异，时间范围为-20 ～30 月(即从延迟20 月左右到领先30 月左右，如图5b)所示)。

图3 太阳黑子面积半球不对称性的四种表征方式

图4 太阳南北半球黑子面积变化和相位差异[22]

图5 黑子面积半球相位差[23]

4 半球耦合的观测特征

4.1 幅度不对称性的观测特征

4.1.1 普遍性

大量的观测研究表明，太阳半球活动的幅度不对称性已被证实是一种真实存在的现象。光球表面的黑子、光斑和白光耀斑、色球上的暗条、日珥和Hα 耀斑、日冕中的日冕物质抛射和冕洞等太阳活动现象，都存在明显的幅度不对称性。例如，Roy[24]研究了1955―1974年间的剧烈耀斑时间、大黑子和小黑子、不同磁场类型的黑子，发现它们都存在半球的差异性分布。

人们将太阳半球活动的差异性分布按照不同的活动周来分开研究，同样发现在每个活动周都存在幅度不对称性，而且具有统计学意义。例如，Temmer 等人[21]研究了黑子相对数从第18 到第23 活动周的半球分布特性，发现在活动周的不同演化阶段，幅度差异性均存在。Li 等人[25]研究了1957―1998 年间活动日珥的半球不对称性，发现高纬度的日珥和低纬度的日珥都存在不对称性。

从以上研究可知，不同尺度的太阳磁场活动在不同层次、不同纬度、不同活动周上均存在幅度分布的差异性，因此可以说幅度不对称性是太阳表面普遍存在的一种观测现象。

4.1.2 周期性

幅度不对称性的周期性是研究人员重点关注的课题，因为这对于太阳活动和空间天气的预报有重要的实际意义。根据不同研究人员的定义，此处的周期可分为短尺度周期(小于11 a)、中等尺度周期(11 ～30 a)以及长周期(大于30 a)。

基于基特峰国家天文台(Kitt Peak National Observatory) 的光球磁场数据(1975―2003 年)，Knaack 等人[26]研究了太阳磁场南北不对称性的周期振荡，得到的显著性周期为320 ～329 d, (1.50±0.04) a, (1.79±0.06) a, (3.6±0.3) a, (43.4±7.1) a。基于同样的观测数据，Knaack 等人[27]还发现2.6 a 和1.3 a 两个周期，并认为这与中纬度区域(30°～55°)大尺度磁场的极向运动有关。值得注意的是，1.3 a 周期也存在于对流区底部的自转速率[28]、行星际磁场和地磁活动[29]、黑子面积半球不对称性等数据中[30]。

20 世纪80 年代，太阳峰年卫星(Solar maxium mission spacecraft)观测发现太阳X 射线暴和耀斑的振荡周期(Rieger-type variations)小于1 a[31]。Akioka 等人[32]指出，太阳黑子群数和太阳黑子面积有17 个月的活动周期特征。Badalyan 等人[33]通过对日冕绿线强度、黑子数目和面积、网络场磁通量的观测数据研究分析，发现准双年振荡(quasi-biennial oscillation, QBO，此周期的范围是0.6 ～4 a)在这些指数的半球不对称性中都存在，并指出这是幅度不对称性的一个基本属性，且有可能控制着太阳南北半球磁场产生机制的某些关键过程。随后，Badalyan 等人[34]发现，相比较南北半球的原始数据，QBO 在不对称性时序数据中更显著，他们还发现QBO 的相对功率谱与半球不对称性呈反相关。Chang[35]使用对数倒频谱分析方法研究了黑子面积半球不对称性的周期性，发现了9 a, 1.4 a, 3.8 a 和43 a等显著性周期。

4.1.3 扩展性

不仅太阳活动的幅度(强度)在两个半球上存在不对称性，太阳较差自转、太阳磁场极性反转的时间、太阳上的周期性振荡，子午环流速度等在南半球和北半球上的分布也存在着一定程度的差异。Shimojo[36]通过对第23 到第24 个活动周日珥数据研究发现，南北半球日珥活动的范围明显不同，McClintock 和Norton[37]发现Joy 定律中的倾斜角在南北半球中也存在差异性，Mazumder 等人[38]研究了暗条、极性反转线(polarity inversion lines, PILs)和冕洞，发现暗条和PILs 的半球不对称性与黑子面积的不对称性呈正相关。

太阳在不同层次上的自转特征，在南北半球上也会表现出明显的差异性。Zhang 等人[39]在2015 年研究了太阳黑子和软X 射线耀斑在1977―2012 年间的自转规律，发现南半球的转速稍微比北半球快一些。Xie 等人[40]研究了1945 年1 月到2010 年12 月黑子数据的时域变化，推测出北半球的自转在第24 个活动周的初始应该快于南半球。Vats 和Chandra[41]发现太阳自转在日冕层也存在不对称性，南半球在奇数活动周的自转比北半球快，在偶数活动周却是相反的。

研究表明太阳活动存在不同尺度的周期性振荡现象，而这些周期性振荡在南半球和北半球并不是严格对称的。Gurgenashvili 等人[42]对第19 到第23 个活动周的黑子数、黑子面积以及总磁通量进行研究，发现在第19 和20 个活动周，北半球有160 ～165 d 的周期，而在南半球存在180 ～190 d 的周期；在第21 到第23 个活动周，南半球存在155 ～160 d的周期，而北半球存在175 ～188 d 的周期。Deng 等人[43]指出色球耀斑活动的周期性振荡QBO 在南北半球上的分布也存在不对称现象，尤其是在每个活动周的极小期。

4.2 相位不同时性的观测特征

4.2.1 普遍性

研究表明，太阳半球活动在相位上存在不同时性，即半球演化存在一定的时间差。Waldmeier[44]发现相位的不同时性在光斑、日珥和日冕亮点中均有出现，并且指出相位差的长期变化存在周期性，周期为8 个活动周(约88 a)。

一个完整的活动周包括上升期、极大期、下降期。每个活动周的各个时期相位差也会有所不同。Norton 和Gallagher[45]通过对黑子数据的研究发现，上升期的半球相位差为0 ～11月，而极大期和下降期的半球相位差分别为0 ～14 月和2 ～19 月，相位随机分布在每个活动周的上升或下降的一半时间。Norton 等人[5]进一步研究发现太阳磁活动也有类似的结果，太阳磁活动的半球相位差在0 ～19 月之间变化，转化为太阳活动周期长度的15% ～20%(约为2 a)。Vernova 等人[46]通过对基特峰综合磁图(Kitt Peak synoptic maps)在1976―2003 年所记录的光球磁场南北半球通量的不平衡性分析研究，发现北半球在上升期占优势，但是在第21 ～23 活动周的下降期，南半球占优势。

众所周知，太阳磁场的极性在每个活动周的峰年反转，但是在南北半球上的反转时间是不同步的。Babcock 和Livingston[47]指出太阳南北两极的磁场极性反转时间不同，太阳南极的极性反转发生在1957 年中期，而太阳北极的极性反转发生在1958 年的末期[48]，并且指出磁场反转发生在太阳活动周的极大期附近(第19 个活动周的极大期在1957 年后期)。Svalgaard 和Kamide[49]指出强度较大的半球的极性反转是领先的，例如在第19 个活动周，南半球的极性反转早于北半球。

Li 等人[50]通过对耀斑数据的研究发现，北半球的周期平均值为10.7 a，南半球的周期平均值为10.1 a，这意味着Schwabe 周期在南北半球上的长度差异是导致南北半球相位不同时性的可能原因。Janardhan 等人[51]研究指出，在第24 个活动周，南半球的极性反转发生在2013 年中期，而北半球的极性反转在2012 年6 月就开始了。

从20 世纪80 年代(或者更早的时间)人们发现太阳活动在南半球和北半球不同时发生，到最近几年的研究具体到南北半球活动发生的时间差，表明南北半球太阳活动的相位差是普遍存在的。

4.2.2 周期性

相位不同时性的周期性对于空间天气的预报有着相当重要的作用，对此有很多相关的研究。然而，对于南北半球太阳活动不同时性的相位差，其计算结果对数据的长度以及研究方法有很强的依赖性。

Zolotova 等人[53]用CRPs 和LOS 技术[52]研究了过去300 年的黑子数据，发现相位领先的半球存在某种长期的演化趋势，其中1745―1783 年、1830―1877 年和1928―1968 年相位领先的半球都是南半球，其余时间相位领先的半球是北半球；此外，他们还发现，从1750 年开始，黑子活动的半球相位差与黑子演化的纬度分布呈反相关性。Murak¨ozy 和Ludm´any[54]使用活动周质心法研究了黑子群数据从第12 个到第23 个活动周的半球相位分布，发现北半球与南半球交替领先4个活动周，总体上呈现4+4 的周期模式，此周期接近于格莱斯伯格周期(Gleissberg period，约为88 a)。Deng 等人[55]用CRPs 技术研究黑子数据，发现北半球黑子在1874―1927 年间领先于南半球(即北半球太阳活动领先于南半球太阳活动)，1928―1964 年间南半球领先于北半球，此后到目前为止北半球领先于南半球。

Waldmeier[44]指出，半球相位不同时性的相位差包含8 个活动周。早期的数据分析结果认为这种长周期特点是4+4 的周期模式[22,53,54,56]，但有研究表明太阳磁活动的半球不对称特征存在一个12 个活动周的长周期行为[19,57,58]。而在最近的研究中，Deng 等人[23]用多种技术方法对黑子面积数据做了相关分析，发现相位不同时性存在8 个太阳周期的长周期特征，但是这种长周期特征呈现的是3 (南半球领先) +5 (北半球领先)模式。

南北半球活动相位不同性的周期依旧是一个有争议的研究课题，数据长度和研究方法的不同导致得出的结果不尽相同。

4.3 幅度不对称性与相位不同时性的联系与区别

Waldmeier[44]指出半球相位不同时性的相位差增强了半球的不对称性，两者存在明显的联系。Feng 等人[59]通过对耀斑指数的研究发现，太阳活动南北半球的不同步性和太阳活动南北的不对称性密切相关。Deng 等人[60,61]研究极区光斑的长期特性，发现其南北半球幅度不对称性和相位不同时性均不是随机现象，且这两种特征都是纬度的函数。这些研究都支持两者存在紧密联系。

但是，也有许多研究人员认为两者存在显著的差别。Zolotova 和Ponyavin[62]使用小波变换和傅里叶分析研究了LOS 的周期，发现了42.29 a, 18.52 a 和7.63 a 这3 个明显的周期，但不对称性指数的典型周期为43.29 a, 21.6 a, 14.41 a, 11.79 a 和8.64～9.26 a 等多个周期(见表1)，从图6 可以看出不同时性和不对称性的典型周期有显著区别。Li 等人[19]通过研究5 种太阳活动指数(黑子面积、群黑子数、暗条等)的半球演化规律，得出幅度不对称具有12 个活动周的周期，但是相位不同时性的特征周期是8个活动周，并指出幅度占优的半球并不一定是相位领先的半球。此外，Murak¨ozy 和Ludm´any[54]使用线性拟合方法研究了南北半球的相位差与强度差的关系，但没有发现任何正相关或反相关的潜在关系，这意味着两者的长期变化没有直接关联。

表1 LOS 和NA 的周期[62]

从上面的研究可以看出，不同的研究人员采用不同的分析方法或不同的数据来源，得出的结论有时是相互矛盾的，幅度不对称性与相位不同时性的相关性仍需进一步的研究。

5 半球耦合的物理机制

5.1 发电机模型

平均场电动力学在许多教科书和综述文章中都有很详细的介绍，本节对平均场湍流相关的内容做简单的介绍[3,5,63-66]。在太阳活动周的平均场和类平均场模型中，磁场的扩散衰减和传输都被认为是各向同性的(线性)扩散，扩散系数取值较大时，对流层中弥散的小尺度湍流耗散较多。

在平均场电动力学的框架中，磁场的传输对大规模磁场的影响实际上更复杂。平均场发电机方程式在尺度范围的基础上假设：磁场和磁场流视为大(均值)分量和小(湍流)分量，B=〈B〉+b′,U=〈U〉+u′，并且定义，〈u′〉=0 和〈b′〉=0。在这样的假设下，由MHD方程得到的均值归纳方程为：

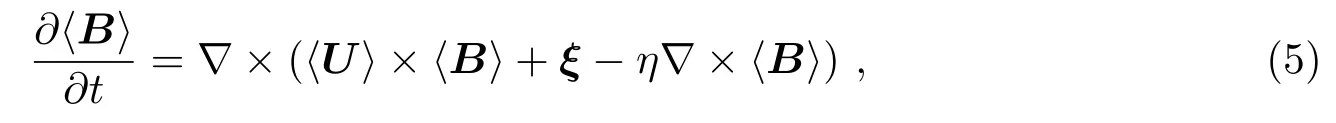
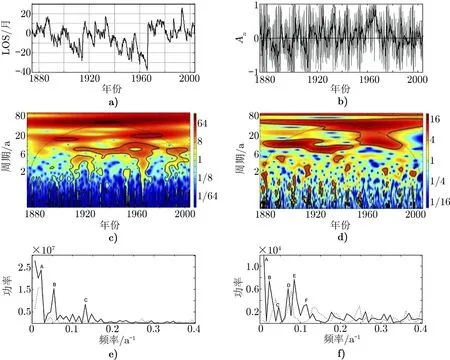
图6 半球幅度不对称性与相位不同时性[62]

此处，〈U〉×〈B〉是指大尺度磁场流运动产生的电动势，η 为磁扩散率(与等离子体的电导率成反比)，ξ =〈u′×b′〉为平均湍流电动势。根据平均磁场，该湍流电动势可以写为泰勒级数展开：

此处，张量α, β 等参数取决于流体性质(不取决于磁场〈B〉)。在此保留前两项，并将张量α 的对称和反对称部分分离为，则上述的泰勒展开变为：

此处，γi=-(1/2)εijkαjk，代入式(5)，γ 取决于大尺度流〈U〉 (被称为湍流泵浦，作为〈B〉的传输剂)，受〈U〉的影响；在近似均匀，各向同性的湍流中，和βijk的各向同性(对角线)的分量减小为：

并且，湍流泵浦与湍流强度梯度的关系为：

此处，τc为湍流的相关时间(通常被认为与对流周转时间相当)。此时，式(5)可以写为：

此处，张量α 的各向同性部分描述了与平均场〈B〉相对应的电动势；张量β 是磁扩散率η的累积效应，由式(9)可知β ≫η；但是在小尺度流的情况下，β 为〈B〉的传输和扩散的响应。这就是在太阳活动周研究中所有的平均场或类平均场模型中引入的湍流扩散。

值得注意的是，在非线性近似的情况下，洛伦兹力J ×B 的存在会对速度有影响。类似的，在J =〈J〉+j′的情况下，我们可得到：

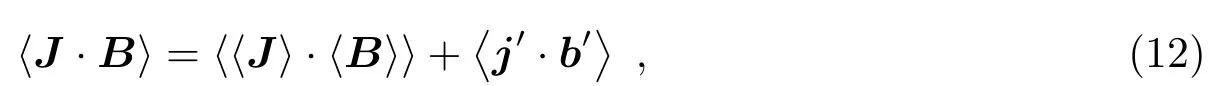
在平衡态下，〈J ·B〉=0，则有，

经过计算我们可以得到(详细公式推导计算过程见文献[65]中的第6 章和第10 章)：

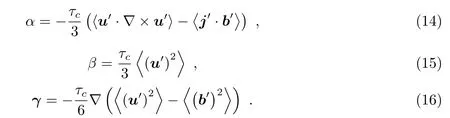
由式(14)可知，α 效应具有动力学和磁场两部分的贡献，湍流扩散不受小尺度磁场波动的影响，但是湍流的反磁效应受磁波动的影响，对均分磁场有消弱作用。此处的波动速度和磁场是实际的磁场，不是“原始”湍流的磁场[65]。

5.1.1 平均场发电机模型

在太阳活动周经典的平均场模型中，环形大尺度磁场由太阳的较差自转产生，极向场主要由湍流电动势产生。但是在太阳发电机理论中，附加磁场源项也会出现，在流量和张量大尺度范围的情况下，式(11)会变成线性方程，特征解的模式为∝exp((σ+iω)t)。最低奇数(偶极)和偶数(四极)本征模的增长率σ 通常相似，高扩散率通常有利于最低本征模(通常为偶极)，而四极子午流的主导输运通常倾向于四极本征模。偶极和四极解共存的趋势可以在非线性机制中持续存在，并且本身会导致半球不对称性和随之而来的磁周期幅度调制[67]。

在解方程时引入非线性效应可以产生对称(偶)模型和反对称(奇)模型、强半球不对称性以及极小期时期的特殊现象。Kleeorin 和Ruzmaikin[68]根据线性特征向量上磁场扩展的幅度，推导了一个非线性常微分方程组，在偶极子和四极子中考虑非线性解，发现在四极子模式弱于偶极子模式的假设前提下会出现周期不同步的现象。Tobias[69]指出，当环向场弱的时候会出现对称破缺，即会有不对称的现象产生。

Brooke 等人[70]指出，轴对称发电机模型的时间周期解可以解释极小期以及赤道对称性破坏的现象，另外，在模型中引进随机波动(如平均场的α 效应或者子午环流速度)也会导致半球不对称以及在时间上激发高本征模和混合模式的解。Olemskoy 和Kitchatinov[71]使用时间和纬度的平滑变化随机函数将波动的极向场的源项引入平均场发电机模型，发现波动违反了发电机场的半球对称性，当偶极子奇偶校验的偏差很大时，该模型显示出弱磁循环，其中磁活动不对称性通常表现为黑子活动极小期。

Sch¨ussler 和Cameron[72]指出，具有弱驱动的Babcock-Leighton 发电机模型在恰当的周期范围内会产生激发的偶极模式和阻尼四极模式，极向场源的随机波动和四极模式的随机激发会导致太阳活动的不对称性。在包含随机波动效应的非线性情况下，Sch¨ussler 和Cameron[72]给出极向场源的径向积分的环形磁通量对称(图7a)为四极)和反对称(图7b)为偶极)结果。

图7 环形磁通量的时间-纬度图[72]

5.1.2 随机波动效应

在平均场发电机模型中，通常考虑的是α 效应和子午环流，大范围的子午环流是由全球速度场产生的，当这个速度和弱的半球耦合流相关的流动速度低于湍流速度时，就会比较容易产生波动[73]。平均场的α 效应中波动的起源是基于相同的原理，另外，由于双极太阳活动区的倾斜角分布变化很大，因此在Babcock-Leighton 模型中也会出现显著波动。这种类型的建模方法所对应的波动在不同纬度和不同半球上是不相关的，可以产生半球的非对称解。

Passos 等人[74]通过使用平均场发电机模型，在两个半球引入独立的随机波动来研究半球不对称和周期幅度调制的起源，发现平均场α 效应在太阳活动周极小期上升阶段中有很重要的作用，并且展示了许多类型的半球不对称性；在此研究结果基础之上指出，太阳活动可以表现出显著的半球不对称性。此模型的计算模拟结果：αMF=0.4 (100%)、αBL=21.0(25%)，半球相位滞后在半球中不同时出现[74]，如图8 所示。

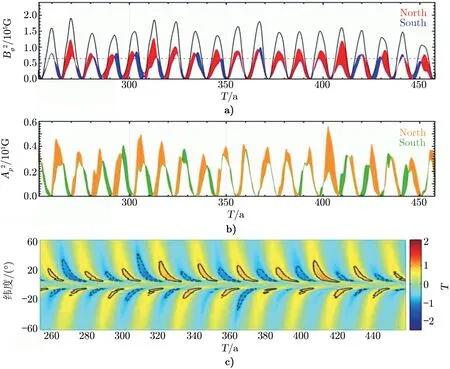
图8 Norton 得出的数值模拟结果[5]

5.1.3 非运动平均场模型

Sokoloff和Nesme-Ribes[75]指出，磁场的不均匀旋转引起的宇称解可以解释半球不对称性，在混合奇偶解中，偶极子和四极子可以相互作用，从而导致半球的不对称性。Tobias[69]得出相似的结论，并且指出当发电机弱场解(如极小值)时，相关的不对称性仅由混合宇称解引起，Malkus-Proctor 效应对偶极强场解的不对称性具有更深远的影响。

Pipin[76]考虑了弱非线性αΛ 平均场，该模型产生的解表明，对角动量通量的磁反馈会产生类似于太阳黑子格莱斯伯格周期(Gleissberg period)，半球活动的不对称性是因为宇称解的奇偶性被破坏(和较差自转的对称性有关)。

5.1.4 全球对流发电机模型

在全球对流发电机模型中，大型的磁场在空间和时间尺度上的演化比对流本身更长更大，如此大规模的磁场随着时间的演化发生极性反转，存在很明显的半球不同步性和不对称性。Brown 等人[77]计算了半球不同步性和不对称性的短周期(约几年)。Passos 和Charbonneau[78]模拟了时间跨度为1 650 a 的活动周(见图9)，并且分析了半球的统计特征。

图9 Norton 在文献[78]研究方法基础上得到的数值模拟结果[5]

5.1.5 磁场耗散

Charbonneau[79]认为跨赤道的磁场耗散是半球耦合的主要机制。发电机理论的数值模拟结果说明磁场耗散(甚至是湍流耗散)可能是半球耦合的主要机制；在实际的数值模拟中，具体的耗散比较复杂，对于相关深度函数的实现以及模型中耗散的影响还没有很好的解释。在横向延长的对流细胞(又称“banana cells”)中，磁通量可以从一个半球混合到另一个半球，这有助于理解半球耦合机制[78]，详情见图9。

综合之前的研究工作可以发现，越接近磁场表面磁场耗散速率越大。在太阳周期的下降期，位于赤道平面两侧的两个环形系统，在纬度±8°处达到峰值，对应的线性距离为L ≃0.07R⊙，所对应的耗散时标为τ = L2/β，此时标所对应太阳活动周期约为10 a (耗散率为β ≃1013cm2·s-1)。对于超过该值的湍流扩散，所对应的跨半球耦合作用的扩散时标要比循环周期的时标短，即表现出强耦合作用；相反，对于低于该值的湍流扩散，所对应的跨半球耦合作用的扩散时标要比循环周期的时标长，即表现出弱耦合作用。在弱耦合的情况下(耗散较小时)，会产生半球耦合现象。

Chatterjee 和Choudhuri[80]在Babcock-Leighton 磁通量传输模型的基础上，研究MHD方程组的解并发现，子午环流在半球幅度之间有所不同(1%的差别)，但半球之间即使是这种微小的差异，也可能引发持续的相位滞后或明显的半球周期不同步现象。

5.1.6 螺度

螺度通常用来表示场线的几何拓扑性质，描述矢量场的螺旋性、场线的嵌套性等拓扑结构。在一个完整的电磁场系统中，磁螺度、电流螺度和能量，三者并不是孤立的物理量，磁螺度在太阳活动周的磁场演化中起着重要的作用[81]。

早期的观测数据建立了半球螺度规则：活动区的磁场在北半球优先显示为负的磁螺度，在南半球则显示为正的磁螺度[9,82-86]。然而也有一些研究人员认为，大规模(全球) 轴对称磁螺度在北半球为正，在南半球为负[87-90]。Pipin 和Pevtsov[91]通过对MDI (Michelson Doppler Imager)/SOHO (Solar and Heliospheric Observatory)数据分析之后，发现第23 个活动周的全球磁场在北半球的磁螺度为正，在南半球的磁螺度为负，且北半球和南半球的磁螺度是不对称的。

Yang 等人[92]在轴对称发电机模型的基础上考虑了磁螺度守恒的非线性效应，发现磁螺度的不平衡随着大尺度磁场的奇偶性而变化，并且指出α 效应和磁螺度的随机波动有着很重要的作用，即磁螺度的不平衡性可以破坏磁场的平衡性；小尺度的净磁螺度遵循大尺度净磁螺度的演化，但在时间上具有一定的延迟。

Zhang 等人[85]通过对矢量磁场数据进行分析，得出近两个周期的电流螺度的维度-时间图，并且指出螺度像黑子一样均向赤道方向漂移；与黑子极性不同的是，每个半球的螺度的符号不会在周期之间发生改变。由图10 可知，电流螺度与太阳活动周有关，并且遵循黑子的Hale 极性定律，但是又更为复杂[93]，即发电机理论产生的磁场是镜像不对称的。Kleeorin 等人[94]以及Zhang 等人[95]也得到类似结果。

图10 太阳活动区电流螺度特性时间-纬度蝴蝶图[93]

5.1.7 子午环流

在Babcock-Leighton 发电机模型[96-98]中，磁场传输是通过位于每个半球的子午环流实现的(即南北半球各有一个子午环流胞)，在这种情况下，北半球和南半球可以在某种程度上解耦[99,100]。Li[101]指出，太阳活动现象是由两个不同的耦合过程造成的，即每个半球有自己独立的演化系统。随后，Deng 等人[102]研究耀斑指数的南北半球幅度不对称性和相位不同时性，指出南北半球的磁场演化系统几乎不具有联系，此前Antonucci 等人[103]及Henney和Harvey[104]也有得出类似的结果。

Karak 和Choudhuri[105]用太阳黑子周期的通量传输模型研究Waldmeier effect (太阳活动周的上升时间与其强度反相关)，指出模型中太阳黑子活动周期不规则是因为受到极向场在生成过程中的波动和子午环流中的波动影响。Nandy 等人[106]的研究表明，子午环流不仅在极区磁场的演化中起着重要的作用，还影响着一个活动周周期的具体时间。而且，McIntosh 等人[22]指出，北半球和南半球之间磁场演变的相位差是南北半球不对称子午环流的结果。Belucz 和Dikpati[107]指出，太阳磁活动的半球不对称性取决于两个半球中子午环流幅度的差异。Shetye 等人[108]利用磁流管发电机模型证明，一个半球活动区流量相对大时，半球活动会相对强一些，即半球间子午环流的变化会影响半球的活动强度。

众多的研究表明，子午环流在太阳活动的半球耦合中扮演着重要角色。子午环流可以在两个半球中独立起作用，但子午环流的具体位置不清楚。Zhao 等人[109]用SDO/HMI 的观测资料进行研究并发现，双胞子午环流剖面的赤道流比之前认为的要浅(见图11)，这一发现表明我们需要对太阳磁场的产生和重新分布方式进行新的探索。

5.2 日震学对发电机理论的创新与约束

图11 子午环流剖面图[109]

我们知道，波在不同介质中传播特征是不同的。地震波可以用来研究地球内部的结构，日震学是基于地震波原理用以研究太阳内部结构的有效方法，即我们可以通过观测太阳表面的大气振动，来推断太阳内部结构的物理性质。日震学不仅让人们对太阳有了更清楚的认识，也加强了我们对太阳内部的了解，更是推动了太阳动力学的发展，为太阳动力学演化的研究开辟了新天地。

人们对全球日震学研究主要取得了以下成果：确定了太阳内部较差自转轮廓，发现了差旋层的存在；发现了大尺度子午环流和带谐流的存在；进一步确定了对流层底部存在的位置；发现了太阳振动的频率随太阳活动周的变化等[110]。这些成果在一定程度上冲击了传统发电机模型，例如，在对流层中，太阳自转速度对深度的依赖性较小，但是传统发电机模型需要自转速度随深度的变化。GONG (global oscillation network)观测到太阳振动中阶模式平均频率随太阳活动周的变化(见图12)，从图中可以看到强磁场区域的太阳振动中阶模的平均频率较高，而且太阳振动频率随太阳活动周的变化也有类似黑子蝴蝶图的效应[111]。

图12 Broomhall 等人[111]基于GONG 数据的研究结果

随着高分辨率望远镜的投入使用，人们在局部日震学中考虑将太阳的经度、纬度和太阳中心到表面的距离(即深度)作为可变量，用此3 个可变量来研究太阳内部的三维结构特征，使研究太阳表面局部特征和南北半球的不同结构以及各种流场成为可能。局部日震学通过分析局部区域振动信号，不仅可以研究三维流场、热与结构的不均匀性，还可以探究磁场本身。日震学研究已在太阳物理上取得了一些成果：研究太阳黑子光球下的速度场，探测黑子的浮现过程，用远端成像来推测太阳背面的信息。除此之外，通过日震学研究双层子午环流得出的结果对发电机理论也产生了一定的影响[111]。

6 未来的研究方向

数值模拟产生类太阳磁循环,模拟一些长周期的特性，但是在太阳活动周南北半球周期的不同步性和幅度的不对称性研究方面，模拟结果与观测结果并没有做广泛的比较。观测结果显示，太阳活动周的幅度不对称性和相位不同时性在一定的范围内产生。对于第17 ～23 活动周而言，半球黑子面积的幅度不对称性不超过20%；根据皇家格林威治天文台的太阳黑子数据可以确定，相位延迟的时间不超过太阳活动期的20% (约2 a)。

在过去的几十年里，相关专家对南北半球耦合现象已经做了大量的研究，太阳发电机理论也有了一定的发展，但在一些方面需要继续加强研究。

(1)如何改进提升太阳内部双子午环流现象的计算。

(2)更好的发电机模型应该结合极向场强源的实际值和精确位置，清楚解释除了11 a 的周期长度之外，为什么活动区的磁螺度在北半球显示为负，在南半球显示为正。

(3)在发电机模型中，差旋层对太阳活动周南北半球幅度不对称和相位不同时现象起着什么样的作用。

(4)发电机模型数值模拟的计算量以及参数的设定该如何根据现有的统计分析结果结合物理意义去设定。

(5)太阳活动指数在不同活动周上幅度占优和相位领先的半球是否被某种系统性的演化模式调制。

(6)对于太阳磁周期的起源，现有的发电机理论还需要怎样改进才可以精确地对未来太阳活动周做出更好的理解或者预报。

致谢

在本文的撰写过程中，感谢张枚老师、杨尚斌老师以及王华宁老师，硕士研究生一年级期间在北京学习《现代太阳物理导论》，他们在课堂上传授的知识对本文的撰写有很大的帮助。同时，特别感谢审稿专家对本文提出的建设性建议，从而使得本文内容更加全面充实，文章整体更加有深度。