银河系薄盘形成对核球的动力学影响

张骏凯，沈俊太3,，周颖颖

(1. 中国科学院 上海天文台 星系与宇宙学重点实验室，上海200030； 2. 中国科学院大学，北京100049；3. 上海交通大学 物理与天文学院 天文系，上海200240)

1 引 言

大部分旋涡星系由三部分组成：看不见的暗物质晕，扁平的盘和中心核球。我们的银河系也具有这三部分。银河系的核球贡献了25%的光度，拥有(1.2 ～1.6)×1010M⊙，因此银河系核球对于研究银河系的形成与演化具有重要的意义。银河系核球中，约99%的恒星年龄大于5 Ga[1]，并且有着广泛的金属丰度[2-4]。大核球在多个方面与椭圆星系类似，经典的核球理论认为核球因星系间的碰撞与并合形成。但是，此理论并不完整。Kormendy[5]在1993 年提出，一些核球具有类似盘的动力学性质，应该由盘星系经过长期的内部演化形成。

伪核球主要分为两种：一种是气体受到非轴对称结构(如棒)的影响，内流形成的扁平结构；另一种是在侧向棒旋星系看到的结构。当棒从盘上形成以后，棒在垂直盘的方向弯曲，经过加热形成了在侧向看到的盒状结构[6-8]，而银河系也拥有这样的盒状核球[9-11]。

Blitz 和Spergel[12]在1991 年利用视觉效应解释了银河系中心核球呈现出的非对称性:银河系中心具有长条形的棒，棒离我们近的部分看起来较大，离我们远的部分看起来较小。2008 年，Howard 等人[13]对M 型巨型星的核球视向速度(BRAVA)测量显示，在不同高度处的速度近乎相同，这意味着核球是像圆柱体一样旋转的。而McWilliam 和Zoccali[14]、Nataf 等人[15]2010 年在中心核球区发现了垂向的X 形结构。Wegg 和Gerhard[16]在2013 年测量了核球的三维密度分布，并观测到核球中心具有花生状结构，算出核球主轴与视线方向夹角为θbar=27°±2°。Wegg 等人[17]在2015 年发现花生状核球向外连续地转变为扁平的棒，其半长轴为(5.0±0.2) kpc，夹角为θbar=28°～33°。

基于伪核球理论的模型也很好地符合了观测上的结果。Shen 等人[18]在2010 年基于核球视向速度的研究(BRAVA, Rich 等人2007[19], Howard 等人2008[13])，提出银河系核球主体为侧面看到的棒，经典核球成分不超过8%。Saha 等人在2012 年[20]继续Shen 等人[18]的研究工作，发现经典核球质量较小时，也会旋转并在其内部形成类似棒的结构。Li 和Shen[21]在2012 年，发现Shen2010[18]模型具有类似观测到的X 形结构，而经典的核球很难解释这样的X 形结构。Martinez-Valpuesta[22]在2013 年使用具有初始径向金属丰度梯度的多体数值模型，解释了Gonzalez 等人[23]2011 年发现的盒状核球垂向金属丰度梯度。Debattista 等人[24]2019 年在类银河系的宇宙学模型中，也能定性地匹配现有的银河系核球的观测数据。

这些研究工作表明，银河系核球的主体很可能是侧面看到的棒，而不是经典理论中由星系并合形成的经典核球。核球形成的时间在星系演化早期，而后续来自晕的气体吸积在星系薄盘处形成的新恒星对已经存在的核球是否会造成比较大的动力学影响，仍是一个有待解决的问题。

在模拟星系盘中新恒星形成的问题上，同时包含气体与恒星模拟的模型运算量远超过只模拟恒星的模型。这种复杂模拟，不仅模拟了无碰撞的恒星，还模拟了气体冷却、径向加热、激波、内流、恒星形成、能量反馈到气体物质等。模型中模拟的许多过程发生在尺度较小的范围，大尺度上可以忽略。而对于恒星的形成与能量反馈部分往往依赖于很多亚网格物理过程，在具体的数值模拟过程中只是简单地采用一些特殊规则模拟这些过程。更重要的是，激波驱动的气体内流在棒内对数值黏性非常敏感[25]，需要高精度的模拟。Sellwood和Moore[26]在1999 年采用了更加简洁高效的数值模型，仅对大尺度上盘的动力学演化影响较大的两个气体过程(气体耗散和气体在棒的内流)进行简化处理，而忽略了其他的气体过程。动力学上需要的只是稳定地减少粒子的均方根速度，以维持系统的演化。通常温和的旋臂激波对气体流线的形状影响很小，气体转化为恒星的过程不会显著地改变气体原来的圆周运动轨道，因此他们在盘上直接添加做纯圆周轨道运动的粒子并模拟盘的形成。本文沿用了这个模拟盘形成的办法，在Shen 等人[18]2010 年的模型基础上，考虑薄盘的形成，以研究在棒形成以后，薄盘上形成的新恒星对核球的动力学影响。

2 模型设置

我们采用了Shen2010[18]的多体数值模拟模型，采用1×106个粒子来模拟原初盘，以在高密度的核球区得到较高精度的结果。模型中初始只包含一个刚性等温暗晕和一个薄指数盘作为原初盘。为了集中计算能力来研究盘的演化，这里不使用由粒子构成的暗晕，而仅仅采用暗晕的势场。这里Vc= 250 km·s-1是该势场下无穷远处的圆周轨道速度，Rc= 15 kpc 表示势场的核心半径，在这个半径之内势场几乎不变。模型中采用1.9 kpc 和0.2 kpc 作为初始盘的标长和标高。原初盘是一个指数盘，质量为Md=4.25×1010M⊙，大约为截止半径Rd=9.5 kpc 内的星系总质量(含暗物质)的55%。

由于原初盘的不稳定性，棒很快会在盘面上形成。接着由于屈曲不稳定性，棒在垂直于盘面方向发生弯曲，饱和之后形成盒状核球。在大约2.4 Ga 以后，棒稳定地在盘面上旋转，此时棒的半长轴大约为4 kpc。我们的研究目标主要集中在薄盘上新形成的恒星对核球后续的动力学影响，较长的薄盘恒星形成时间会使我们难以区分不同时刻形成的薄盘恒星对核球的影响，所以我们选择了较短的薄盘恒星形成时间(2.4 ～3.0 Ga)，并继续运行至4.8 Ga，以得到这些薄盘恒星对核球的动力学影响。为了区分讨论2.4 ～3.0 Ga 新添加的恒星和星系中原有的恒星，分别用薄盘和原初盘指代这两类恒星。薄盘恒星由晕上冷却在薄盘上做圆周轨道运动的气体坍缩形成。气体在转化为恒星的过程中，其轨道不会发生明显的变化[26]。因此我们在薄盘上缓慢地添加初始轨道为纯圆周轨道的粒子以模拟薄盘上新恒星的形成，每个粒子的质量为4.25×104M⊙。模型省略了星系晕上气体冷却被星系盘吸积，以及这些气体在薄盘上形成新恒星的过程，因此整个过程中星系盘质量不守恒，随着时间缓慢增长。因为这些新恒星的总质量相对星系晕质量较小，整个模拟过程中可以近似认为星系晕质量不变，并利用刚性等温晕的势场来模拟星系晕，而并未引入粒子模拟星系晕。Li 等人[27,28]在2015 年和2016 年研究了棒对气体盘的影响，发现气体会受到棒的影响损失角动量而内流。但是气体盘质量远小于棒的质量，棒从气体盘中获得的角动量很小，所以我们的工作中忽略了气体盘的模拟，以减少模型的计算复杂度。模型中薄盘的初始半径Ri由按高斯分布的随机函数决定，其中R 为添加薄盘恒星的中心半径。为了后续能研究不同薄盘中心半径对银河系核球的动力学影响，薄盘恒星的初始半径高斯分布弥散不能设置得过大，以至于覆盖到整个银河系盘或者核球区；也不能设置得过小，导致局部密度增加过快。原初盘的初始截断半径为5 个标长，因此我们将薄盘恒星的初始半径高斯分布弥散设置为2 个标长(σ = 3.8 kpc)，对应的初始速度为纯圆周速度

薄盘恒星在添加入模型中以后，其动力学性质会在棒非对称势场的影响下发生变化。通过比较不同添加薄盘恒星的中心半径R 和恒星形成率SFR 的模型，我们可以得到薄盘恒星在不同情况下对核球区的动力学性质的影响。这些模型中，我们依次挑选了从棒附近到外盘范围的几个位置作为其添加薄盘恒星的中心半径。观测上对银河系恒星形成率的测量基于全局的观测。Smith 等人[29]在1978 年通过对HII 的测量，间接地得到O 型和早期B 型恒星数量，进而得到恒星形成率为5M⊙·a-1。在Benjamin 等人[30]2003 年对银河系中心盘面上的年轻恒星数量的研究基础上，Robitaille 和Whitney[31]通过分析星族合成模型得到了银河系总体的恒星形成率为0.68～1.45M⊙·a-1。模型中薄盘恒星的形成时间较短(2.4～3.0 Ga)，较小的恒星形成率不会引入足够薄盘恒星，从而不能影响质量较大的原初盘，因此我们选取了1.77～17.7M⊙·a-1的恒星形成率。表2 列出了本文使用的模型的主要参数。模型采用添加薄盘恒星的中心半径R和薄盘的恒星形成率SFR进行命名，如添加薄盘恒星的中心半径为4 个初始尺标长度(1 个初始尺标长度为1.9 kpc)，薄盘恒星形成率为5×1.77M⊙·a-1的模型将被命名为G45，而作为对比的Shen2010[18]模型(无薄盘)则被命名为G00。

表1 模型主要参数说明

3 模型的演化过程

3.1 模型演化的动力学图像

图1, 2, 3, 4 是模型G45 分别在2.7, 3.0, 3.3, 4.8 Ga 的不同时刻原初盘和薄盘的位置速度分布图。其中模型G45 的薄盘位置参数为4 个尺标长度(1 个尺标长度为1.9 kpc)，恒星形成率为8.85M⊙·a-1，在2.4～3.0 Ga 的时间内添加了相当于原初盘质量约12.5%的薄盘恒星，其余时间不添加薄盘恒星。薄盘恒星和原初盘恒星呈现出了不同的位置速度分布。薄盘恒星出现了明显的旋臂结构，而原初盘恒星随着薄盘恒星的不断加入，在棒的外部也出现了模糊的旋臂形状。薄盘上新形成的恒星冷却了星系盘，使其产生“振荡放大”不稳定性，从而出现暂现但可重复被激发的旋臂结构[32]。

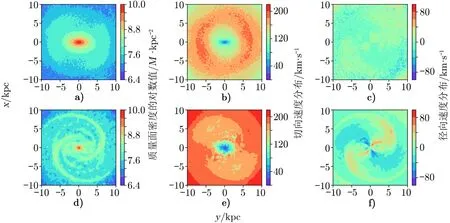
图1 G45 模型在2.7 Ga 时刻原初盘和薄盘的位置速度分布图

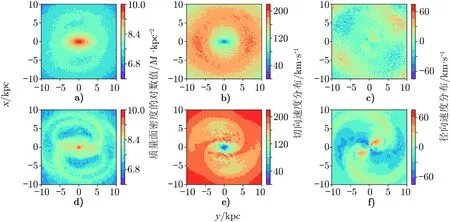
图2 G45 模型在3.0 Ga 时刻原初盘和薄盘的位置速度分布图

图3 G45 模型在3.3 Ga 时刻原初盘和薄盘的位置速度分布图

图4 G45 模型在4.8 Ga 时刻原初盘和薄盘的位置速度分布图

原初盘恒星的切向速度分布图在盘处大致呈环状，说明大部分原初盘恒星轨道依然是玫瑰花型；但是在棒两端由于势场较深，这些原初盘恒星具有较大的切向速度。薄盘恒星的切向速度分布图在盘处随着时间的推移逐渐出现旋臂形状，这些薄盘恒星通过与旋臂或者棒交换角动量损失速度，向棒区迁移。径向速度图像上，薄盘恒星呈现出了明显的向棒区移动和远离棒区的部分；这说明这些恒星的轨道逐渐由玫瑰花型轨道变成支持棒的x1 型轨道，发生了迁移。x1 型轨道指在与棒共转的坐标系下，沿着棒主轴运动并且构成棒骨架的狭长型周期性轨道[33]。模型在2.4～3.0 Ga 不断添加薄盘恒星的过程中，迁移特征越来越明显。在3.0～4.8 Ga 不再添加薄盘恒星的时候，迁移特征没有很快消失，而是先在3.3 Ga 时刻变得更加明显，随后逐渐消失。

3.2 薄盘恒星的位置分布

随后，我们对薄盘恒星的位置分布情况进行了研究。图5 显示了模型G45 中新恒星的初始位置分布，以及在4.8 Ga 的位置分布情况，从中可知新恒星半径方向的分布由原来设置的单峰高斯分布变成了双峰分布，且初始分布的中心位置处的新恒星数量变少。这些新恒星沿着盘半径方向的位置分布发生了变化，一部分被棒捕获进入银河系中心，而另外一部分向外迁移；垂直盘面的方向z 的分布由窄变宽，这些新恒星在逐渐加入薄盘时，受到星系中较厚的原初盘势场的影响而被加热，使得薄盘略微增厚。但是与经历过星系演化早期棒的形成过程而被增厚的原初盘相比，后续添加的薄盘被加热后依旧较薄，标高约为0.5 kpc。

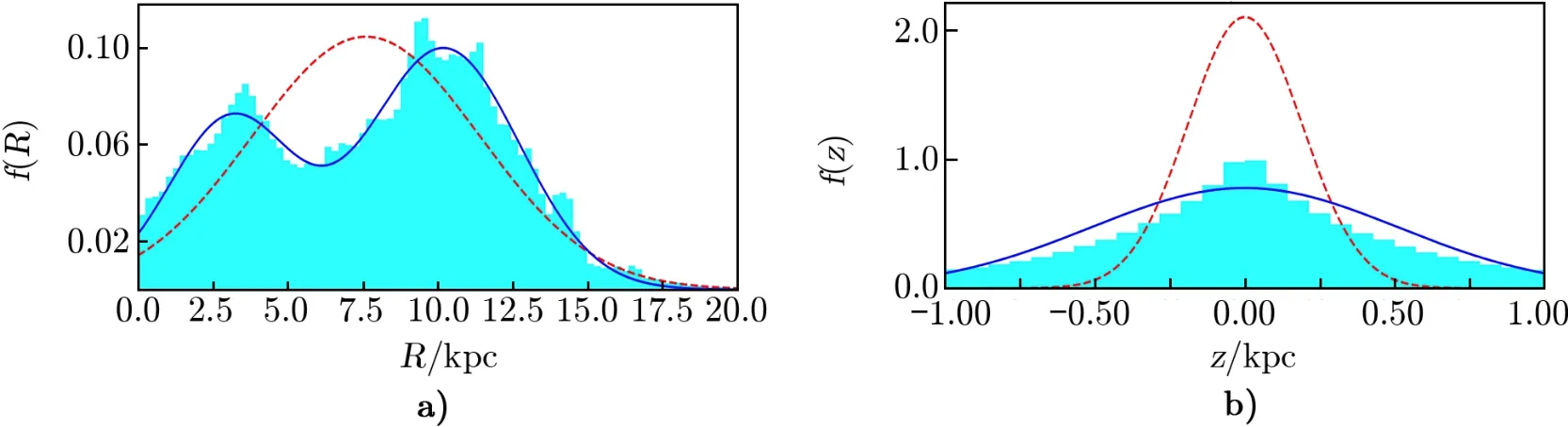
图5 G45 模型中薄盘处新添加的恒星位置的分布图

3.3 薄盘恒星引起的核球质量增长

在G45 模型中，将距离星系中心小于2 kpc 的新恒星作为进入核球区的新恒星，研究薄盘恒星迁移到核球区引起的核球质量变化。如图6 所示，核球区新恒星的质量增长大致可以分为两个阶段：2.4 ～3.0 Ga 的时候，进入核球的新恒星质量大致呈线性增加，说明随着薄盘恒星的形成，这些新恒星不断被棒捕获，变成支持棒的x1 型轨道，进入核球区，迁移往核球区的新恒星数量和总的新恒星数量成正比；而3.0 ～4.8 Ga 时，由于不再添加薄盘恒星，系统质量不再增加，不再有大量恒星从盘上迁移到核球区，因此核球区新恒星质量保持稳定。G45 模型相比于G00 模型(无薄盘)，核球质量在2.4 ～4.8 Ga 阶段增加了4.75×108M⊙，占核球总质量的2%，其中薄盘恒星贡献的核球质量增长仅占19%。这说明核球区的主要质量依然由原初盘恒星贡献，薄盘恒星的添加也促进了原初盘恒星的迁移。

4 薄盘恒星形成对核球区的动力学影响

薄盘恒星在添加入模型中以后，其动力学性质会在棒非对称势场的影响下发生变化。我们将薄盘恒星添加的位置以及恒星形成率作为主要的自由参数，以研究其对核球动力学性质的影响。观测上的银河系恒星形成率大约为1 M⊙·a-1，我们一般采用较大的恒星形成率，以得到更显著的核球动力学性质变化。尽管如此，最终看到的核球区动力学性质依然变化不大，说明银河系薄盘恒星的形成一般不会对核球产生显著的影响。

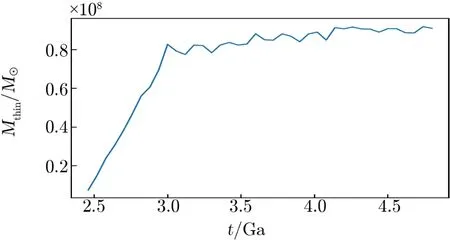
图6 G45 模型中进入核球区的薄盘恒星/新恒星质量随时间的变化

4.1 薄盘恒星对核球区恒星视向速度分布的影响

为了进一步研究这些模型中薄盘恒星对核球动力学性质的影响，我们将模型结果与观测到的视向速度数据进行了比较。图7 是G00, G35, G45, G55 模型结果与观测数据的比较，这些模型的恒星形成率相同，区别在于添加恒星的位置逐渐远离星系中心。以无新恒星添加的G00 模型作为标准对比，可以发现薄盘的形成并不会使得核球区恒星的平均视向速度发生明显变化，但是其视向速度弥散会比无薄盘形成模型的更高；同时，核球区恒星的视向速度弥散与薄盘恒星添加位置有关：添加恒星的位置越靠近棒，对应的核球区恒星视向速度弥散更大。

图7 在不同添加位置时相同恒星形成率的模型结果与观测数据的比较

图8 是G00, G41, G42, G45, G410 模型结果与观测数据的比较，这些模型添加恒星的位置相同，区别在于恒星形成率逐渐增大。而以无新恒星添加的G00 模型作为标准对比。同样发现，薄盘的形成并不会使得核球区恒星的平均视向速度发生明显变化，但是其视向速度弥散会比无薄盘形成模型的更高；同时，核球区恒星的视向速度弥散与薄盘恒星形成率有关：薄盘的恒星形成率越大，对应的核球区恒星视向速度弥散更大。图7 和图8 都可以解释为更多的新恒星迁移到星系中心，使得核球区势场变深，由位力定理得到更大的速度弥散。

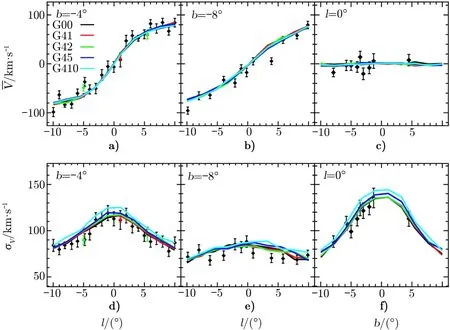
图8 恒星形成率不同时相同添加位置的模型与观测数据的比较

4.2 薄盘恒星对棒的影响

作为星系中最显著的非对称结构，棒对恒星的迁移有着重要的影响。我们研究了薄盘恒星的添加位置对棒的强度以及旋转速度的影响，选择模型中所有距离星系中心0.5 ～2.0 个尺标长度的恒星作为计算棒的样本(尺标长度为1.9 kpc)。棒的强度|A2|由对样本中恒星的方位角进行傅里叶变换的第二项，得到，其中θj是样本恒星的方位角，N 是这些恒星的数量。棒的旋转速度由每个时刻棒的方向变化(A2的相位角)计算得到。当恒星形成率固定，改变恒星添加位置，不同模型的棒强度随时间的变化情况如图9 所示。这些模型中，棒的强度均随着时间波动，呈现出下降的趋势。由于棒和外围旋臂具有不同的旋转速度，两者相互作用会产生类周期性的节拍振荡，导致棒的强度随时间波动。相同时刻下，有薄盘形成的模型比无薄盘形成的模型具有更大的棒强度。棒的强度也与薄盘恒星的添加位置有关：薄盘新恒星添加位置越靠近星系中心，棒的强度越大。当恒星形成率固定时，改变恒星添加位置后不同模型的棒旋转速度如图10 所示：红色虚线代表无薄盘形成的模型G00 的棒旋转速度，图中以G00 作为比较标准；蓝色点为研究的三个具有不同薄盘恒星添加位置的模型对应的棒旋转速度；蓝色实线连接三个模型点，显示了不同薄盘恒星添加位置对棒旋转速度的影响，可以发现薄盘新恒星添加的位置越靠近星系中心，棒的旋转速度越大。薄盘恒星的形成会使星系盘变冷，使其产生“振荡放大”不稳定性，从而出现暂现但可重复被激发的旋臂结构。旋臂的形成会导致更多的薄盘新恒星发生迁移，并与棒交换角动量。而薄盘恒星添加位置越靠近银河系中心，则有更多新恒星被棒捕获，使得对应的棒强度与旋转速度较大。值得一提的是，薄盘形成导致的棒强度与棒旋转速度变化不大，分别不超过30%和5%。

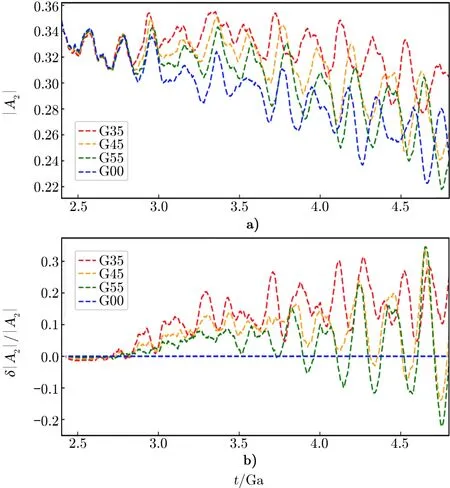
图9 恒星形成率固定时改变恒星添加位置的不同模型的棒强度随时间的变化情况

图10 恒星形成率固定时改变恒星添加位置的不同模型的棒旋转速度随薄盘半径的变化

4.3 薄盘恒星与原初盘恒星的比较

本节我们分析模型G00，G45 中的薄盘恒星(新添加恒星)与原初盘恒星在核球区的视向速度分布。G00 是Shen2010[18]模型在运行了4.8 Ga 的结果，作为比较的标准参照。而G45 在Shen2010[18]的基础上，运行了2.4 Ga 以后，在2.4 ～3.0 Ga 时以8.85 M⊙·a-1的速率在星系薄盘位置添加粒子，而后运行至4.8 Ga 的结果。模型中设置了太阳与银河系中心的距离8.3 kpc，太阳旋转速度220 km·s-1。选取的样本为距离银河系中心不超过4 kpc 作为核球区的恒星。每个视线方向选取的恒星纬度|b|＜1°，经度宽度为2°。

由图11 可知，每个经度处，G45 模型中的原初盘恒星平均视向速度比G00 模型的略微小一点，但相差不大。而与此相反的是，G45 模型中的薄盘恒星平均视向速度比G00 模型中的原初盘恒星的平均视向速度更大。由于原初盘恒星在核球区的质量占主导地位，所以图7 和图8 中核球区恒星平均视向速度基本不变，因为其是略微减小的原初盘恒星视向速度与明显较大的薄盘恒星视向速度经过平均以后的结果。

G45 模型中的原初盘恒星视向速度弥散比G00 模型的略大一点，差异不明显。同时，在经度-5°～5°的范围内G45 的薄盘恒星速度弥散比G45 和G00 的原初盘恒星更小，在动力学上更冷。而在外侧，经度在-20°～-5°，以及5°～20°范围，G45 的新恒星速度弥散比G45 和G00 的原初盘恒星都大，因为在经度较大的地方能看到视向速度较大的沿着棒运动的薄盘恒星，与前景和背景的玫瑰花型轨道恒星视向速度相差较大。

5 视向速度分布

5.1 薄盘恒星和原初盘恒星在核球区的视向速度分布

图11 G00, G45 模型核球区恒星平均视向速度和视向速度弥散的比较

观测上，Nidever 等人[35]在2012 年通过分析APOGEE(The Apache Point Observatory Galactic Evolution Experiment)巡天预观测数据发现，在经度4°～14°，银河系核球区年轻恒星的视向速度分布具有200 ～250 km·s-1的高速峰。Babusiaux 等人[36]在2014 年也在经度6°～10°处发现了类似的高速峰，并且在经度-6°处发现了视向速度大约为-225 km·s-1的高速峰。Zhou 等人[37]在2017 年利用APOGEE 的正式巡天数据发现，大部分核球区的视向速度分布只存在一个平滑的高速肩膀，仅在两三个孤立的视场中存在较明显的高速峰。2015 年，Aumer 和Sch¨onrich[38]在理论模型计算中得到了与观测类似的视向速度分布，并认为高速峰恒星是棒区的年轻恒星，而非盘恒星。正经度处观测到的高速峰恒星为棒近端远离我们的恒星，而负经度处观测到的高速峰恒星为棒远端靠近我们的恒星。Molloy 等人[39]在2015 年提出，高速峰的主要成分可能为构成棒骨架的2:1 共振轨道恒星以及更高阶的共振轨道恒星。

我们将Shen2010 年[18]模型G00 与模型G45 进行比较，以研究薄盘加入以后核球区恒星的视向速度分布的变化，以及是否可以解释观测到的高速峰现象。图12 展示了G00, G45模型在3.0 Ga 时刻核球区恒星的视向速度分布，此刻正好结束添加新恒星。同时选取了该时刻下距离银河系中心不超过4 kpc 的恒星，以筛选出核球区恒星。黑色线与蓝色线基本重合，说明原初盘恒星的视向速度分布并没有随着薄盘的添加发生变化；因为薄盘总质量相对原初盘较小，缓慢添加的薄盘恒星并没有对势场产生明显的影响。银河系为无碰撞系统，原初盘恒星没有与薄盘恒星发生太多碰撞。红色线是模型G45 薄盘恒星的视向速度分布，在正经度处偏向正值(远离我们)，在负经度处偏向负值(靠近我们)。在薄盘恒星加入不久(加入时间不超过0.6 Ga)，薄盘恒星的视向速度分布没有出现明显的高速峰；这是由于薄盘恒星添加位置离棒比较远，这些恒星尚未被棒捕获，依旧属于盘星。而这些薄盘恒星速度方向与视线方向平行的那部分则会投影得到较大的视向速度，与观测上看到的支持棒的高速峰恒星不同。同时在正经度处，速度约为-50 km·s-1处有突起的峰，存在反向速度的恒星。这些反向恒星速度与视线方向夹角都比较大，因此投影得到的视向速度较小。如图13 所示，反向峰可以解释为太阳-银河系中心连线与棒主轴的夹角引起的投影效应：正经度处视线方向能同时看到棒远端远离我们的恒星(主峰)和棒近端靠近我们的恒星(反向峰)，负经度处视线方向能看到棒近端靠近我们的恒星(主峰)和棒远端远离我们的恒星(反向峰)。视线方向与棒主轴的夹角越小，看到的反向峰恒星越少。2015 年Aumer 和Sch¨onrich[38]仅挑选出年轻的棒区恒星时，也能看到类似的反向峰特征。但是如果对视线方向的所有恒星使用类似APOGEE 巡天观测的选择函数，增加年轻恒星的比重，则其视向速度分布中的反向峰特征因太小而观测不到。这解释了为什么APOGEE 巡天观测中没有看到模型中预言的反向峰。

图12 G00, G45 模型在3.0 Ga 时刻核球区恒星视向速度分布

5.2 薄盘恒星在核球区的视向速度分布随时间的演化

图13 投影效应引起的反向峰恒星示意图

模型G45 在加入薄盘形成的模拟以后，原初盘恒星的动力学性质几乎不发生变化；所以我们将注意力集中在薄盘恒星的动力学演化上，研究后续薄盘恒星在核球区的视向速度分布是否会出现观测上看到的高速峰。如图14 所示，我们给出模型G45 核球区薄盘恒星视向速度分布随时间的演化。这些薄盘恒星在2.4 ～3.0 Ga 阶段时加入，后续不再有薄盘恒星加入。从3.0 Ga, 3.6 Ga, 4.2 Ga, 4.8 Ga 的薄盘恒星视向速度变化上看，其主峰逐渐变宽，逐渐接近原初盘恒星的视向速度分布。在薄盘恒星加入的1 ～2 Ga 之后，我们在经度±3°,±6°,±10°处看到了与APOGEE 巡天观测相似的高速峰；但是在14°处，与Aumer2015[38]模型相似，我们也看不到高速峰。因为在视线方向±3°,±6°,±10°看到的恒星主要为支持棒的恒星，而在视线方向14°看到的恒星主要为盘星。这些盘星的运动方向与视线方向平行，呈现出较大的视向速度。模型中的势场与棒的强度并非完美符合银河系的实际情况，模型中视线方向上看到的棒星比例可能与观测不同。同时模型并没有考虑在距离银河系中心4 kpc 处由分子云形成的高密度环[40]，环上形成年轻的恒星很可能会贡献一部分APOGEE 巡天观测到的K/M 巨星。最后，高速峰恒星的比例也随着时间而变化，在4.2 Ga 时刻最明显。随后高速峰逐渐消失，在4.8 Ga 时刻几乎看不到高速峰。这可能是由于薄盘上的新恒星刚被棒捕获时，更加接近周期性轨道；而这些恒星加热过程中，逐渐偏离了周期性轨道，对应的视向速度分布中高速峰消失，主峰变宽。这个模型间接预言了核球区恒星视向速度分布中的高速峰主要由年轻的棒区恒星贡献。年老恒星的视向速度分布中虽然存在高速恒星(Vlos＞200 km·s-1)，但是并没有明显的高速峰，这与观测上的结果并非完全吻合。2017 年Zhou 等人[37]认为核球区的年轻恒星和年老恒星均有高速特征，但是仅有分立的几个核球区能看到高速峰，如在经度6°, 10°处能看到高速峰，而在经度8°处没有明显的高速峰。我们的模型中6°～10°的经度范围内均能看到高速峰，这可能由于观测上对于恒星年龄的界定存在困难，导致一些误差。同时年老恒星的轨道也可能受到年轻的恒星影响。因此对于高速峰恒星年龄组成以及高速峰的形成机制，仍然需要进一步的研究。

为了比较Aumer2015[38]的模型结果，我们采用了与其相似的薄盘恒星添加方式，并命名为GA5。模型GA5 采用与Aumer2015[38]模型类似的指数盘分布作为薄盘恒星的初始位置分布，初始面密度分布为Σ(Ri) ∝Ri×exp(-Ri/hR)。不同之处在于恒星形成速率和新恒星的添加时间，模型GA5 在2.4 ～3.0 Ga 期间以8.85 M⊙·a-1的恒星形成率添加新恒星。图15 展示了模型GA5 核球区薄盘恒星视向速度分布随时间的演化。模型GA5 也同样在经度±3°, ±6°, ±10°处出现了高速峰，而在14°没有高速峰。不同之处在于高速峰的出现和演化时间不同，这可能是因为不同的薄盘恒星初始位置引起的薄盘恒星被棒捕获的时间不同。

图14 G45 模型在不同时刻核球区恒星视向速度分布

图15 GA5 模型在不同时刻核球区恒星视向速度分布

为了研究高速峰对应恒星的演化过程，我们追踪了4.8 Ga 时刻在视线方向l = 10°(经度范围9° ＜l ＜11°)的高速峰恒星(视向速度在150～250 km·s-1范围内)在3.0～4.8 Ga阶段的轨道。这些恒星根据初始位置的不同，可以大致分为三种类型。第一种是在棒上做x1 型轨道运动的恒星，大约有60%，如图16 所示。这种恒星在相当长的时间处于稳定的轨道，速度并没有非常大，但是因为速度方向基本平行视线方向，看到的投影视向速度较大。第二种是从盘上被棒捕获的恒星，大约有20%，如图17 所示。这种恒星随着迁移过程损失角动量，势能转换为动能，获得了较大的速度；因此尽管与视线方向有较大角度，最终看到的视向速度依旧比较大。第三种恒星在初始时刻到星系中心的距离介于前面两种恒星之间，一开始在棒势场拉格朗日点L4, L5(棒有效势场的两个极大值点)附近运动，大约有20%，如图18 所示。这些恒星的轨道逐渐变扁，势能转换为动能，获得了较大速度，因此投影得到的视向速度也较大。

图16 G45 模型高速峰恒星轨道―x1 型轨道

图17 G45 模型高速峰恒星轨道―迁移轨道

图18 G45 模型高速峰恒星轨道―变扁轨道

5.3 薄盘恒星初始位置对视向速度分布的影响

核球区恒星视向速度分布的高速峰主要由被棒捕获的薄盘恒星组成，因此薄盘上新恒星的添加位置可能对高速峰造成影响。恒星形成率相同的情况下，我们将不同的薄盘恒星添加中心半径模型核球区恒星视向速度分布随着时间的变化进行比较，结果如图19 所示。在经度6°处看到的恒星大部分为棒区恒星，因此选择经度6°来研究不同模型的高速峰变化。黑色实线代表这些模型的原初盘恒星视向速度分布，不随着时间与模型薄盘设置条件变化。薄盘恒星的视向速度随着时间有较明显的变化，在3.0 Ga 以后虽然不再有新的薄盘恒星加入，但是高速恒星的占比有短暂的增加，出现了高速峰。不同初始薄盘恒星添加位置的模型具有不同的高速峰形成时间。G25 模型在棒的两端添加新的薄盘恒星，这些恒星很快被棒捕获，轨道变扁，因此在3.0 Ga 时刻拥有最大的高速恒星占比；而模型G35, G45, G55 的薄盘恒星添加位置逐渐远离星系中心，这些薄盘恒星用更多的时间迁移到棒区，形成x1 型支持棒的轨道，因此高速峰出现的时间逐渐变晚。最后高速峰恒星占比逐渐减小，主峰视向速度分布逐渐变宽，甚至覆盖了高速峰，形状上最终接近原初盘恒星。

6 总 结

我们的模型建立在Shen2010[18]多体数值模拟模型的基础上。模型在经过2.4 Ga 的时间模拟后，星系演化出了比较稳定的盒状核球。通过在盘面上添加新粒子的方法，来模拟银河系薄盘处恒星形成的过程，从而研究这些新恒星对银河系核球区域后续演化的影响。我们发现，随着薄盘上新恒星的逐渐形成，这些新恒星密度分布出现了明显的旋臂结构，而原初盘恒星的密度分布没有明显的旋臂，这说明旋臂结构主要由新形成的恒星组成。这些新形成的恒星会冷却星系盘，使其产生“振荡放大”不稳定性，从而出现暂现但可重复被激发的旋臂结构。随后，我们在对薄盘恒星位置分布的研究中发现，薄盘恒星位置分布由初始的单峰分布逐渐变成了双峰分布，说明薄盘恒星大约一半被棒捕获，损失角动量向棒区迁移；另一半获得角动量，向盘外侧迁移；薄盘恒星添加过程中，进入核球区的薄盘恒星质量大致呈线性增长，随后不再添加薄盘恒星，则核球区的薄盘恒星质量几乎不变，说明此时没有明显的薄盘恒星迁移。核球区的质量增长仅有20%左右由薄盘恒星贡献，剩下的由原初盘恒星贡献，说明薄盘恒星的加入还促进了原初盘恒星的迁移。

图19 不同薄盘恒星初始位置模型在不同时刻的视向速度分布

薄盘形成并没有对核球产生明显的动力学影响，除非恒星形成率特别大或者新形成的恒星特别接近棒。薄盘恒星的加入也没有使核球区恒星平均视向速度发生明显的变化，但是有薄盘形成模型的视向速度弥散比无薄盘形成模型的略大。同时，核球区恒星的视向速度弥散与薄盘恒星的添加位置和薄盘恒星形成率有关。添加恒星的位置越靠近棒或者薄盘上恒星形成率越大，则有更多的恒星被棒捕获，迁移到星系中心，相应的核球区势场变深，对应的核球区恒星视向速度增大；薄盘上恒星初始添加位置越靠近星系中心，或者薄盘恒星形成率越大，都会导致核球区势场变得更深，视向速度弥散更大。同时，棒的强度与旋转速度均随着薄盘上恒星的加入而增大，且薄盘上恒星初始添加位置越靠近棒，棒的强度和旋转速度越大。

核球区的薄盘恒星与原初盘恒星具有不同的动力学性质。在视向速度分布的对比中，我们发现薄盘恒星的平均速度比原初盘恒星更大，视向速度弥散则是中间更小，两侧更大。而有薄盘模型的原初盘恒星的平均视向速度比无薄盘模型的视向速度弥散稍大。在这些模型中，原初盘的恒星质量在核球区均占主导地位。这说明有薄盘模型与无薄盘模型的平均视向速度几乎相同，是由于平均视向速度较大的薄盘新恒星与平均视向速度略小的原初盘恒星平均的结果。

对核球区视向速度分布进行分析后，我们发现添加薄盘的模型与不添加薄盘的模型中的原初盘恒星具有相同的视向速度分布。这是因为薄盘的质量比原初盘的小，势能变化不大；薄盘恒星在无碰撞系统下不会对原初盘恒星的运动造成显著的影响。薄盘的恒星视向速度分布具有较窄的峰，动力学上偏冷。模型中在刚添加完薄盘恒星时没有出现显著的高速峰，但是随着时间的演化，在加入薄盘恒星大约1 ～2 Ga 后，在经度较大处能看到高速恒星占比增大，并出现了高速峰。高速峰恒星可能是由被棒捕获的薄盘恒星组成。随着这些薄盘恒星被加热，其轨道偏离周期性轨道，对应的高速峰消失，而主峰变宽。这些高速峰恒星大致分为三种：最主要的一种为沿着棒运动的恒星，约占60%，其速度几乎与视线方向平行；第二种为从盘迁移到棒区的恒星，约占20%，这些恒星发生了较大的势能变化，获得了较大的速度，因此投影得到的视向速度较大；最后一种恒星在初始时刻的位置介于前二者之间，在棒势场拉格朗日点L4, L5(棒有效势的两个极大值点)附近运动，约占20%，这些恒星的轨道逐渐变扁，接近x1 型轨道。同时，我们在-50 km·s-1附近看到了速度较小的反向视向速度峰，这是由太阳- 星系中心连线与棒主轴不平行造成的投影效应导致的。正经度处能看到棒近端靠近我们的恒星，负经度处能看到棒远端远离我们的恒星。但是反向峰太小，可能很难观测到。最后，不同薄盘恒星添加位置会对高速峰的形成时间造成影响，薄盘恒星添加位置在棒两端时，薄盘恒星很快被棒捕获形成x1 型轨道，呈现出高速峰；薄盘恒星添加位置越远离星系中心，则其需要花更多的时间迁移到棒区，所以形成高速峰的时间越晚。