空中声源激发水下声场的建模研究∗
(91550部队 大连 116023)
1 引言
空中声源激发的水下声场传播问题,是水下飞行器试验声学测量领域的研究重点[1],射线声学是该领域的重要研究工具[2]。射线声学与几何光学相似,其描述方法具有直观性,在一定条件下,射线声学的数学运算也有着简洁明了的特点。声线束所携带的能量即为波传播的声能量[3~4]。射线声学只能应用于声波声强没有发生太大变化的部分,譬如波束的中心部分,且介质声速变化缓慢,在一个波长距离上,声传播方向不能发生很大的改变,即射线声学只适用于弱不均匀介质中[5]。在一个波长距离上的变化量,波长越短、频率越高,射线声学的应用条件越容易得到满足,因而射线声学是波动声学在高频条件下的近似[6]。由于射线理论给出的声场解在高频情况下精度较高,具有物理意义明确、直观等优点,空中声源在高频段的辐射噪声穿越空海界面的物理过程可以采用射线声学进行建模[7~8]。
2 平面波斜入射海水界面的数学建模
如图1所示,空气中密度为ρa,声速为ca;海水密度为ρw,声速为cw,平面波从空气透射到水中,入射角为θi,反射角为θr,折射角为θt,入射波声压为pi,反射波声压为pr,透射波声压为pt,反射波声压pr和透射波声压pt不仅与两边介质的特征阻抗有关,而且与声波的入射角θi有关。
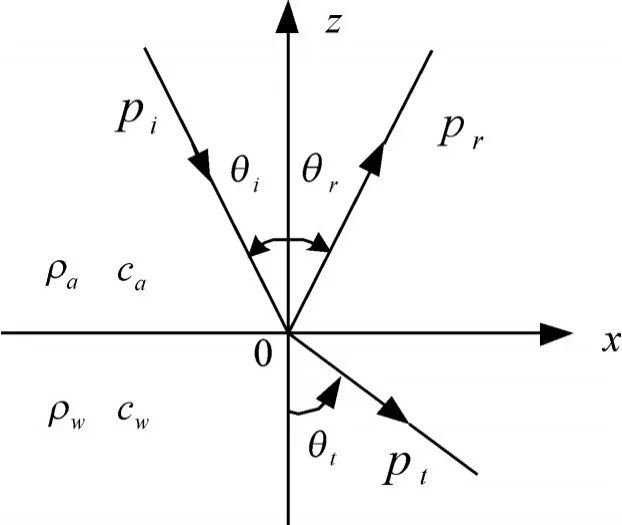
图1 分层介质中的反射和折射
入射波声压为
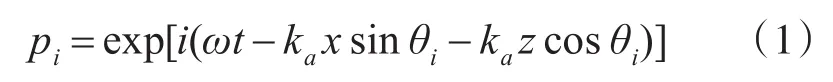
反射波声压为

透射波声压为
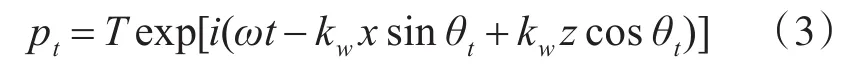
R为声压反射系数,T为声压透射系数。因声压和质点振速的法向分量在空气和海水的分界面处连续,即当z=0时,
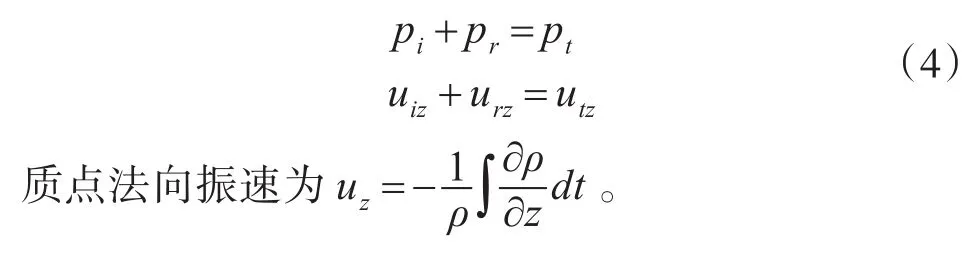
把声压和质点振速代入边界连续条件得到:
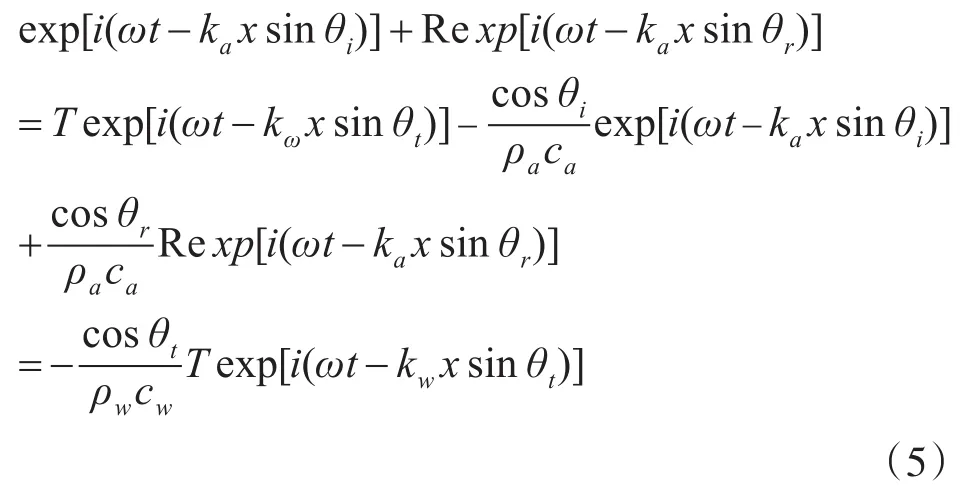
设计仿真条件如下:假设海面处空气密度为1.21kg/m3,声速为 340m/s,海水的密度为1000kg/m3,声速为1500m/s,则图2分别给出了反射系数R模值、透射系数T模值、功率透射系数Tw模值随入射角的变化关系。
3 点声源水下声场射线建模方法
空中点声源辐射球面波,通过空海界面透射入水,当声源与接收水听器和分界面的距离远大于声波波长时,采用射线理论进行声场计算[9]。海水和空气的声波速度差别较大,折射率约为0.22,临界角为13°左右,当入射角小于临界角时,声线可以透射入水,当入射角大于临界角时,声线发生全反射。因此只有在一个小的锥形区域内的声线可以透射入水[10]。
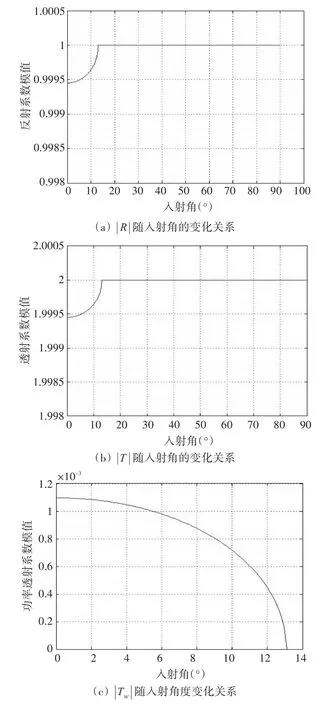
图2 反射系数|R|,透射系数|T|和功率透射系数| Tw|随入射角的变化关系
考虑单位距离处声强为Ia的点源S,位于海平面上方高度h处,如图3所示,假设界面下方任意点R的声强Iw,可以认为Iw和Ia、M、N相关联,

这里M、N分别表示扩展效应、海空界面的投射效应。传播损失10logIw/Ia包含扩展损失-10logM和边界损失-10logN;M、N的表达式为
做一个基本假设:几何声能量不能与声线交叉(即没有散射和衍射),扩展因子M变成只是面积比,称这些区域为dA1和dA2,则

两条夹着场点R的声线沿垂直方向以角度(θ-dθ/2)和 (θ+dθ/2)离开声源,则:
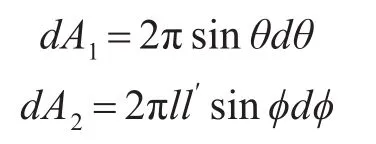
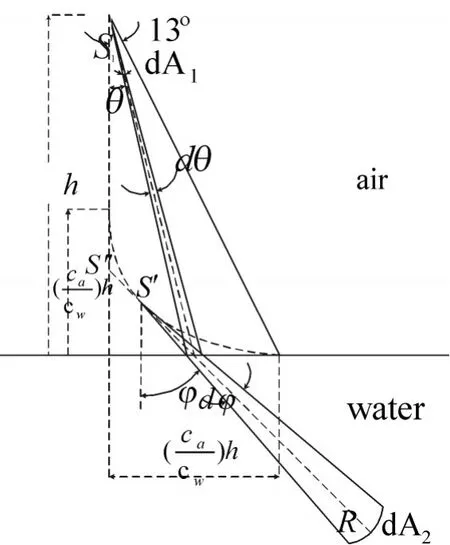
图3 射线声学的几何图
这里l是点S′(两条声线的交点)到R点的距离,l′是点S″(垂直方向上的dA2的旋转中心)到R点的距离,S′是场点R的虚源。虚源的轨迹是一个虚的焦散线,从高于界面(ca/cw)h点扩展到沿界面距离 (ca/cw)h点。距离l和l′在法向声线θ=φ=0时相等,在临界声线θ=sin-1ca/cw、φ=π/2时相差距离(ca/cw)h。当声波通过空气-海面传播时,空气中声速和水中声速之比cacw约等于0.22。
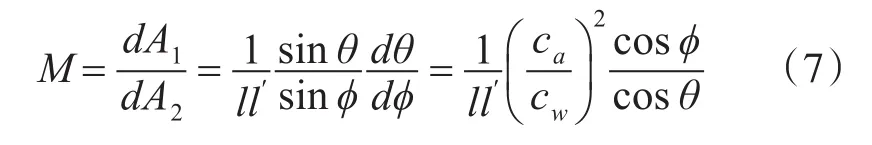
这里,dθ/dφ、sinθ/sinφ可由Snell定理求出,sinθ/ca=sinφ/cw。
对于边界因子N,单位声强入射波的投射波声强为
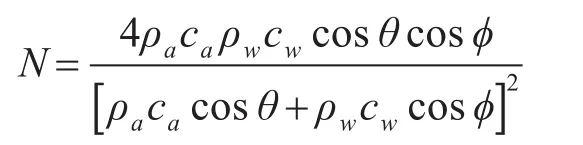
对于空-海界面,ρaca<<ρwcw,分母中的第二项相对于第一项可以忽略不计,得到

将方程(7)(8)代入式(6),得

声强与声压的关系如下:

则:
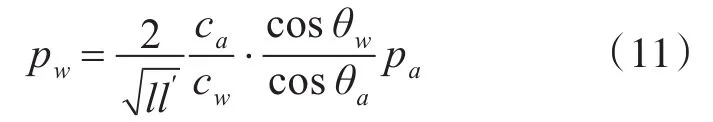
其中,pw为接收点声压,pa为距离声源1m处的声压。
作为一个实际问题,因为水声中使用声压敏感水听器,如果用单位压力下的声强作为两种介质的单位声强,就要去掉比率ρaca/ρwcw。这既是说,使用水中单位压力的平面波声强作为水中的单位声强,空气中单位压力平面波的声强作为空气中的单位声强。还可以去掉cos2θ项,误差小于0.2dB,因为空中声信号在水中传播时θ≤13°,有
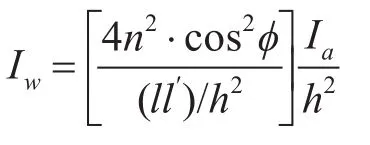
这里Iah2是高度为h的空气中自由场的点源声强。
图4给出了采用该方法的等值线图,归一化为深度dh、归一化距离为R/h,这些等值线是对声强Iah2的修正,图4为水中场点(R/h,d/h)的声强Iw。声源正下方接收声压较大,偏离正下方时幅度较小。
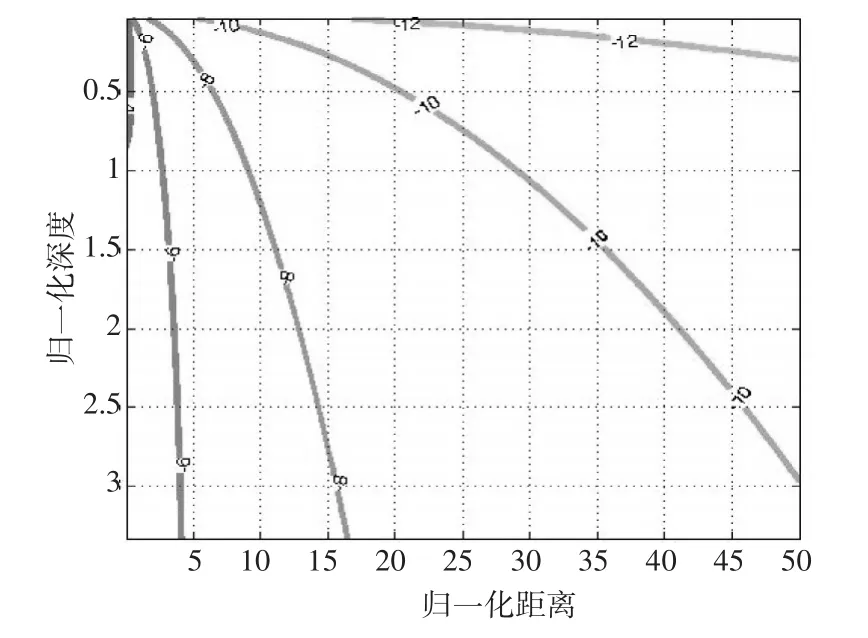
图4 归一化声源高度h的声场等值图
4 点声源的远场声压及正下方声强
1)远场声压
虚源的轨迹可简化为点源正下方界面上的点。从实际的角度出发,在斜距远大于声源高度时出现该情形,即l>>h。在远场l和l′是相同的,可以去掉cos2θ项,误差小于0.2dB,海水和空气的声波速度差别较大,临界角为13°左右,当入射角小于临界角时,声线可以透射入水,当入射角大于临界角时,声线发生全反射。所以:


pw为任意点R处的声压,p为在空气中距声源单位距离处的声压,将上两式代入式(12)得:
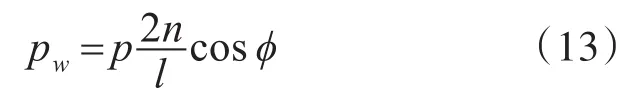
可知:空中点声源在水下产生的声场,在远场声压具有余弦方向性,满足球面衰减规律。
考虑声传播的相位因子,可以得到完整的声压表达式为

2)正下方声强
设d为声源正下方深度的任一点,根据图3有:
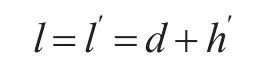
这里h′是虚源高于海-空界面的高度。注意到hdθ=h′dφ,由Snell定理可以得到
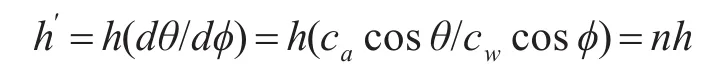
由式(13)得到:
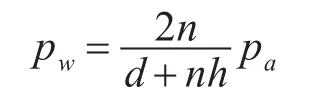
因声源正下方θ=φ=0,当声源正下方的虚源位于界面上方高度为nh时,则虚源的强度是空中点源的2n倍。
5 结语
对空中声源引起的水下声场射线建模方法进行了研究,将空气和海水建模为半无限大空间,讨论了平面波和球面波在空-海界面的透射问题,对空中静止点源水下声场的射线建模结果表明:远场声场具有余弦方向性,满足球面衰减规律,声源下方声波可近似从高度为nh、强度为点源2n倍的虚源发出。

