基于性能的导弹装备购置费用估算∗

高卫刚 陈桂明 孙志鹏 刘汉增 陈 正

（1.火箭军工程大学 西安 710025）（2.海军919167部队航空管制室 邢台 054100）

1 引言

在导弹定价过程中，承制单位为实现经济利益最大化，钻监管和制度漏洞，想方设法抬高导弹装备价格，并设立种种壁垒，这给有关部门价格管理工作造成困难[1]。具体形式表现在三个方面：1）通过增加装备的不必要性能指标来增加成本，抬高价格；2）夸大研发和生产难度，使价格虚高；3）保留新技术或研发不积极，以便留下装备下次升级机会，再获取更多利益。这三方面使装备使用性能与后期维护保养得不到真正保障，其根源在于装备的定价方法始终以成本为基数，使得某些承制单位利用信息不对称钻制度空子，始终把注意力集中在提高装备成本上。这样不仅造成军费浪费，更为可怕的是减缓装备发展速度，影响装备建设效率和效益。

对于新型导弹装备，其研制、生产成本变化原因复杂，如果仅仅采用以往的逐一核查、对账审核的办法来确定装备成本，不仅工作量巨大，而且无法解决由于信息不对称而造成的损失。尤其对于专属零部件或分系统，其成本无法根据市场通用商品的价格进行核对，只能依靠经验，不可避免造成成本虚高[8]。复杂的导弹装备采购审价过程中，只使用简单的核查办法显然是不够的。部队需要购买、获取的是导弹装备作战使用性能，虽然有些部件性能好，可是对导弹作战使用性能没有提高[2]，只会徒增成本，因此，论文研究所涉及的性能，主要是指部队实战所考虑的导弹装备作战使用性能，文中简称性能。所以，要从源头上解决问题，需改变定价思路，调整指导方针，在考虑成本的同时，应以引导承制单位提升装备作战使用性能来增加利益为目标作为价格管理改革的方向，研究出更为科学合理的价格预测方法，从而促进导弹装备研制、生产健康发展。

本文首先结合导弹武器装备结构特点以及性能需求建立完善的指标体系，然后运用模糊贴近度理论通过所建立的指标体系分析计算新型导弹与现役型号的模糊贴近度，通过指数平滑法计算待预测新型导弹购置费用，最后将该方法应用于某新型导弹装备价格预测，以验证模型。

2 性能评价理论研究

2.1 层次分析法

层次分析法（Analytic Hierarchy Process，AHP）是美国运筹学家Satty于20世纪70年代初提出的，是一种将与决策有关的元素分解成目标、准则、方案等层次，在此基础上进行定性、定量分析相结合的多准则决策分析方法[3]。

AHP是一种可用来计算层次权重决策分析方法。其特点是对复杂决策问题本质和影响因素的内在关系进行分析的基础上，采用较少的定量信息便可使决策问题定量化，尤其适用于导弹装备采购价格预测所要依据的性能评价，这种难于直接准确量化的问题。

层次分析法用于性能评价，是将性能评价问题按总体性能、各层次分项性能（元素）直到具体可量化性能指标（元素）的顺序，分解成不同层次结构，然后用判断矩阵特征向量的方式，得出每层次元素对上一层某元素的相对权重，再用加权和的办法求出各底层性能指标元素对总体性能的权重。一般步骤：

1）从问题的性质，即导弹装备整体作战使用性能评价的目标出发，建立性能评价的递阶层次结构。

2）构建底层性能指标元素两两比较判断正互反矩阵，对各指标进行两两对比，排定各评价指标相对优劣顺序，依次建立评价指标判断矩阵。

3）针对某一标准，计算各元素权重。其中，权重计算可采用两种方法，规范列平均法和几何平均法。

（1）规范列平均法即和法。矩阵A每一列归一化得出矩阵B；矩阵B每一行的平均值得出所求权重向量矩阵C。

（2）集合平均法即根法。计算矩阵各行乘积，得出矩阵B；再计算每个元素的n次方根得出矩阵C；将矩阵C进行归一化得出所求权重向量矩阵D。

2.2 模糊贴近度理论

贴近度是用来描述两个模糊集之间接近程度的一种度量方式。

贴近度定义反映了模糊集之间相似的程度，很好地刻划了集合间的相同子集关系和不同子集关系。其关系规则视实际的需要而定，主要有海明贴近度、欧几里得贴近度、黎曼贴近度、几何平均最小贴近度以及最大最小贴近度等。上述不同的贴近度理论应用作用和适用范围各有不同，一般难以比较其优劣，这里采用最大最小贴近度[5]。

2.3 指数平滑理论

指数平滑法是广泛应用于成本估算和价格预测中的一种方法。如将装备视为一模糊集，设已经有导弹装备与新型导弹装备的贴近度为βi，且从大到小排列为有序数列β1,β2,…,βn，相应的成本或价格分别为E1,E2,…,En，按就近原则选择选取贴近度较大的三个已知型号导弹装备的成本或价格为基准，且满足：β1≥β2≥β3，则某新型导弹的装备成本或价格估计值为

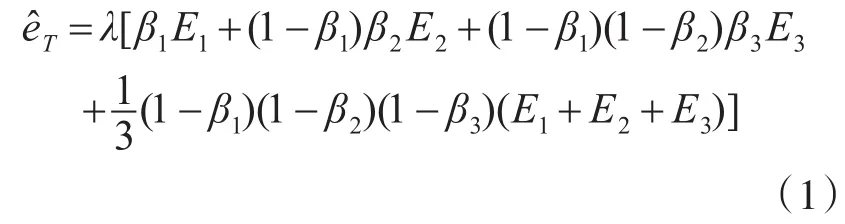
式中，λ是调整系数，主要用于描述选定的三个已知型号装备和新型装备的差异。如果已知型号装备进行成本的估算，其结果将与实际的成本eD相等。即，本文的构造模型就可以保证符合实际，其证明如下：

并假设β1≥β2≥β3，则导弹装备成本估计的值为

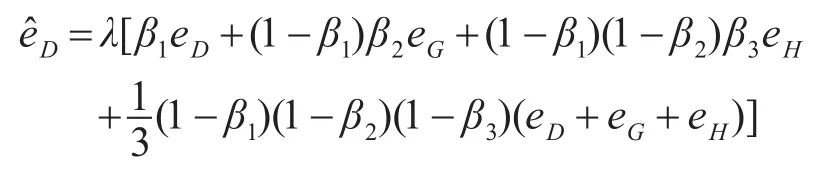
令λ=1，则

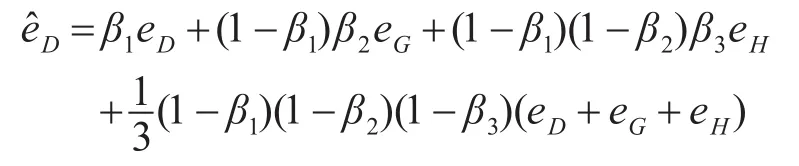
3 费用估算流程

运用模糊数学的综合评价方法建立某新型导弹装备的价格预测模型。在应用模糊贴近度的方法前，建立价格预测模型首先需要筛选影响装备成本的特征因素，并分析性能指标的改进或新型装备与现有装备的相似程度，然后再进行分析计算。

武器导弹装备是一个精密且复杂的系统工程，其性能外延相当宽泛。建立完整且科学的性能指标体系是进行装备性能模糊综合评价的基础，所以需分别对不同的装备性能指标做出评价，然后再确立装备综合指标体系[9]。

3.1 指标体系构建流程

针对导弹装备实际，建立导弹装备性能指标体系。具体流程如图1所示。

1）根据预测对象建立导弹装备性能指标体系

性能指标是评价对象的一种描述方法，首先界定所评价的对象，使评价有的放矢，一般评价对象为装备的作战使用性能。

2）创建导弹装备的性能指标预选集合

（1）分析装备性能，确定装备的内涵和外延，即评价对象分析；

（2）对装备性能进行分解，整理出多个性能参数相关的基本概念；

（3）逐一整理基本概念，并形成描述对象一系列的指标属性。

3）筛选导弹装备的主要性能指标

分解后列出性能指标预选集，通常其较为宽泛，需在保证评价有效、全面的基础上对所有指标进行筛分选择。筛选出重要的“主要”性能指标，将其中贡献较小的指标剔除。在剔除时，可以采用定性、定量分析和专家评定的方法进行筛选。

4）创建导弹装备性能指标体系

根据影响导弹装备性能的主要因子，参考实际预测目标导弹装备数据，通过调研、专家咨询、比较分析、归纳和演绎等众多方法，建立导弹装备性能指标体系。

图1 导弹装备性能指标体系构建流程图

3.2 权重计算

指标权重的确定方法主要有层次分析法、德尔菲法（Delphi）、二项系数加权法、环比评分法等[4]。本节主要使用层次分析法来确定各评价指标与对应上一层指标的相对重要性权值。AHP主要应用于确定性能指标的权重。

1）构造判断矩阵

构造判断矩阵需要对各指标因素两两比较并量化。这种量化的方法一般是给出重要度的标度值，再由专家进行打分判断。该方法的理论依据源自心理学的研究发现，即人们可以区分信息等级的极限能力为7±2种。AHP法采用Satty提出的1-9标度，具体含义如表1所示。

如aij=5，对照表格则i因素比j因素较重要。完成打分结束后可生成相关的正交判断矩阵P。

2）计算单一准则下相对权重

求解判断正交矩阵P的特征根有：

其中，λmax为判断矩阵P的最大特征根，W是相应的特征向量。对W归一化后，即得到同一层次因素相应的权重向量[7]。

3）一致性检验

由于对比评分标准具有一定模糊性，并且专家评分时具有一定的随机性和主观性，因此需对判断矩阵进行一致性检验。其中，用来衡量判断矩阵的不一致程度指标称作一致性指标（CI）。

表1 AHP比较标度表

其中，n为因素的个数。如果CI值越小，则P的一致性则越好。通过引入随机一致性的指标RI，其取值可通过查表2得到。

表2 随机一致性的指数表

如随机一致性比率：

那么判断矩阵P的一致性是否满意，如果不满意则需要重新进行两两比较，并对P进行调整。调整后获得最终权重，即相应层次权重集

3.3 费用计算

本文设定对于某个选定的特征因素，导弹装备的性能越高，隶属度越大。实际上，导弹装备的性能和成本是成正比关系的[11]。

例如，以导弹的射程指标为例，如最大射程为1000km的导弹成本会比500km的导弹成本高，故从射程因素来考虑，前者的隶属度较高。

假设选取m个型号，每个型号有n个特征因素，矩阵即为

其中，xij表示第i个系统的第j个特征因素的数据。

要求最优性能参数，即对每列求最优值，又因负向正向指标转换，则令xj=max(xij)，来代表每列最优值。即第i装备ui关于第j个特征因素yj的隶属度为

对于模糊集合A与B，设：

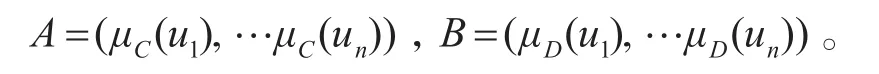
其中，μC(u1)是指模糊集，是相对于性能因素，u1的隶属度。

依据装备审价总结经验，选取最大最小贴近度原则易于实现且最有效[6]，其中，模糊集合贴近度的计算公式为

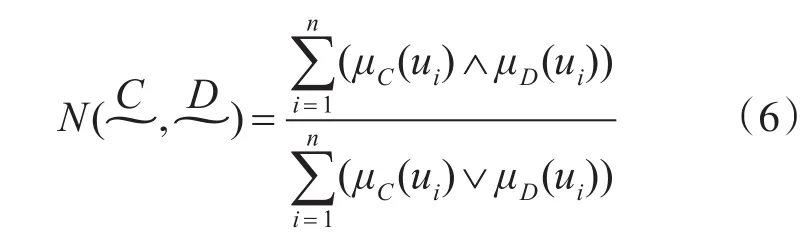
再根据2.3指数平滑理论，将式（6）得出每两个型号的贴近度代入式（1），采用得新型导弹装备价格预测结果。

公式中λ是用来表示所选用的现役型号与新型号间差异的调整系数。若对现役型号成本进行预测，结果与实际成本eD进行比较。

4 实例分析

本文选用一组国外的反舰导弹进行算法可行性的实例验证。选取了1986财年的“World Missile Forecast”导弹成本数据。所有参数和数据均为internet的公开资料，其中选取相同的六组反舰导弹的成本数据作为样本进行模型预测[10]。其中的RBS15导弹是目标进行预测所得结果如表4所示。

将表4的生成特征值矩阵（“成本”一栏数据除外），以式（5）的计算特征因素进行各型号导弹的隶属度计算（通过excel计算，过程不四舍五入），可得隶属度矩阵：

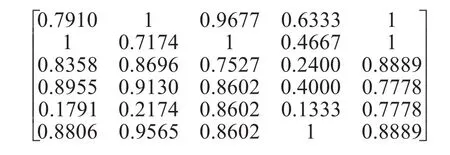
由式（6）算出RBS15导弹与捕鲸叉导弹的模糊贴近度为

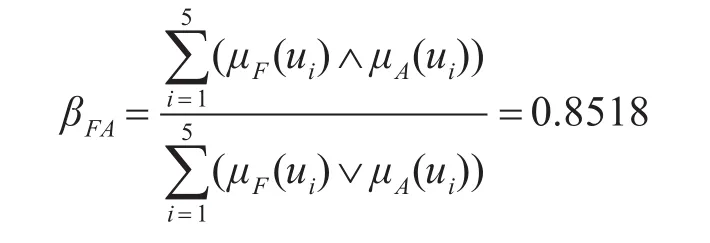
同 理 得 知 ：βFB=0.7695，βFC=0.7821，βFD=0.8328，βFE=0.4727。

则排序有：βFA＞βFD＞βFC＞βFB＞βFE。

令β1=βFA,β2=βFD,β3=βFC,调整系数λ=1，代入式中，可得RBS15的估算成本eˆF=91.0476，与实际值的92相比，其相对误差为1.04%，这就说明估算的结果是可靠的，从而证明了本文提出方法的可行性。

表3 反舰导弹装备相关数据对照表

5 结语

本文研究了基于性能的导弹装备价格预测问题。首先，对抽象的新型导弹装备性能进行了定性分析，建立了相应的评价指标体系。在性能评价模型中，通过定性分析确定评价对象的各项性能指标，并将定性指标较直观地量化，通过模型计算，确定装备性能评价的得分，再利用模糊贴近度理论，建立装备的价格预测模型，并用已知成本或价格的同类导弹装备数据进行了预测与验证。这种方法优点是，可以在不知道各部件成本的基础上对目标导弹装备进行价格预测，并简单易用，能快速预测价格[12]。

基于性能的预测方法缺点是：虽然跳过了成本信息的不对称性，但是由于其筛选出的性能指标是建立在历史数据分析和专家经验基础上得出的权重，使算法本身具有一定的主观性。值得指出的是，由于历史数据准确度会对预测结果的精度产生较大影响，那么如果装备的历史成本虚高，则一定程度上该方法会将此错误延续。另外，如果新研制或改进型的装备采用了新技术、新材料或其他工艺，或武器装备间存在代差，那么装备的成本或进行价格预测时需充分考虑上述因素并进行修正模型。如果特征因素选取越多，或指标选择越详细，那么模型预测的结果精度将越高。