轴承缺陷图像二值化处理及形态学边缘检测∗
(内蒙古科技大学机械工程学院 包头 014010)
1 引言
列车滚子轴承作为铁路列车的关键部件,有关部门十分重视其质量的检测。近些年来,机器视觉和图像处理技术在轴承表面缺陷方面的应用取得了一定的效果,基于机器视觉的检测方法具有检测速度快、识别率高、实时性好、成本较低等优点,对于轴承缺陷图像的二值化处理和边缘检测是该检测系统的重要环节[1],本文对这两方面的技术作出了改进。
目前对于二值化处理的研究大多是通过改进大津法来实现的,效果有了一定的提升,但是时间也有所增加,这无疑会影响检测系统的工作效率[2~4]。本文提出一种快速实用的二值化处理方法,在保证图像分割效果的同时,大大降低了算法运行的时间。
数学形态学方法在近些年开始用于边缘检测,相比于传统的边缘检测算法,经过数学形态学处理后得到的图像有较好的抗噪性和连续性,对于带有椒盐噪声的轴承缺陷图像,本文提出一种抗噪型形态学边缘检测算法,该算法在准确保留边缘特征的同时,也去除了噪声的干扰。
本文研究的四种轴承表面缺陷为麻点、辗皮、擦伤和划伤,其带有椒盐噪声的图像如图1所示。

图1 带有噪声的轴承表面缺陷图像
2 二值化处理
2.1 传统算法
在进行边缘检测前,需要对缺陷图像进行二值化处理。目前,常用的二值化处理方法有自适应阈值法、人工选择阈值法、迭代选择阈值法等。
人工选择阈值法的二值化视觉效果最好,但是需要工作人员的参与,而且要用不同的阈值不断试验来选取最优,比其他两种方法花费时间更多,这会影响视觉检测系统的工作效率;而对于部分缺陷图像,自适应阈值法和迭代选择阈值法并不能很好地分割出缺陷区域,如图2所示,说明这两种算法对轴承缺陷图像并不完全适用。

图2 传统算法的二值化处理
2.2 本文算法
针对这种情况,本文提出了一种根据缺陷图像的灰度均值范围确定阈值的算法,实验证明,该算法既快速又实用。表1是四种缺陷图像的灰度均值和最优阈值的范围。
由表1可以看出,不同缺陷图像的灰度均值范围和最优阈值范围并不相同。本文算法的核心思想是在缺陷图像进行二值化处理之前,首先进行灰度均值的计算,根据不同均值范围,使用不同的阈值对图像进行二值化处理[5],规则如表2所示。

表1 缺陷图像灰度均值及最优阈值

表2 阈值选择规则
使用本文算法进行二值化处理后的图像如图3所示。

图3 本文算法的二值化处理
利用自适应阈值法、迭代选择阈值法分别对四种缺陷图像进行二值化处理,对其运行时间进行比较,结果如表3所示。
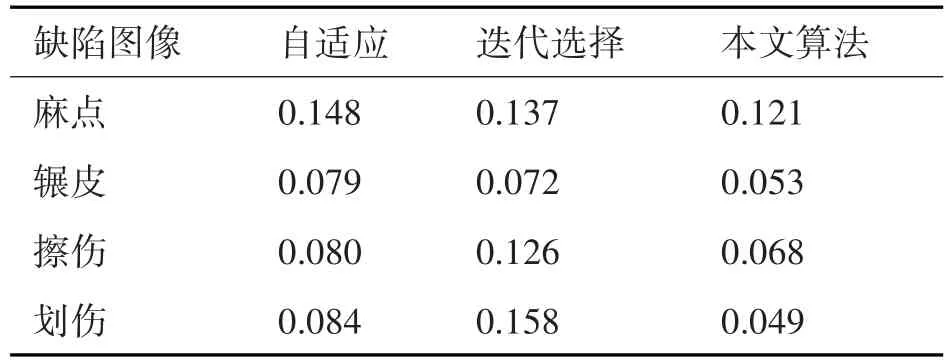
表3 三种算法的运行时间
由表3可以看出,相比于其他两种算法,本文算法运行时间相对较少,证明了本文算法的快速性。
3 形态学边缘检测
3.1 边缘检测算法
数学形态学作为边缘检测中提取图像分量的一种工具,可以根据提取分量的特征,分别采用适当结构和尺寸的结构元素对图像分量进行提取[6]。
对于平面A2上的元素集合B,使用结构元素C对集合B进行形态学处理,得到四种基本运算。
形态学腐蚀:
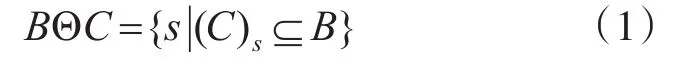
形态学膨胀:
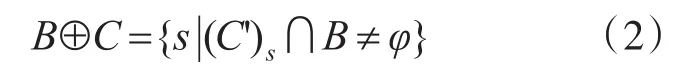
形态学开运算:
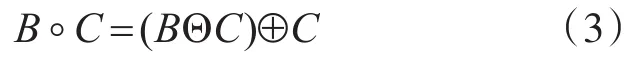
形态学闭运算:

本文提出一种抗噪型形态学边缘检测算法,其数学表达式为
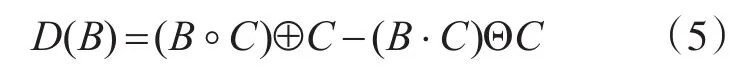
该抗噪型边缘检测算法的原理是开运算后膨胀的图像减去闭运算后腐蚀的图像。因为形态学开运算和腐蚀运算对正向噪声有抑制作用,而形态学闭运算和膨胀运算对负向噪声有抑制作用,所以该算法有抑制噪声的能力[7~8]。
3.2 选取结构元素
对于形态学处理来说,结构元素的选取极其重要,不同结构、不同尺寸的结构元素,对图像的处理效果也有很大的差别。分别对图4中的四种结构元素进行研究,实验表明,结构元素对与其方向平行的边缘敏感性较差,与其方向垂直的边缘敏感性较好;小尺寸的结构元素抑制噪声的能力相对较弱,但是能很好地保留边缘信息;大尺寸的结构元素抑制噪声的能力相对较强,但是难免会破坏边缘信息[9~10]。本文选择3菱形作为本文抗噪型形态学边缘检测算法的结构元素,实验证明,该结构元素的处理效果最好。
4 实验
传统的图像边缘检测处理中,Canny算法是在抑制噪声和准确保留边缘特征之间最好的折中方案[11~12]。但是用于带有椒盐噪声的轴承缺陷图像中,Canny算法的抗噪性明显不足,对图3的四张缺陷图像进行边缘检测,将Canny算法和本文算法进行比较,实验结果如图5~图8所示。
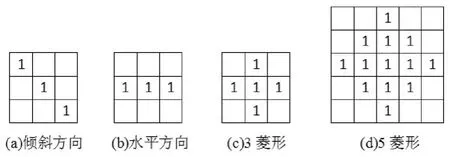
图4 四种不同的结构元素

图5 麻点图像边缘检测

图6 辗皮图像边缘检测

图7 擦伤图像边缘检测

图8 划伤图像边缘检测
本文利用优质系数(FOM)对实验结果进行客观的评价,其数学表达式为
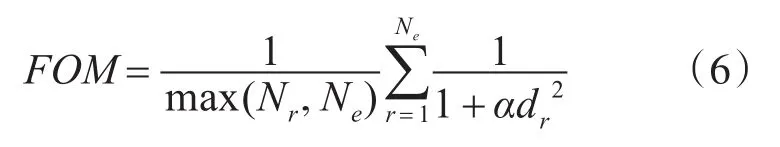
其中,Nr表示图像中实际边缘像素点的数目,Ne表示实验检测到的边缘像素点的数目,α为补偿系数(本文中取为1/9),dr为检测到的边缘点到最近的实际边缘点的距离。由公式的定义可知,FOM取值在0到1之间,其数值越大,代表边缘检测的效果越好[13],对上图求得FOM的结果如表4所示。
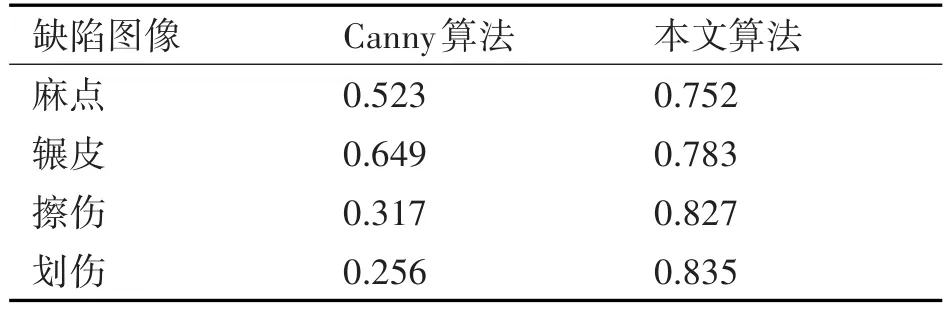
表4 两种算法的FOM比较
由表4可以看出,对于四种轴承表面缺陷的边缘检测,本文算法的FOM比Canny算法要高,这说明本文算法的边缘检测效果相对较好。
5 结语
针对列车滚子轴承视觉检测方法的不足,本文提出了一种二值化处理算法,相比于传统的阈值分割算法,本文算法更加快速实用;提出了一种抗噪型形态学边缘检测算法,对于处理带有椒盐噪声的缺陷图像有明显的效果,比Canny算法的优质系数更高,这证明了本文算法的有效性和可行性。

