基于SCMKF的多观测量联合跟踪滤波方法研究∗

（凯迈（洛阳）电子有限公司 洛阳 471000）

1 引言

滤波是速度跟踪系统的最基本要素，也是估计当前和未来时刻目标运动参数如位置、速度和加速度的必要技术手段[1]。当目标作非机动运动时，采用基本的滤波和预测方法即可很好地跟踪目标。当目标发生机动时，常增益滤波器性能下降，需要通过机动检测改变增益，但这样会使计算量大大增加，失去常增益滤波计算量小的优点。卡尔曼滤波是线性无偏最小方差估计。它具有时变结构，适用于非平稳过程的估计。

因为雷达观测量是在球坐标系中得到，而对目标运动的建模是在笛卡儿坐标系中进行的，所以得到的观测方程是目标状态的非线性函数，这样跟踪滤波问题就成为非线性估计问题。对于非线性估计问题，Li在文献[2]中，总结了三大类方法，即函数近似法、矩近似法和随机模型近似法。其中，常用的扩展卡尔曼滤波（EKF）就属于函数近似法，比较适用于弹载平台数据处理的实时性要求，但EKF是对非线性观测在预测值处做了线性化近似，这种近似带来的误差会比较大，滤波效果也较差。许多学者就提出了改进的算法，本文综合文献[3～5]，给出一种修正的方法，称之为序贯的转换观测卡尔曼滤波（SCMKF）。

2 目标运动模型

在弹载应用中，由于弹目之间的相对机动较大，本文建立了采用非零均值和修正瑞利分布表征机动加速度特性的统计模型[6～7]，与传统的Singer模型相比，它能更为真实地反映目标机动范围和强度的变化。

以（x，y，z）表示目标位置坐标，离散时间的运动模型可表示为

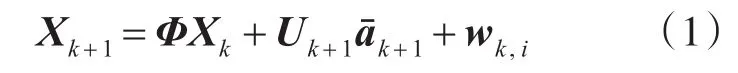
状态转移矩阵：

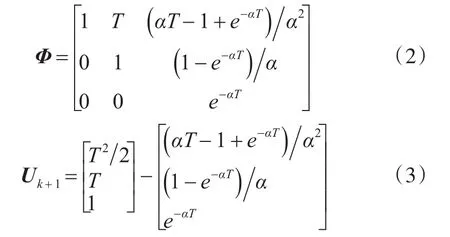
过程噪声：wk～N(0,Qk)。

各变量都要扩展到三维空间中，过程噪声wk,i(i=x,y,z)假设为零均值的高斯白噪声，即wk,i～N(0,Qk,i)(i=x,y,z)。

值得一提的是，此处建立的目标运动模型是在x，y，z三个坐标轴分别建立的，并且假设各坐标轴之间无耦合。

3 主动雷达观测方程

3.1 高重频模式观测方程

主动雷达在不同阶段工作在不同的模式，在弹目距离较远时，主动雷达工作在高重频PD模式，此时能对目标的俯仰角、方位角和多普勒速度进行测量，所以其观测方程可如下建立：

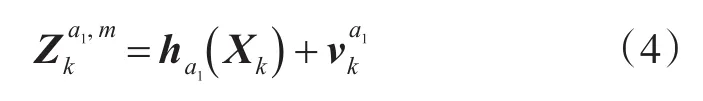
其中：

3.2 中重频模式观测方程

在弹目距离较近时，主动雷达切换到中重频PD模式[9～10]，增加了对目标距离的测量，所以此时观测方程可如下建立：

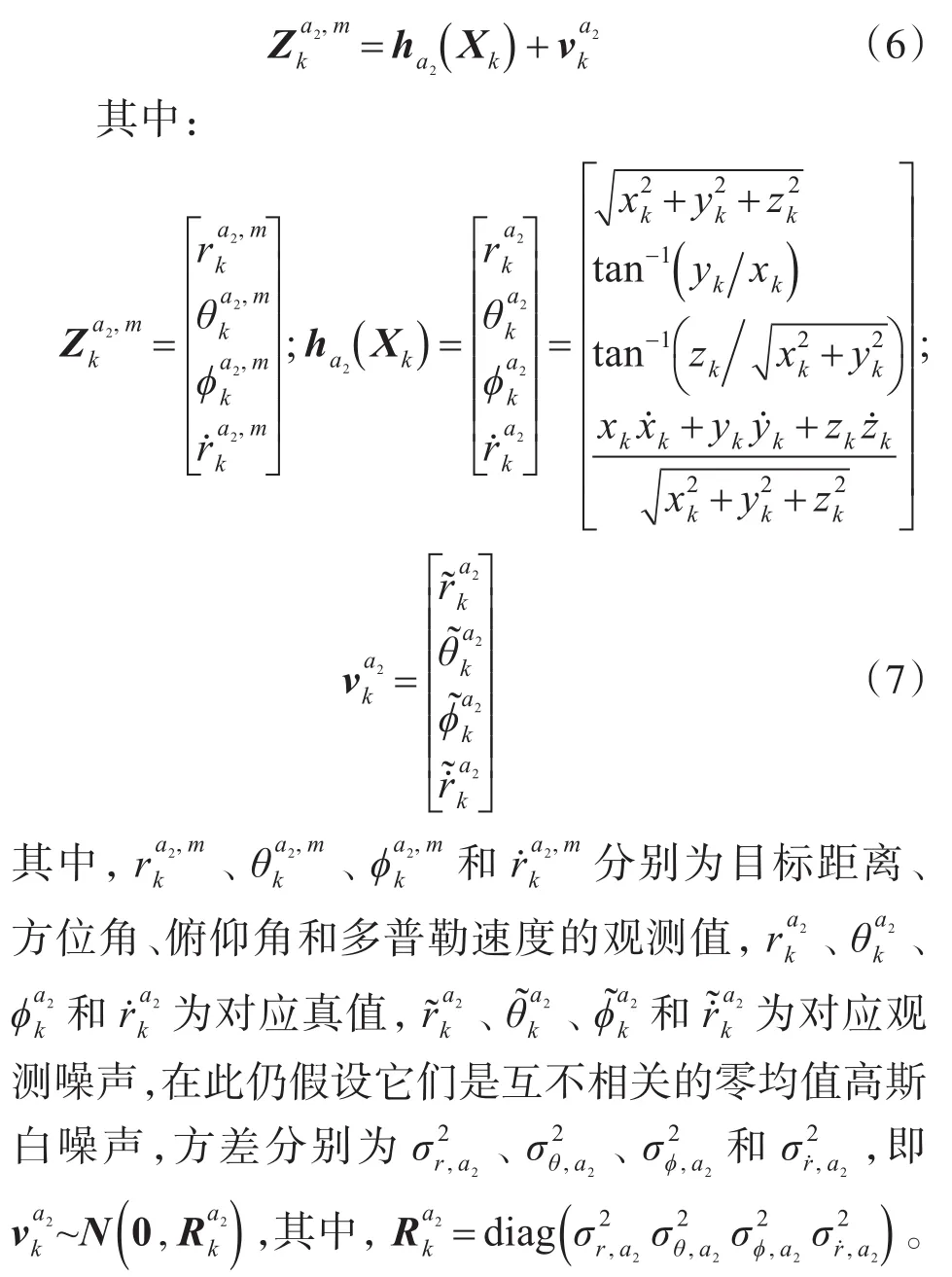
4 基于SCMKF的滤波算法

在中重频模式下，主动雷达不仅可以对目标角度进行测量，还可以测量目标距离，这样就可以利用观测转换的方法，将球坐标系下的观测量转换到笛卡尔坐标系下，从而与目标状态呈线性关系，可以利用标准卡尔曼滤波算法[11]。而对于多普勒观测量，仍然与目标状态是非线性的，这里采用文献[12～13]中的方法，认为位置滤波结果足够精确，可以对多普勒观测量进行线性化。

4.1 位置观测转换

将球坐标系下位置观测转换到笛卡尔坐标系下，得到线性形式的位置观测方程[14]：

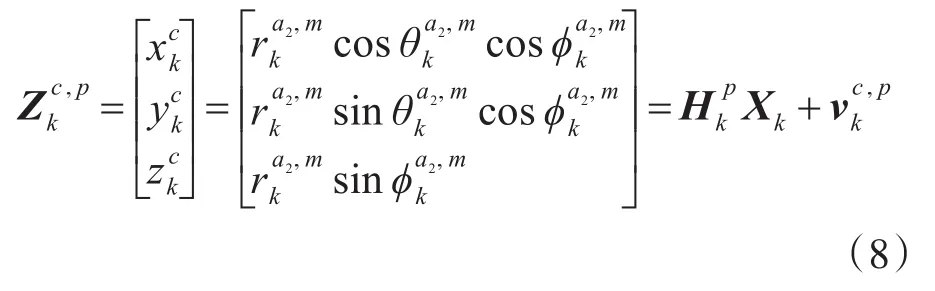
转换的位置观测噪声：

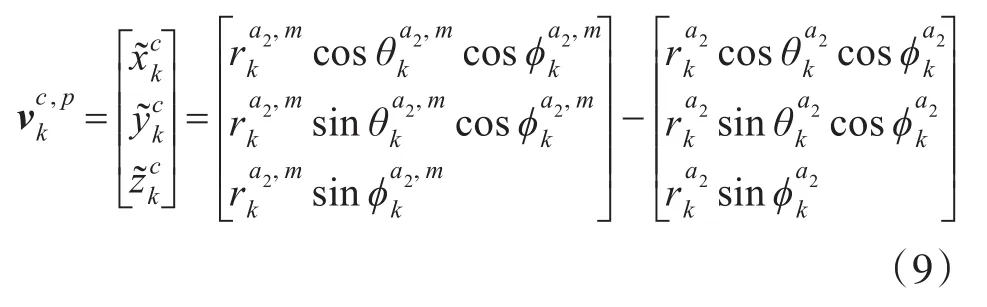
进行近似得到非线性观测方程（8）的Jacobi矩阵为

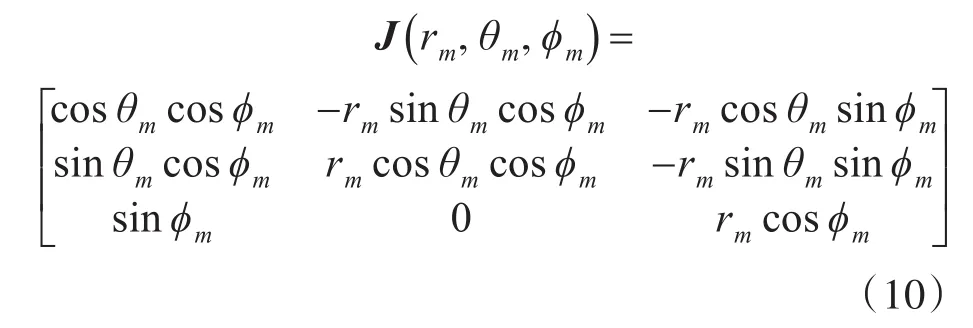
4.2 多普勒观测的线性化

由于多普勒观测量与目标状态呈非线性关系，对其做一定的数学变换，变为速度状态变量的线性形式，如下：

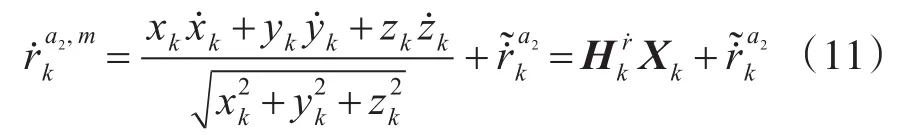
实际中，目标位置未知，观测矩阵中Λk分量也无法知道，但在后续滤波过程由于采用序贯的滤波方法，观测矩阵可以近似计算。

4.3 SCMKF滤波算法

通过上面的处理步骤，转换的观测量都变成了目标状态的线性表示，标准的卡尔曼滤波算法可以直接应用。值得一提的是，这里采用序贯的处理方法，先对转换的位置观测量进行滤波，再对多普勒观测量进行处理，其中多普勒观测量的观测矩阵中目标状态值可以用位置观测滤波后结果带入计算。

这样目标运动模型式（1），位置观测模型式（8），多普勒观测模型式（11），构成系统模型，具体序贯的滤波算法步骤如下。

Step1：时间更新滤波估计

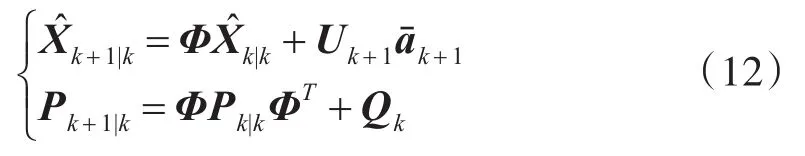
Step2：位置观测更新滤波估计

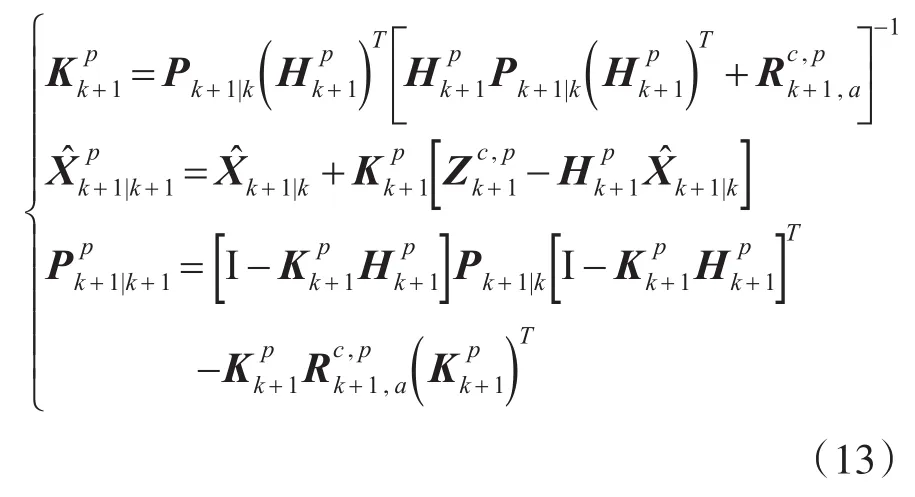
Step3：多普勒观测更新滤波估计

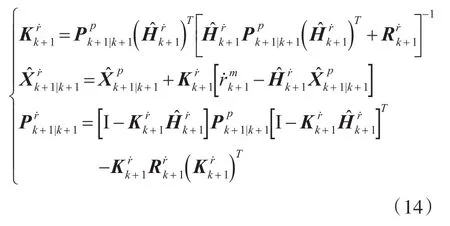
Step4：最终滤波估计

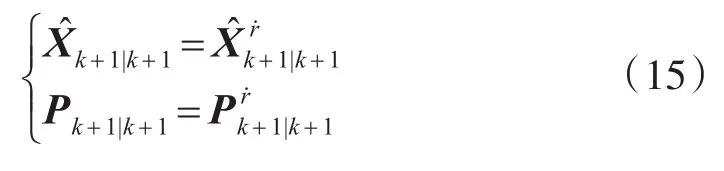
5 仿真验证

仿真场景设定如下：

距离观测噪声：σr=30m；

方位角观测噪声：σθ=0.2°；

俯仰角观测噪声：σφ=0.2°；

多普勒速度观测噪声：σṙ=2m/s。

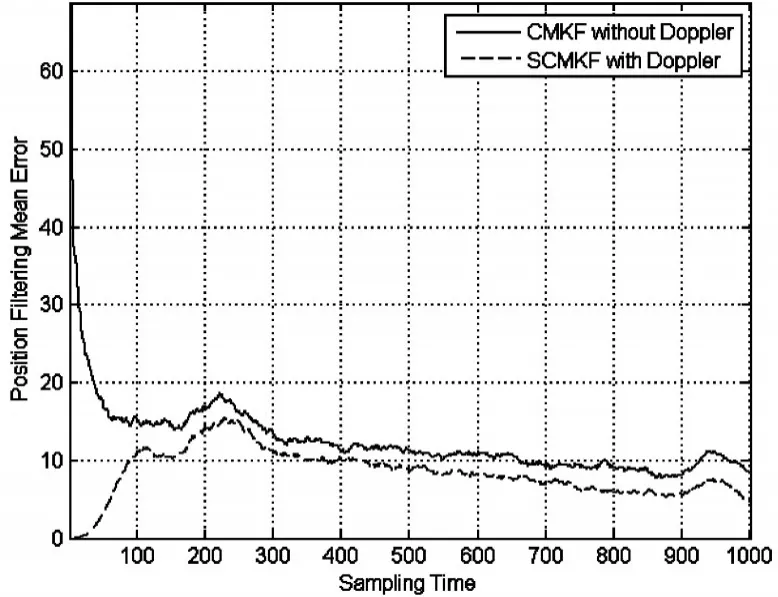
图1 位置滤波平均误差

Monte Carlo仿真试验次数为200次，图1、图2和图3分别给出了滤波误差的统计情况。由图可以看出增加多普勒观测后，无论是位置、速度，还是加速度，滤波误差明显减小，可见SCMKF方法的有效性。周宏仁在文献[6]中指出，增加多普勒观测量，观测矩阵的秩提高了，可以提高跟踪精度。实际上，引入多普勒观测，相当于在位置、速度和加速度的传递函数中增加了一个零点，因此，跟踪滤波器的带宽增大了，动态误差自然减小了。

图2 速度滤波平均误差

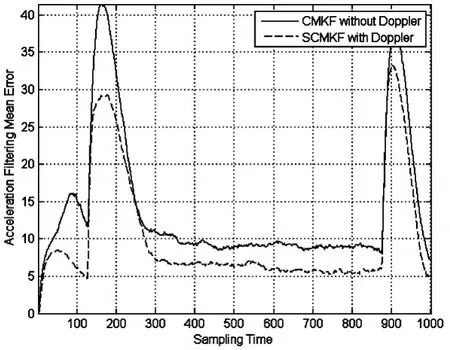
图3 加速度滤波平均误差

6 结语

本方案通过增加多普勒观测拓展了跟踪滤波器的带宽，通过线性化处理简化了计算方法，提高了跟踪精度，仿真结果验证了该方案的有效性。基于本设计思想开发的滤波算法已在某主被动雷达信息处理系统中应用，具有跟踪精度高、可靠性好的优点。