基于ECEF的双阶扩展卡尔曼滤波误差配准方法∗

（海军航空大学 烟台 264001）

1 引言

随着航空发动机技术与新型隐身涂料的发展，高机动性、隐身性已经逐渐成为当前新型战斗机发展的主流。单一雷达已难以实现对目标的精准探测与跟踪。多雷达组网技术通过对多部部署雷达探测到的航迹进行融合[1]，能够有效获取精准的目标行动轨迹，判别目标的作战意图。但是，组网雷达性能的优劣显著受制于装备误差的大小，尤其是系统误差的存在对雷达效能的发挥产生极大影响。因此，在实施多雷达组网行动中，必须考虑对雷达装备的系统误差进行估计与配准。

多雷达组网误差配准算法根据数据处理时机的不同分为两种主要方式，即静态处理方式与实时处理方式。其中，静态处理方式[2～3]是在已获取多雷达探测数据后，利用静态数据处理算法对系统偏差进行融合估计。实时处理方式[4～5]能够在目标跟踪过程中持续对系统偏差进行估计与修正，且修正的精度随着观测值的获取不断提升。扩维系统误差配准方法[6]即是一种效果较好的系统误差实时修正方法，其将系统误差向量与状态向量进行组合，利用卡尔曼滤波技术进行状态与系统误差的同步估计，但组合向量维度增加，尤其是系统误差参数较多时，会严重降低算法的计算效率[7]。另外，在多雷达配准中，为对一目标实施可靠的全局性的态势监测，需将单一传感器的量测数据转换至同一公共坐标系中进行处理，而地理坐标转换法[8]是一种高精度的坐标转换方法，其以地心地固坐标系（Earth centered earth fixed coordinate）为公共坐标系。目前，基于ECEF坐标系的传感器配准研究在批处理方法[9～10]与实时处理[11～13]上均得到良好应用。

为有效解决扩维误差配准算法因维数增加导致的计算量增大，并且消除立体投影引入的量测误差，本文在基于ECEF坐标系下提出了一种双阶扩展卡尔曼滤波误差配准方法。

2 坐标转换

设定组网雷达系统包含两处3坐标雷达平台，各平台观测值描述基于平台自身本地坐标系，固定雷达平台位置事先由高精度导航设备组成，基于地理坐标系进行位置描述。以地心地固坐标系作为不同坐标系之间坐标转换的标准，以雷达1本地坐标系作为数据处理中心建立配准模型，利用系统误差配准方法实时估计修正雷达系统误差。相应的坐标转换公式如下：

假设雷达在本地雷达坐标系下的量测为(γ,θ,η)，其中：γ为径向距离，θ为方位角，η为俯仰角。在直角坐标系下的量测为(xl,yl,zl)，则雷达对目标的测量值在直角坐标系下表示为

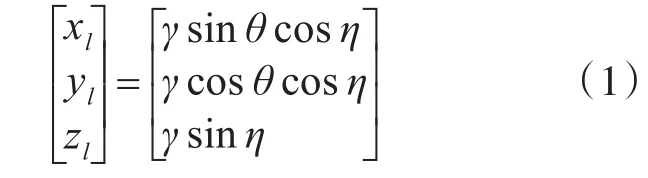
在大地坐标系下，雷达在地球的地理位置可用(L,λ,H)表示。其中：L，λ分别为雷达的大地纬度和经度，H为海拔高度。雷达基于地心地固坐标系的位置坐标描述为(xe,ye,ze)，则雷达于地心地固坐标系与地理坐标系之间的坐标转换公式为

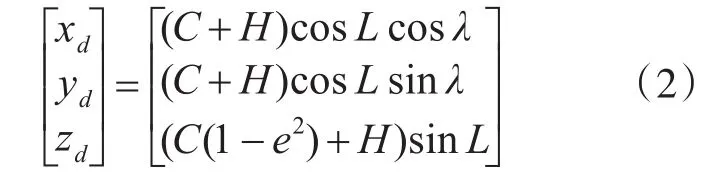
假定目标在ECEF坐标系下的位置坐标为(xe,ye,ze)，则经过旋转平移可实现目标由本地雷达坐标系到ECEF坐标系下的关系转换即：

其中(xe,ye,ze)由式（2）所得，ψ为正交变换矩阵，为

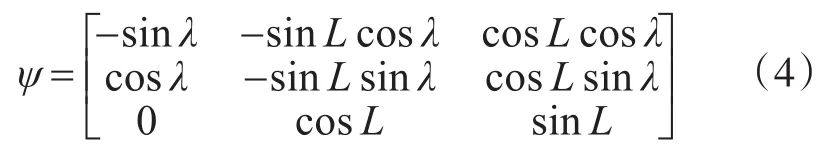
3 滤波模型建立

以地心地固坐标系为参考系，确立雷达1为进行配准的处理中心，建立固定平台的多传感器配准模型。假定目标为匀速直线运动，其状态方程为Xk=Fk-1Xk-1+Wk-1，式中，目标状态Xk定义为，状态转移矩阵定义为

式中，T为时间间隔。Wk-1为零均值高斯白噪声，对应的协方差矩阵为Qk-1。假定，(Li,λi,Hi)(i=1,2)分别为两部三维雷达平台的地理坐标，由式（2）得到与其对应的地心地固坐标为。k时刻传感器的量测为，系统偏差为，这里假定系统偏差是时不变的。为零均值高斯白噪声，其对应的噪声协方差矩阵表示为。由直角坐标系与极坐标系之间的转换方法，将雷达本地极坐标系下的目标量测转换为直角坐标系表示

根据雷达本地直角坐标系与ECEF坐标系间的转换，将传感器i的本地直角坐标系转换到ECEF坐标系中，有：

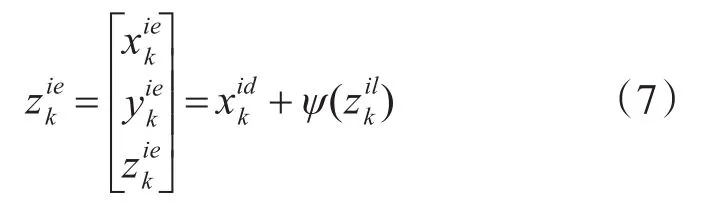
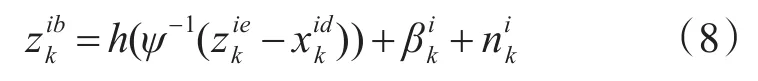
其中：

设定雷达1为联合数据处理中心，首先将雷达2的量测转换到ECEF坐标系中，在利用ECEF坐标系与本地坐标系的坐标转换关系，将雷达2 ECEF坐标最终转换到以雷达1为中心的联合数据处理直角坐标系中，则

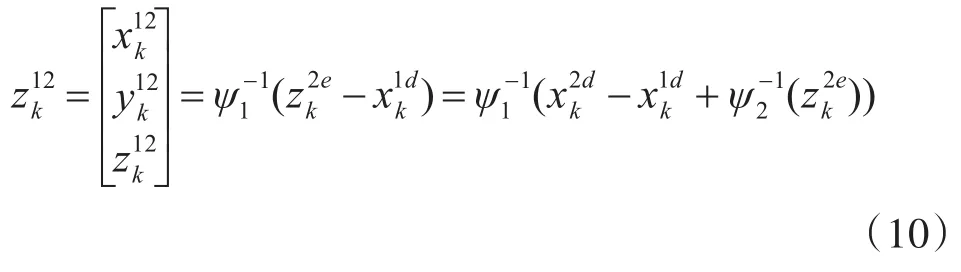
4 双阶扩展卡尔曼滤波误差配准方法

扩维误差配准算法中，系统误差向量作为未知向量并入到目标状态向量中，即组成新的扩维向量其中为目标运动向量，b=[Δr1Δθ1Δη1Δr2Δθ2Δη2]′为两部雷达的系统偏差向量。为了实现扩维滤波，定义如下量测方程和状态方程：

建立目标状态状态方程与量测方程后，即可利用扩展卡尔曼滤波方法实现目标向量与系统误差向量的实时联合估计。但所提出的扩维算法中，扩维滤波使状态向量维数增加，相应的计算效率也随之下降。为了提升计算效率，本文在ECEF坐标系下，结合Freidland[14]提出的双阶卡尔曼滤波思想与传统的扩展卡尔曼滤波思想，将其应用到误差配准上，提出了一种基于ECEF双阶扩展卡尔曼滤波误差配准算法。

对扩维向量解耦为目标状态向量与系统误差向量，相应的动态模型为

其中，Q(k)为零均值高斯白噪声对应的协方差矩阵，并假定雷达的系统偏差为时不变的。

量测方程为

双阶卡尔曼滤波将扩维滤波分解为两个并行滤波，第一个滤波是忽略偏差滤波，第二个滤波是偏差滤波，其滤波结构如图1所示。

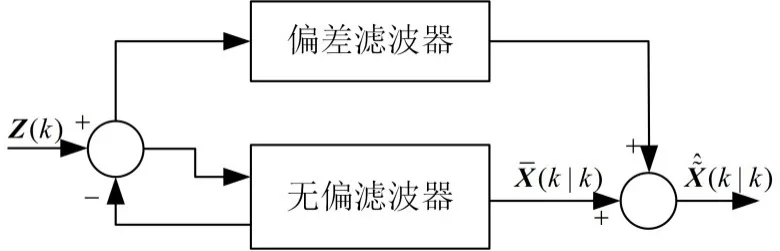
图1 双阶扩展卡尔曼滤波器结构

4.1 忽略系统误差滤波

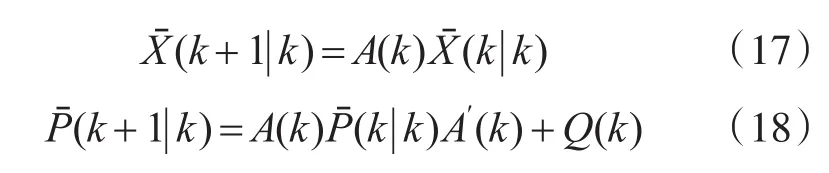
新息协方差为

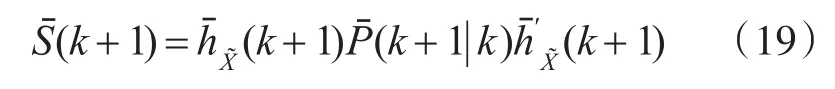
无偏差滤波器滤波器的系统增益为

状态向量更新及状态协方差矩阵更新为

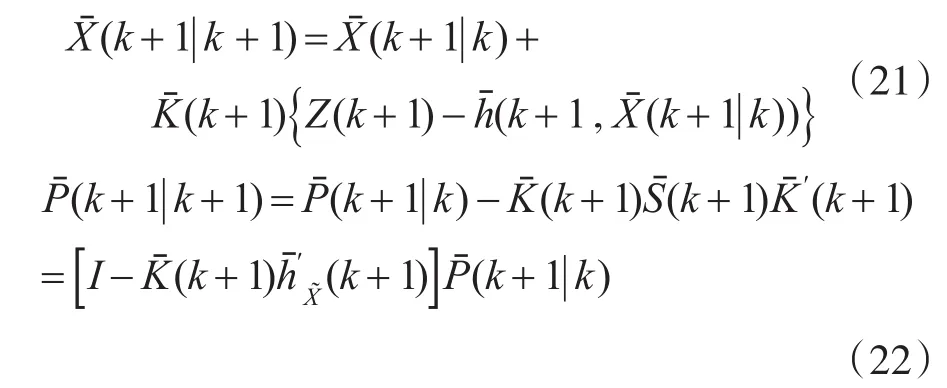
其中

4.2 系统误差滤波

设定b(k)为系统偏差的估计值，利用文献[14～15]给出的结果，设计系统偏差滤波器。

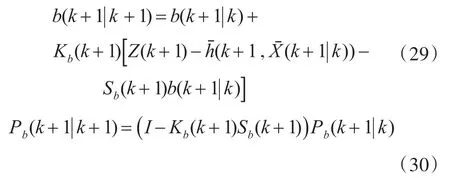
其中

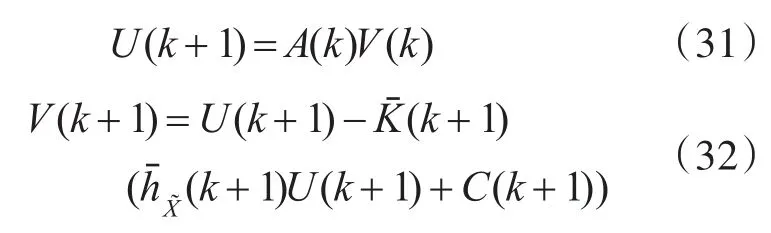
式中I与C(k)均为6维单位矩阵。

4.3 融合后滤波

分别对状态向量与系统误差向量进行滤波后，对其滤波进行融合，即可得到与传统的扩维滤波算法相同的效果。其中，目标状态估计及其协方差矩阵为

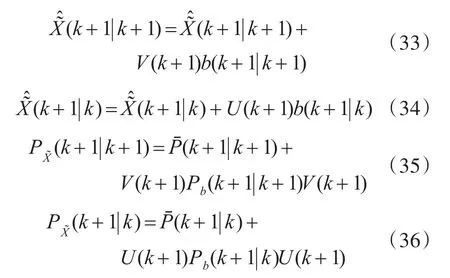
4.4 滤波初始化

利用两部雷达前两个时刻的量测数据对忽略系统误差滤波进行初始化，本文利用雷达1的量测值来初始化目标初始运动状态，为

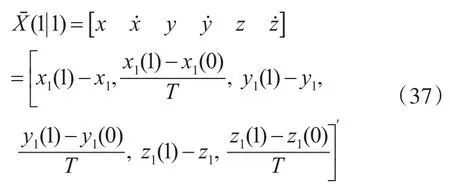
式中(x1,y1,z1)为雷达A的坐标，T为探测周期。

初始协方差矩阵为

式中

在缺少先验信息条件下，设定系统误差向量为

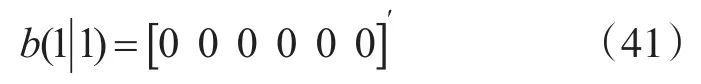
其初始协方差矩阵为

式中Δrmax，Δθmax为系统偏差可能的最大值，knum为放大系数。设定V的初始矩阵为

5 实验仿真

为验证本文算法有效性，进行仿真实验如下。选择地球测地系统于1984年参考的椭圆为地球模型(Eq=3443.9km,e2=0.006694)，假设两部雷达的初始地理坐标分别为雷达1(68.923°,-137.2589°,50m)，雷达 2(70.1714°,-124.725°,218m)。雷达 1和雷达2的量测精度均为er1=er2=100m，eθ1=eθ2=1°，eη1=eη2=1°。两部雷达的系统偏差分别为 Δr1=2000m,Δθ1=0.0087rad, Δη1=0.0175rad,Δr2=1500m,Δθ2=0.0047rad, Δη2=0.0175rad 。以雷达1的本地直角坐标系生成用于配准的航迹，为

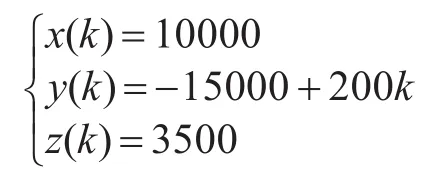
图2 x轴方向目标状态估计效果

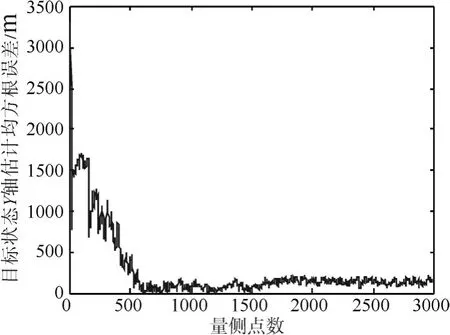
图3 y轴方向目标状态估计效果

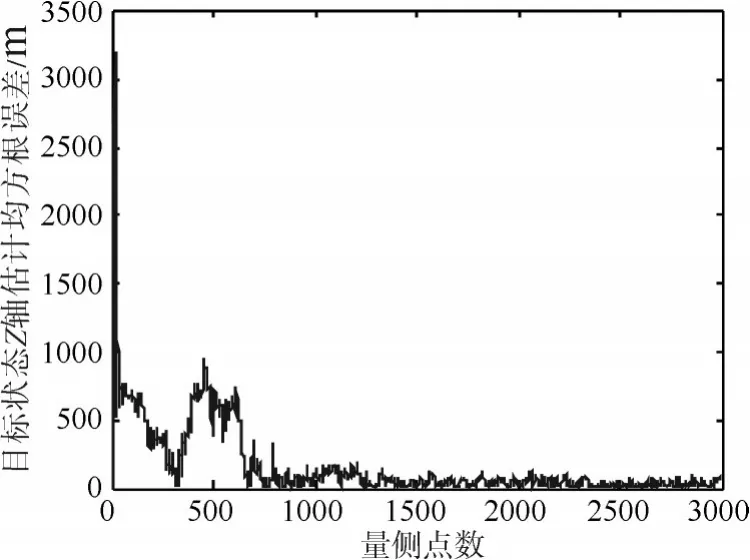
图4 z轴方向目标状态估计效果

迭代步数为3000。雷达1作为数据处理中心，图2、图3、图4分别给出了x、y、z轴的目标状态估计均方根误差RMSE的曲线变化趋势，明显看出系统误差随着本文所提算法的收敛得到修正。

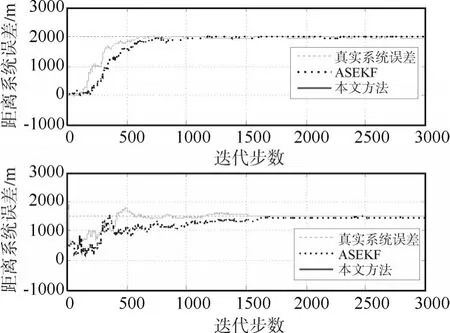
图5 两部雷达系统径向距离偏差估计效果

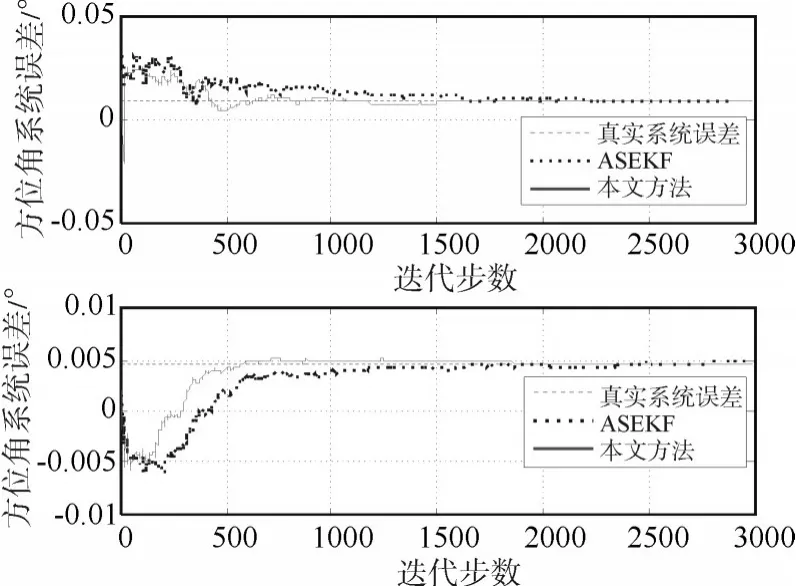
图6 两部雷达系统方位角偏差估计效果

图5、图6、图7分别给出了两部雷达系统分别采用扩维算法以及本文所提算法对径向距离偏差、方位角偏差以及俯仰角偏差的估计效果，表1为两种方法收敛时间对比。数据表示，本文所提算法的计算效率相对于传统扩维算法明显提高。

图7 两部雷达系统俯仰角偏差估计效果

表1 滤波收敛时间对比

6 结语

本文以一个传感器为数据处理中心，以地心地固（ECEF）坐标转换为基准建立配准模型，对组网雷达系统误差实时配准问题进行了研究。在对传统扩维误差实时配准算法的计算效率问题进行研究后，结合双阶解耦思想，提出一种基于地心地固坐标转换的双阶扩展卡尔曼滤波误差配准方法。通过仿真结果表明，新算法有效解决了传统扩维算法计算量大的问题，且消除了立体投影引入的量测误差影响。