问题激活思维 思考提升素养
刘宇
数学课堂,是有思维的课堂。复习课,是整合知识、构建体系的最重要的课型,是培养学生思维的重要契机。学生在问题的驱动下,激活思维,主动思考,从而培养思维的批判性、逻辑性,提升核心素养。
初一学生仍然处于由具体思维向抽象思维过渡的阶段,本章的复习,更要把重点放在思维的培养上。在一元一次方程的复习课中,如何借助问题,发展学生的思维能力?
一是通过变式问题,使学生对概念的理解更全面、更准确。
反向思考,可以提升学生对知识的运用能力和举一反三能力,体现思维的完整性、逻辑性、理据性。
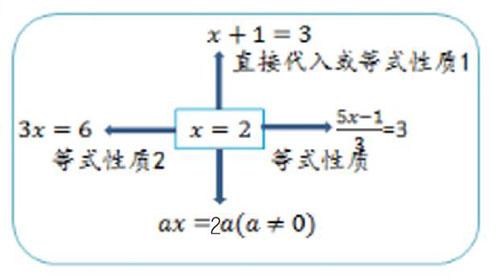
问题1:请写出一元一次方程,并理解每一步变形的依据。问题2:若方程的解是x=2,你还能否写出一个与它同解的一元一次方程吗?追问:能否说出你是怎样构造的呢?依据是什么?
问题1是顺向使用等式的性质理解解方程的一般步骤,问题2则是通过构造同解方程,逆向应用等式性质。构造同解方程时,“两边乘以谁都可以吗”?学生的质疑引发了对等式基本性质的准确理解。交流后发现,对于ax=2a,要加上a≠0的条件,才能构造同解方程。
问题3:你如何理解方程x-3=4+m?它的解有可能是2吗?
在这个问题中,学生需要解决两个问题,一是要理解字母的意义,二是要确定未知数。如果是关于x的方程,它的解可以是2吗?交流后发现,方程的解x=m+7受m值影响,从而解决了字母和方程的解两个难点。
二是通过开放问题,鼓励学生提出新问题,提升思维能力。
由“方程的解”引发出一类数学问题,字母的干扰大大增加了问题的难度。怎样让学生突破这个难点?开放性的问题,可以以点带面,将碎片化的数学题变成数学问题,系统地构建起数学知识和方法的思维体系。
问题4:关于x的方程x-3=4+m的解 (此处开放问题),求m的值(或与m有关的代数式的值)。
学生需要明确方程的解与字母的关系,初步感知函数关系。开放型问题的意图就在于让学生真正理解方程的解与字母系数的关系。
如此一来,学生能够将方程的解与其他知识建立联系,也就形成了自己的知识体系和方法,优化了问题之间的逻辑关系,从而提升了数学的学科能力和素养。
用问题激活学生的思维,要抓住主要知识和主要思想,帮助学生将碎片化的知识和问题梳理成有逻辑关系的知识体系,设置问题链、问题串、问题网,优化思维梯度,促使学生更好地理解与运用,从而提升学生的数学核心素養。

