基于循环平稳周期延拓EMD的滚动轴承故障诊断研究

刘佳杭 王伟韬 刘振涛 何振鹏

摘 要：經验模态分解可根据信号本身变化进行信号分解，具有较好的自适应和时频分辨能力，应用较为广泛[1-3]，但存在端点效应和模态混叠问题。此外，旋转器械（轴承，转子系统等）具有对称结构，其正常和故障信号都具有循环平稳性，本文提出基于循环平稳周期延拓的EMD改进方法，并进行滚动轴承故障诊断，取得了较好的效果。

关键词：经验模态分解;改进方法;滚动轴承;故障诊断

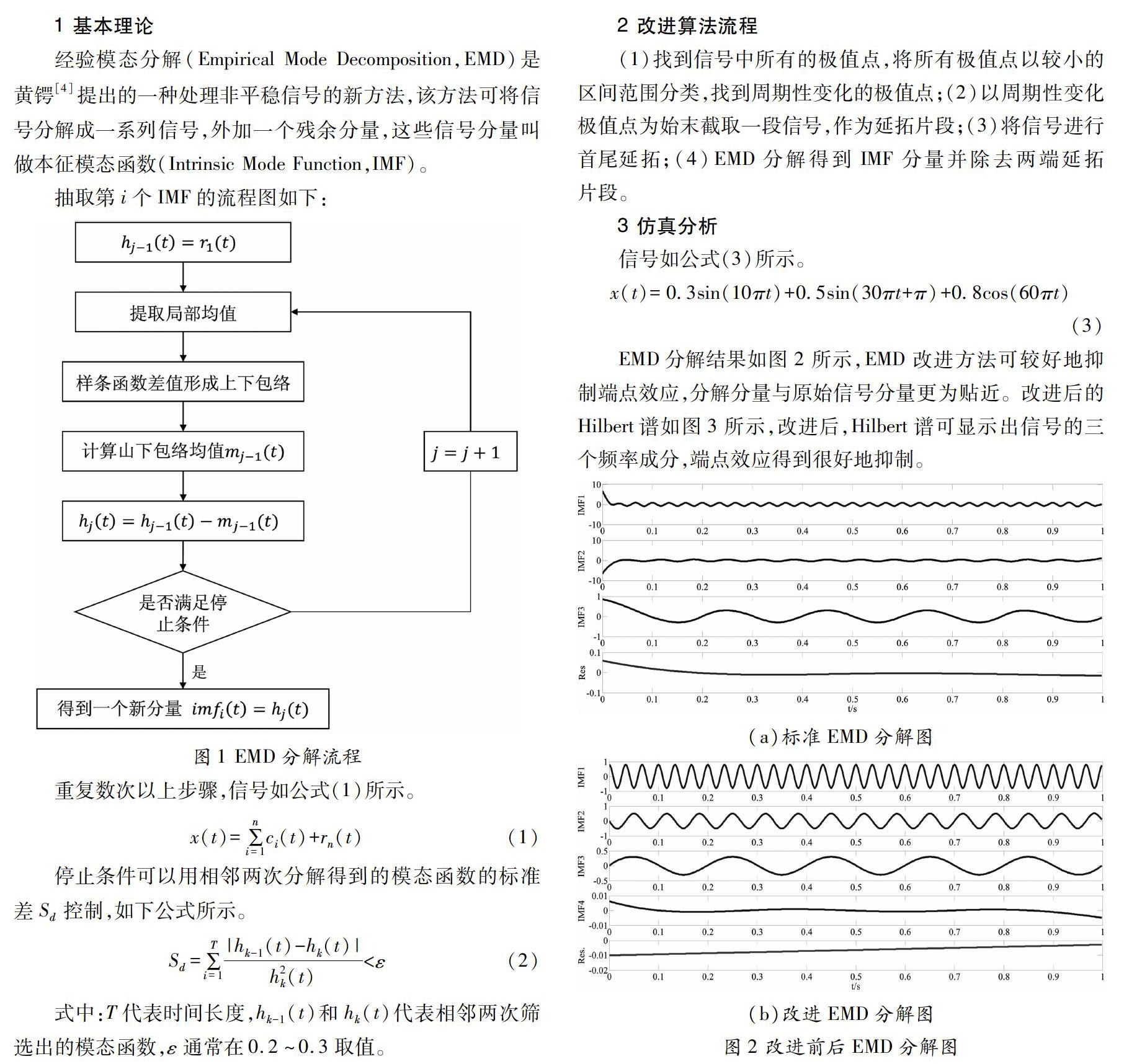
1 基本理论

经验模态分解（Empirical Mode Decomposition，EMD）是黄锷[4]提出的一种处理非平稳信号的新方法，该方法可将信号分解成一系列信号，外加一个残余分量，这些信号分量叫做本征模态函数（Intrinsic Mode Function，IMF）。

4 实例分析

美国凯斯西储大学轴承中心实验台如图4所示，本章节选用SKF6205驱动端轴承滚动体损伤振动数据，滚动体损伤直径l为0.1778mm，装置转速为1797r/min，采样频率为12Khz，载荷为0HP，轴承外圈直径为51.9989mm，内圈直径为25.0012mm，节径为39.0398mm，滚珠直径为7.9400mm，滚珠个数为9，接触角度为0。

时域信号及频谱如图5和6所示。故障频率蕴含在第五阶IMF分量中，理论值为141.09Hz，改进前后IMF5频谱如图7所示，改进后故障频率较改进前（153.84Hz）更接近理论计算值。

5 结论

本文提出了循环平稳周期延拓的EMD改进方法，利用仿真信号和轴承故障信号验证方法的有效性，改进方法所得故障频率较传统EMD方法更接近理论计算值，为旋转机械故障诊断提供了一种理论参考。

参考文献：

[1]Smith，Jonathan S.The local mean decomposition and its application to EEG perception data[J].Journal of The Royal Society Interface，2005，2（5）：443-454.

[2]Lei Y，Lin J，He Z，et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery[J].MECHANICAL SYSTEMS AND SIGNAL PROCESSING，2013，35（1-2）：108-126.

[3]Cheng J，Yu D，Tang J，et al.Local rub-impact fault diagnosis of the rotor systems based on EMD[J].Mechanism and Machine Theory，2009，44（4）：784-791.

[4]Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings A，1998，454（1971）：903-995.