基于影响矩阵法的系杆拱二次调索施工监控研究

王泽华，吴 凡

（中交第二公路勘察设计研究院有限公司，湖北 武汉 430050）

下承式钢管混凝土系杆拱桥为内部多次超静定而外部整体简支的无推力自平衡体系桥梁结构。主梁的自重及二期恒载主要由吊杆来承担，吊杆的拉力传递至主拱肋使其受压产生对主梁的推力，此推力由主梁内的纵向预应力体系来平衡。主梁、吊杆和拱肋三部分结构紧密协作而相互影响，吊杆位置和长短各异，吊杆力也相互影响，并决定了主梁和拱肋的受力和变形。吊杆力反复调索不仅施工过程复杂且对桥梁结构受力不利，固二次调索应合理规划调索方案，使成桥吊杆力经一次终调即达到设计吊杆力精度要求。

影响矩阵法在系杆拱桥二次调索应用较广，李洪波等人利用刚性吊杆法计算出吊杆内力与主梁控制节点的竖向位移从而得到其影响矩阵，然后运用自动调索法计算吊杆内力[1]。孔繁龙分别对每一吊杆增加单位吊杆力，然后求出每一阶段其他各吊杆点吊杆力的变化量推列出各吊杆之间的影响矩阵，然后利用惩罚函数法求解[2]。通用的影响矩阵理论较复杂，且多阶次矩阵方程的求解繁杂，实际应用不便。本文以某主梁刚度和活载均较大的系杆拱桥二次调索施工监控计算为例，利用桥梁专业工程软件MIDAS/CIVIL来确定系杆拱桥吊杆间的吊杆力影响矩阵，并利用数学计算软件MATLAB求解二次调索吊杆张拉力相关的影响矩阵方程，指导吊杆张拉施工。对此类主梁在活载作用下线形要求较高的拱桥的调索计算是快捷和准确的，可使成桥状态下各吊杆的吊杆力均处于均衡状态。

1 影响矩阵法原理

绝大多数下承式钢管混凝土系杆拱桥二次调索前拱肋和主梁的临时支架已经拆除，各吊杆具有初始吊杆力，桥梁完成了体系转换。二次调索的目的是使各吊杆力达到阶段目标值，并最终与成桥吊杆力相一致。

在二次调索计算前需要已知系杆拱桥二次调索前的吊杆力Tc和二次调索后的目标吊杆力Tm，拟定合理的调索顺序，在系杆拱桥二次调索之前分别给每根吊杆施加单位力，计算出该单位力对结构指定物理量的改变量，得出物理量的相关影响矩阵。通过影响矩阵法计算出在调索各阶段当前吊杆的施调量Ts，找出最优调索顺序，保证结构最安全的情况下使得调索施工后的吊杆力与设计目标值的误差在允许范围内。影响矩阵[A]可写成：

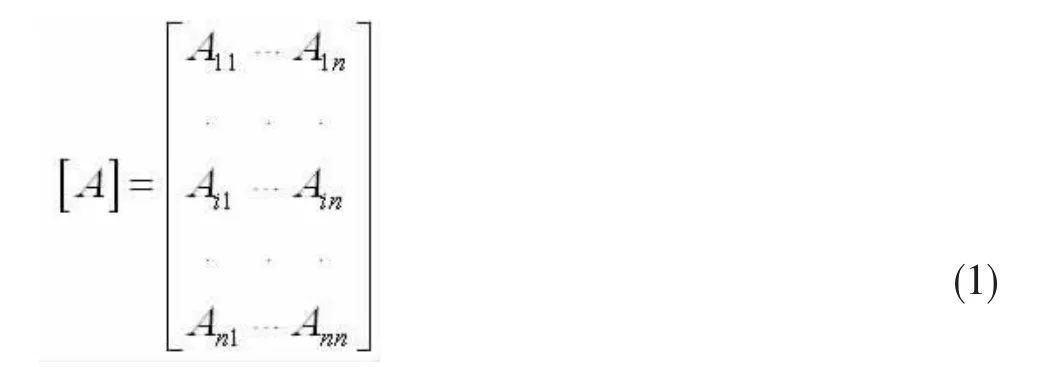
式（1）中Ain代表的是对吊杆n施加单位力后对吊杆i的影响系数，即第n列代表吊杆n单独受单位吊杆力对其他各吊杆的影响系数。施调量为：

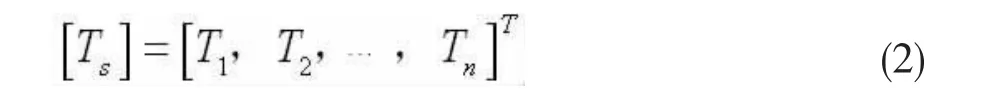
式（2）中Tn代表的是按照调索顺序一次张拉吊杆n时吊杆需要调整的量。受调量：

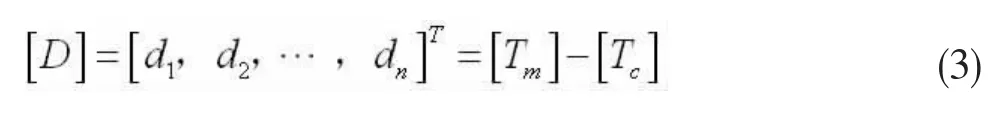
则影响矩阵方程表示为：

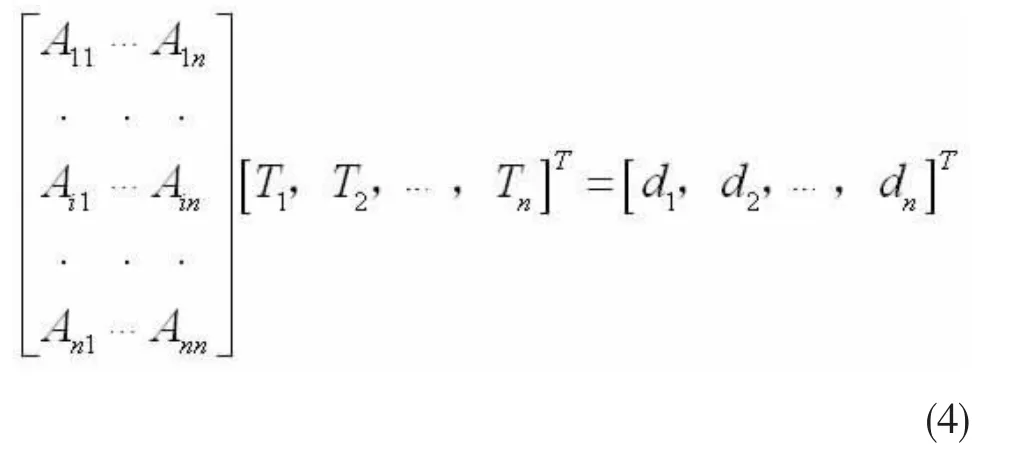
2 工程概况

某下承式钢管混凝土系杆简支拱桥，主拱理论跨度118.0m，矢高23.6m，单箱三室预应力混凝土箱型截面的主梁长122.0m，高3.0m。主拱为等截面钢管混凝土哑铃形平行拱，矢跨比为1/5，拱轴线采用二次抛物线，全桥共设18对127-Φ7镀锌高强钢丝材质的吊杆。全桥轮廓图如图1所示。

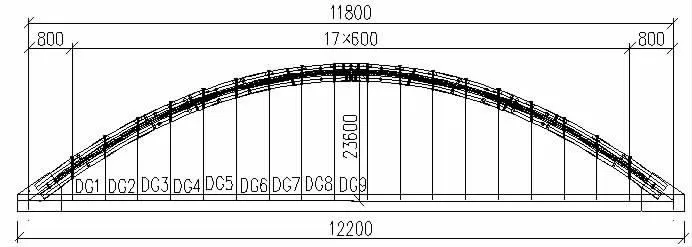
图1 全桥轮廓图(单位：cm)

施工监控中根据吊杆二次调索施工过程中测得的主梁应力与变形数据，随时分析各张拉阶段主梁内力、变形与设计预期值的差异并找出原因，提出修正对策，以确保成桥内力和外形曲线与设计值相符合。

3 影响矩阵及施调量计算

3.1 全桥模型的建立及技巧

采用桥梁专业工程软件MIDAS/CIVIL建立有限元模型，全桥建立共503个节点和611个单元，主梁和拱肋及拱肋支撑均采用梁单元模拟，全桥36根吊杆采用只受拉桁架单元模拟，图2为计算模型。

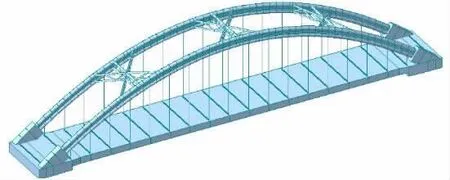
图2 MIDAS/CIVIL模型示意图

为方便后续计算吊杆力影响矩阵，按照如下施工顺序建立模型施工阶段：浇筑主梁并张拉第一批预应力→架设主拱调整拱肋线型→主梁第二批预应力张拉→拆除拱肋临时支架并泵送拱肋管内混凝土→安装吊杆进行初张拉→第三批预应力张拉→拆除主梁下满堂支架、施加二期恒载→二次调索。将每根吊杆的二次调索张拉顺序及张拉力定为一个施工阶段，结果中逐阶段提取吊杆力增量后组成矩阵形式再进行归一化处理即得到影响矩阵。由于模型中各吊杆初始张拉1000KN后吊杆力因相互影响而索力变化，为保证成桥后吊杆力均衡则必须进行二次调索。鉴于本桥主梁的刚度较大，利用主梁能量法最小原理拟定最优二次调索张拉顺序为：DG1→DG2→…→DG9，即由两侧向中间对称张拉。假设各吊杆二次调索的张拉力为1000KN，此张拉力仅为了建立完整的施工阶段，以便在后处理过程用于提取吊杆力影响矩阵。

二次调索前的吊杆力施工监控实测值非常重要，调索后吊杆力目标值是确定的，调索前的吊杆力目标值与实测值的差值即为调索的受调量，决定吊杆二次调索的施调量。而实际监控中发现每根吊杆的制造安装或锚头锚固等各施工因素影响都可能造成各吊杆的K值与理论值存在偏离，因此二次调索时必须以吊杆力实测值为准，从而在二次调索的施工监控过程中消除这类误差。

3.2 影响矩阵的提取

软件在后处理中选择结果→索控制→未知荷载系数→点击添加。项目名称上输入未知荷载系数，步骤名称选择吊杆二次张拉顺序的最后张拉吊杆的阶段，约束条件把各吊杆输入并选择桁架单元。约束条件依次选上对勾，“阶段/步骤”依次把吊杆二次张拉选择上，点击联系方程方法，点击求未知荷载系数。点击后对话框下边的“影响矩阵”即可得到影响矩阵，经整理得到对角线是1的影响矩阵，因篇幅所限只列出9组吊杆力的影响矩阵，见表1。同理可得关键截面应力影响矩阵和竖向位移影响矩阵。

3.3 吊杆力施调量的计算

利用MATLAB可以简单快捷地计算与施调量相关的影响矩阵方程。再将吊杆力施调量重新输入MIDAS/CIVIL模型中各二次调索顺序工况的施工阶段中进行计算，检查各吊杆张拉阶段吊杆力、主梁内力和竖向位移是否符合规范要求。基于影响矩阵法的线性求解往往只需经过有限次对受调量相关影响矩阵方程的迭代计算即可得到满足5%吊杆力误差限的二次调索施调量。需要注意的是，千斤顶及油压必须准确标定且配套使用，严格按照拟定的吊杆张拉顺序和二次张拉吊杆力进行张拉施工，施工监控过程中油压表读数与索力检测仪结果相互校核，保证施工质量。

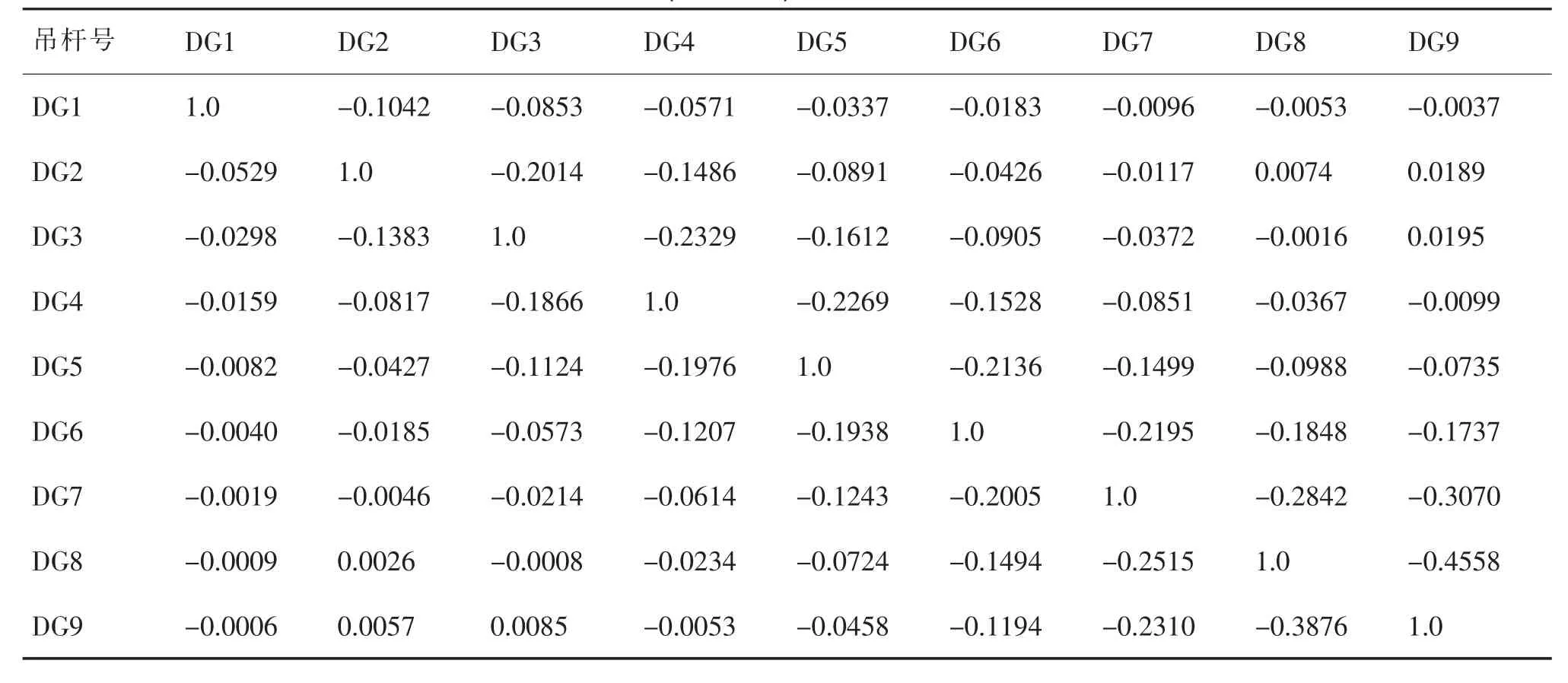
表1 9组（共18组）吊杆力影响矩阵

4 调索结果分析

根据最优张拉顺序以影响矩阵法得到的吊杆二次张拉力与成桥设计吊杆力值的对比见表2。

由表2可知，影响矩阵法有限元模型计算得到的成桥吊杆力与设计值近乎一致，表明施调量计算准确。由该组施调量按拟定调索顺序施工后对成桥吊杆力与设计值对比如图3所示，上下游吊杆力与设计值误差均小于5%，吊杆力二次调索达到了施工监控的预期目标。

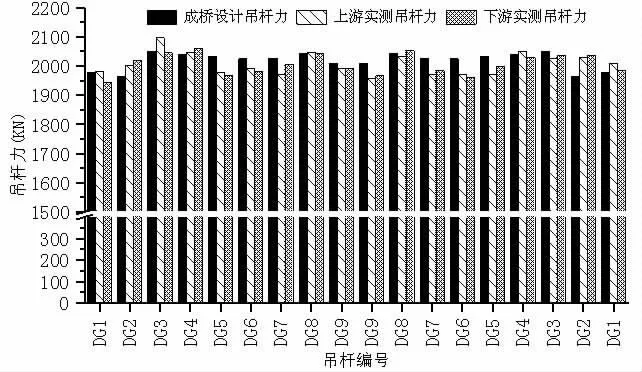
图3 成桥设计吊杆力与实测吊杆力对比

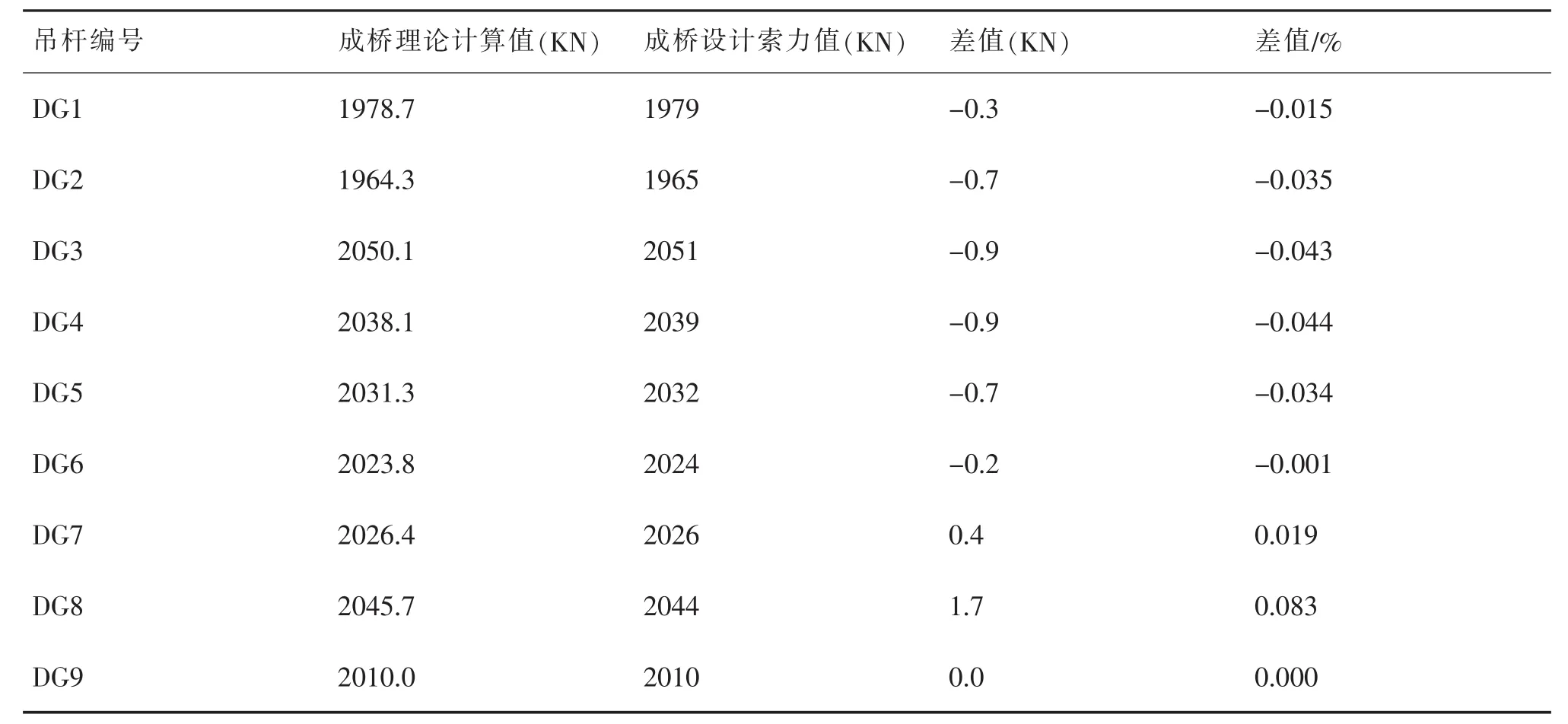
表2 成桥吊杆力理论计算值与设计吊杆力值相对比

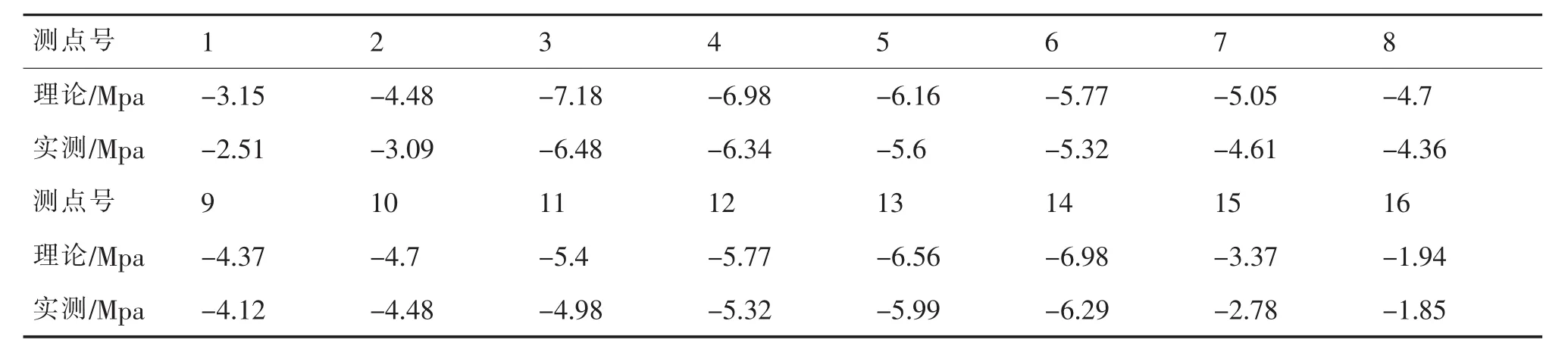
表3 二次调索后成桥主梁应力监测结果

再者，由表3主梁内埋置式钢筋应变计的应力监测分析结果可知，二次调索后成桥状态主梁应力累积值小于理论计算值，表明实际结构响应比预期小，更趋于安全状态。同时，成桥状态主梁线形监测结果也表明主梁累积预拱值较理论计算值更大，梁体具有更好的长期下挠富余度。

5 结论

本文采用桥梁计算软件MIDAS/CIVIL计算下承式钢管混凝土系杆拱桥二次调索的吊杆影响矩阵，辅以数学软件MATLAB求解与吊杆力施调量相关的影响矩阵方程，计算准确快捷，结果与设计值误差小。施工监控中成桥主梁应力和线形状态良好。可作为同类系杆拱桥二次调索的最优调索顺序及吊杆张拉力的施工监控计算之实用方法。