基于MATLAB 的传热学课程虚拟仿真实验平台设计

张程宾，韩 群，陈永平,2

（1. 东南大学 能源与环境学院，江苏 南京 210096；2. 苏州科技大学 环境科学与工程学院，江苏 苏州 215009）

传热学是一门研究由温差引起的热能传递规律的科学。传热学的研究方法主要有实验测定、理论分析和数值模拟[1]，其中测定实验教学因受经费、教学学时和实验仪器的限制，传热实验在可控和实验现象可视化方面往往不能满足教学要求。由于实际传热问题的复杂性，用理论分析方法也很难得出能量方程这一类偏微分方程的解析解[2]。数值模拟方法因具有教学成本低、可视化效果好、便于学生理解和运用等优点，在传热学课程教学上得到了重视。

在对传热问题的数值模拟软件中，MATLAB 具有显著的数值分析和图形处理能力，适用于求解传热问题的偏微分方程[3]。为此，本文采用MATLAB 软件对一维和二维热传导问题的有限差分法进行求解，通过MATLAB 图形用户界面（graphics user interface，GUI）开发了传热问题数值求解的虚拟实验软件，对热传导问题实现数据输入、回调运算、数据输出和结果显示功能。通过对不同条件下一维和二维热传导问题进行数值模拟，强化了学生在传热学课程上对该知识点的学习，提高了传热学课程的可视化教学效果。

1 传热方程的数值求解

传热问题数值求解的基本思路，是将导热物体在时间和空间上连续的温度场用有限个离散点的值代替，并采用有限差分和有限体积等数值方法建立离散值集合的代数方程，通过求解代数方程来获得离散点上温度的值[4-5]。如图1 所示，用与坐标轴平行的网格线划分求解区域，网格线间的交点称为节点，相邻节点之间的距离称为步长。

图1 网格划分

1.1 建立数学模型和区域离散

二维非稳态导热微分方程的一般形式为[6]：

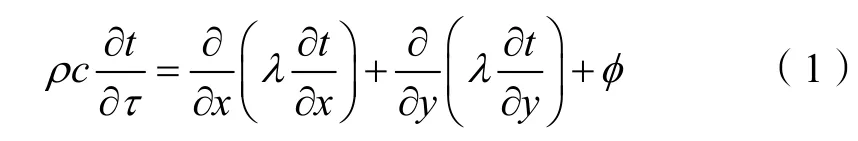
式中，ρ为微元体的密度、c为微元体的比热容、λ为微元体的导热系数、τ为时间、t为温度、φ为源项，x和y表示水平和竖直方向的节点坐标。当左端时间项设置为0 时，为稳态导热微分方程；只考虑x方向的热传导时，为一维非稳态的导热微分方程。对于内部节点离散方程，可以采用泰勒级数展开法进行建立：

相应的代数方程求解格式分别为显格式和隐格式。

取水平和竖直的网格步长Δx=Δy，对于显格式求解方法，联立方程（1）、（2）、（3）、（4），可得内节点的离散方程

同理，对于隐格式求解方法，联立方程（1）、（2）、（3）、（5）可得内节点离散方程：

1.2 边界条件处理

由于含有未知的边界温度，内节点建立的代数方程组是不封闭的，需要给定边界节点方程。常见的导热问题有3 类边界条件：规定边界的温度（第一类边界条件）、规定边界的热流密度（第二类边界条件）和规定表面传热系数h及周围流体的温度tf（第三类边界条件）[7]。

边界上的节点（m,n）如图2 所示。由能量守恒定律可得离散方程组

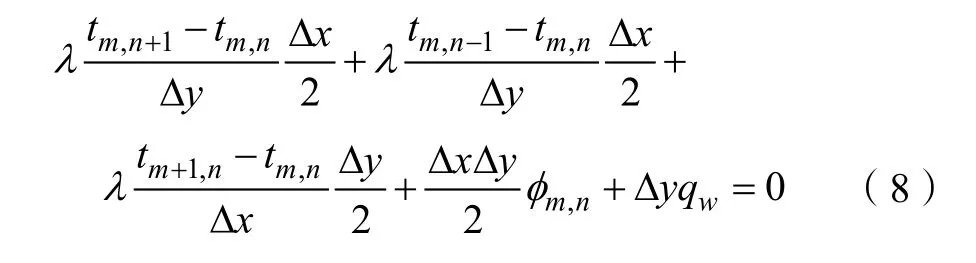
图2 边界上的节点

当边界条件为规定温度值时，可以对方程组直接求解并得到温度场的分布。当给定的边界条件为第二类或第三类边界条件时，需要分别进行讨论：

（1）第二类边界条件：规定传入计算区域的热量为正，此时将给定的热流密度值q代入式（8）进行求解；当给定的是绝热边界时，可令式中

2 编程依据的算法流程

如图 3 所示，基于 MATLAB 的传热学课程虚拟仿真实验平台的软件算法[8-9]求解基本流程如图3 所示。

图3 求解基本流程图

（1）根据实际物理问题建立数学控制方程，例如在一维非稳态导热问题中，左端为恒定热流，右端为与外界环境对流换热求解，数值求解不同时间下的温度分布。

（2）确定边界条件和初始条件，在GUI 界面上输入初始温度、热扩散率、环境温度、长度和时间等参数数据[10-12]。

（3）划分网格并对区域进行离散化，建立代数方程。

（4）设立初值并进行迭代求解，当满足收敛要求时将显示计算结果，如图4 所示。

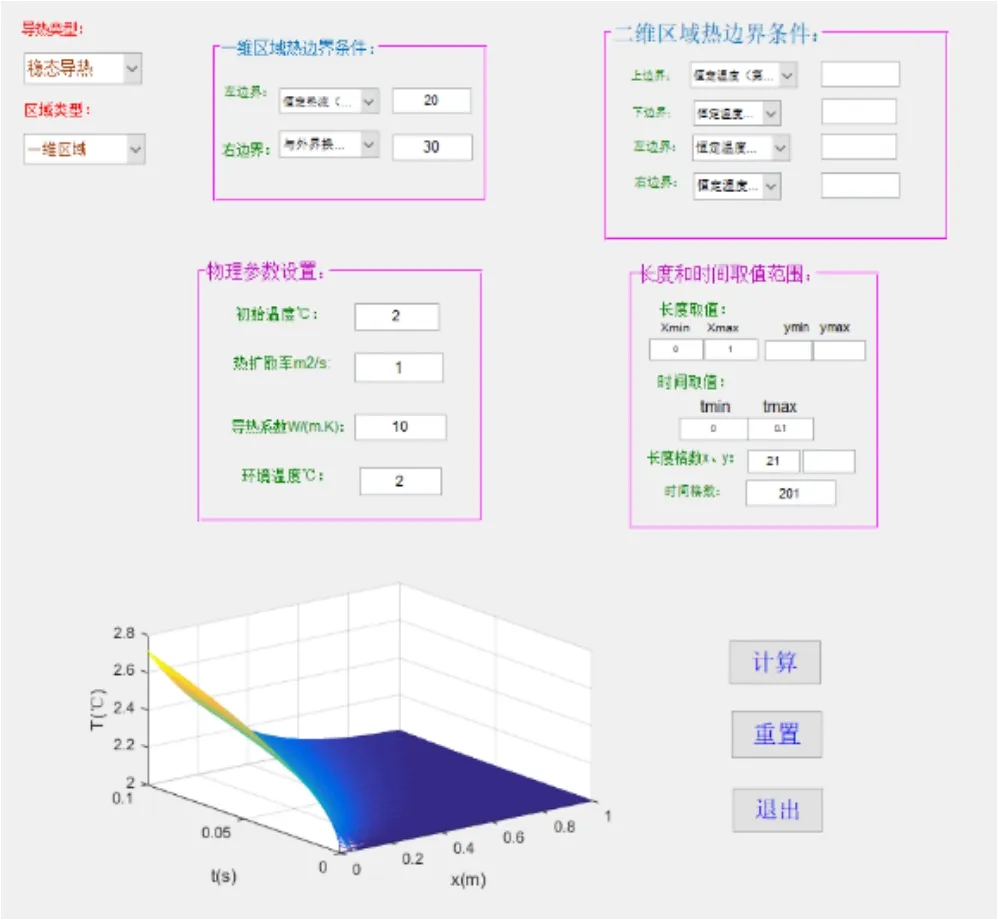
图4 仿真实验计算结果

3 功能模块介绍

传热学课程的虚拟仿真实验平台分为2 个模块：一维区域传热模块和二维区域传热模块，每个模块又根据导热类型分为稳态传热和非稳态传热，根据边界条件分为3 类热边界条件（恒定温度、恒定热流和对流换热）。在各个模块下设立弹出式选单，通过模块的选项在面板中设置参数，从而进入选定的模型中进行虚拟仿真模型计算。

3.1 一维区域传热模块

一维区域传热模块包括一维稳态传热模块和一维非稳态传热模块，在选定区域和导热类型后，设置热边界条件、物性参数和空间区域(非稳态需要划分时间)，再通过点击“计算”按钮以对一维传热问题进行求解，计算的温度分布图显示在坐标轴上[13-14]。

3.1.1 数学模型

以一维非稳态问题为例，取边界条件为恒定温度的一维非稳态导热，相应的数学表达式如式（9）所示：

在数值计算中需要采用的物理参数如表1 所示。

表1 一维非稳态导热问题的物理参数表

对于本问题的解析解为：

式中a为热扩散系数：

取时间t=0.1 s 时的温度分布进行数值计算结果与精确解析解的对比。如图5 所示，二者的结果非常接近，表明了数值计算结果的正确性。

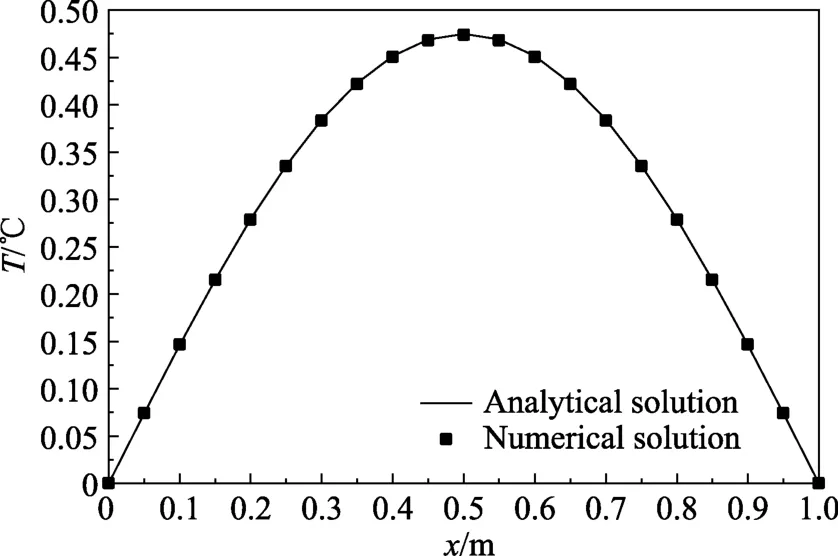
图5 t=0.1 s 时数值解与分析解对比图

3.1.2 GUI 运行结果与分析

在数值计算过程中，分别设定时间为 0.005 s、0.025 s、0.05 s、0.1 s 和 100 s。在 GUI 的坐标轴上温度分布图如图6 所示。

图6 一维区域非稳态传热的温度分布

选取每个设定时间最后的运行结果进行对比分析，其结果如图7 所示。仿真结果表明：在一维非稳态导热的初期，受边界低温的影响，物体靠近边界的温度较低，中间段的温度较高。随着时间的推移，非稳态导热过程继续进行，物体的温度持续下降，最终物体内部各处的温度无限接近于给定的边界温度。

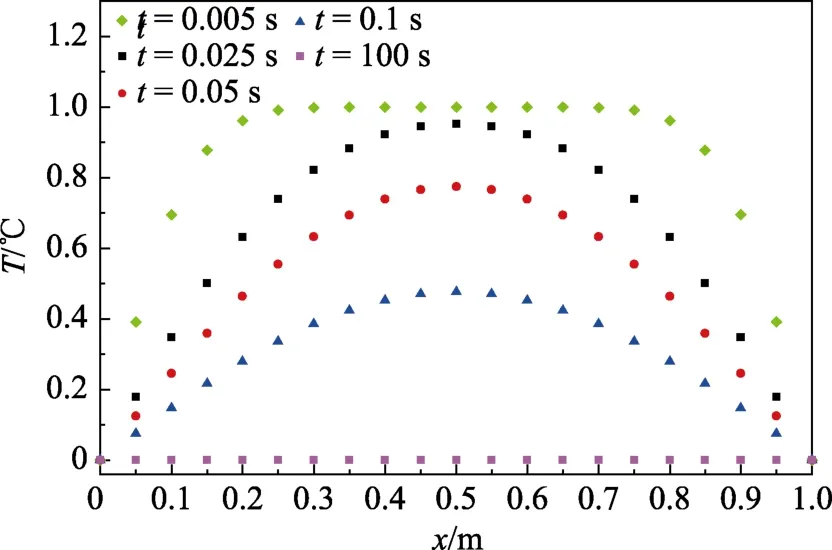
图7 不同时间的数值计算结果

通过本模块的演示，学生可以学习到一维稳态和非稳态传热的基本规律，认识到一维区域内温度的演化过程，掌握边界条件和物性参数的因素对传热效果的影响。

3.2 二维区域传热模块

二维区域传热模块包括二维稳态传热模块和二维非稳态传热模块，相关的GUI 数值模拟计算步骤与一维区域传热模块的计算步骤类似：选定区域和导热类型，设置热边界条件、物性参数和空间区域（非稳态需要划分时间），再点击“计算”按钮以对二维传热问题进行求解[15-16]。

3.2.1 数学模型

以二维非稳态传热问题为例，二维区域传热模块的功能的物理量参数如表2 所示。

表2 数值计算中的物理量参数表

3.2.2 GUI 运行结果与分析

在 GUI 的时间划分面板上，分别设定时间t为2.5×10-4s、5×10-4s、0.001 s、0.005 s、0.025 s 和 0.05 s进行仿真。二维区域非稳态传热的温度分布模拟结果如图8 所示。图中矩形区域内的温度分布随不同时间设定变化，说明温度的传递是从左端逐渐向内部传递，并通过一定时间的热传导，温度场的分布达到稳定状态。这是因为在矩形二维非稳态导热问题中，右边界设置为第三类边界条件（固体表面与周围流体间换热），下表面设置为绝热边界，上边界和左边界为第二类边界条件（恒定热流密度）且左边界热流远大于上边界热流，所以二维区域的热源输入主要由左端提供。在整个传热过程中，越靠近左边界的温度越高。

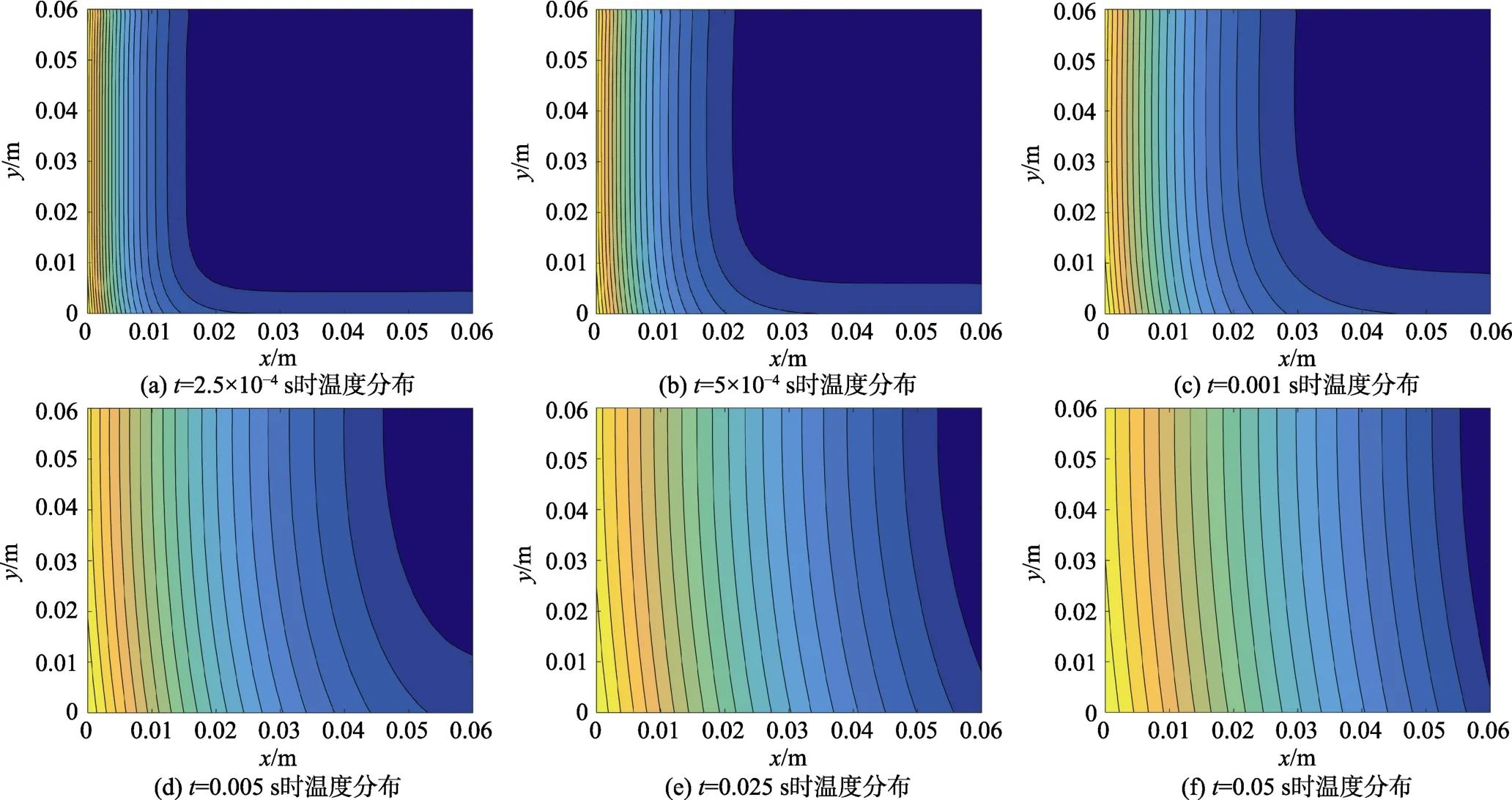
图8 非稳态传热条件下矩形区域的温度分布

随着时间的推移，在矩形区域内通过热传导方式传递热量，温度由左边界向内部传递，最后达到稳定的温度分布。

通过本模块的学习，学生可以仔细观察二维条件下温度场演化过程，掌握边界条件对导热的影响规律。

4 结语

基于 MATLAB 的传热学课程虚拟仿真实验平台实现了一维和二维区域传热的稳态/非稳态传热数值模拟和结果可视化动态演示，通过与解析解对比，验证了该虚拟仿真实验平台运算的可靠性。

虚拟仿真传热学实验具有可视化效果好、操作简单、价格低廉、运算准确、高效的优势。将虚拟仿真实验软件应用于传热学的课程中，有助于学生对传热问题的数值求解思路和方法的理解，同时也学习了MATLAB 在数值求解上的编程应用和 GUI 的设计，具有较高的教学实用性。