基于应力和时间双重影响下岩石蠕变模型研究

刘文博，张树光

(1.广西岩土力学与工程重点实验室，广西桂林，541004；2.桂林理工大学土木与建筑工程学院，广西桂林，541004；3.辽宁工程技术大学土木工程学院，辽宁阜新，123000)

随着深部煤岩的开采以及深部地下工程的建设，造成岩体变形破坏的原因越来越复杂，例如，当岩石处于不同应力状态或沿着不同应力路径加载和卸载时，岩石所呈现出的力学特性截然不同；当岩石内部含有节理面时，它的破坏形式与完整岩石破坏形式就有所差异。而经典的黏弹塑性理论不能较好地确定和预测多种因素影响下岩石的力学和变形特性，进而导致在工程实际中巷道支护失稳等重大问题得不到有效解决[1-3]。为了有效地解决上述问题，分析干扰因素对岩体性质的影响机制，在连续性力学理论基础上引入损伤变量反映岩体在地质作用下力学特性的变化规律[4-7]，进而构建损伤蠕变模型，可以较好地描述岩石蠕变全过程[8]。YANG 等[9]将岩石非线性流变模型中的传统黏性元件都以分数微分元件代替，并将传统模型的黏性系数变换为与应力和时间相关的函数，建立了岩石的非线性变参数蠕变模型；ZHANG 等[10]开展了滑坡潜在滑动面关键单元岩石的剪切蠕变特性试验，提出了一种新的塑性非线性模型(PFY 模型)；何志磊等[11]认为将传统西原模型中的整数阶牛顿黏壶替换成分数阶黏壶，且将改进后分数阶蠕变模型的参数非定常化，进而得到了分数阶变参数蠕变模型；韩阳等[12]将蠕变变形进行分段，采用改进流变方程的方式，得到岩石的时效性蠕变模型；刘开云等[13]提出了确定岩石初始屈服强度的方法，并定义了过应力的概念，得到弹性模型、黏聚力和内摩擦角与过应力差和时间乘积的函数，进而构建了非线性蠕变模型；HOU 等[14]提出了通过蠕变参数的变化来预测不同初始损伤状态下砂岩蠕变特性的方法，不仅可以描述3个典型的蠕变阶段，还可以反映初始损伤对岩石蠕变蠕变特性的影响。以往对于岩石损伤蠕变模型的构建过程中，较少考虑如何通过模型自身确定蠕变模型参数，即大多数研究成果只是利用损伤理论来建立损伤蠕变本构模型，且通过第三方拟合软件反演模型的参数，将得到的参数反代入模型中，对比模型曲线和试验数据，该方法无法准确地求得蠕变参数，从而不能进一步分析岩石的蠕变特点及失效机制。为此，本文提出一种确定蠕变参数的方法，分析在不同应力作用下参数与时间的关系，进而建立一种新型的时效性蠕变模型，以及为巷道-支护系统安全性评估提供可靠依据。

1 岩石蠕变模型参数的确定

1.1 一维蠕变模型的建立

通过引入文献[15]中黏弹塑性模型，此黏弹塑性模型由开尔文模型和弹塑性损伤模型(图中黑色部分)组成，如图1所示。

图1 改进后的黏弹塑性蠕变模型Fig.1 Improved viscoelastic-plastic creep model

式中：E1为弹性体弹性模量；E2为黏弹性的弹性模量；η为黏滞性系数；D为损伤变量；σ为应力；ε为总应变；t为蠕变时间；σs为岩石的长期强度，一般可以通过岩石的等时应力-应变曲线确定。

引入KACHANOV蠕变损伤模型[16]，刻画岩石加速蠕变阶段损伤演化规律，即

式中：A为参数，A=(2ESKN)1/(N+2)；E为弹性模量；S，K和N均为材料参数，均可以由试验获得。

将式(2)积分得

式中：t*为岩石发生加速蠕变的时间。

若损伤发展到断裂状态，则D=1 所对应的时间为蠕变破坏时间tF；当时间发展到t=tF时，存在以下关系：

式中：tF为蠕变破坏时间。

将式(4)代入式(3)得到损伤模型为

式中：C为损伤影响参数，且C=1/(N+3)。

将式(5)代入式(1)得，改进后的岩石蠕变损伤演化模型为

蠕变变形进入加速蠕变阶段后，当t→tF时，岩石轴向应变ε1→∞，且dε1/dt→∞，故式(6)中σ≥σs的蠕变方程可描述岩石的加速蠕变变形特征。无加速蠕变变形时，可采用式(6)中σ<σs的蠕变方程描述蠕变曲线。

1.2 三维蠕变模型推导

一维蠕变模型转化为三维蠕变模型需要用到应力张量σij、球应力张量σm、偏应力张量Sij、应变张量εij、球应变张量εm和偏应变张量eij，，即[17]

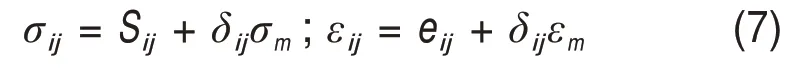
式中：δij为Kronecker 函数；球应力张量σm=(σ1+2σ3)/3；球应变张量εm=(ε1+2ε3)/3；Sij=σij-σm。

偏应力张量和球应力张量又可以表示为

式中：G1为剪切模量；K为初始体积模量。

本文的三轴试验为假三轴蠕变试验，则岩石在三维状态下蠕变模型为

式中：G2为黏弹性体的剪切模量；ε11为三维状态下的轴向应变；σ1为轴向应力；σ3为围压。

2 蠕变模型参数的确定

2.1 蠕变破坏时间tF和岩石发生加速蠕变的时刻t*

经典的岩石蠕变曲线示意如图2所示，由图2可以确定2个时间参数，即蠕变破坏时间tF和岩石发生加速蠕变的时刻t*。

图2 经典的岩石蠕变曲线Fig.2 Classic rock creep curve

2.2 剪切模量G1和体积模量K

岩石的瞬时应变包括弹性应变和塑性应变2部分。为了方便计算，假设岩石的瞬时应变都是弹性应变，则体积模量可由式(10)确定。将确定的体积模量值代入式(11)得到剪切模量G1。

式中：εV为体积应变；ε0为初始应变。

2.3 损伤影响参数C

损伤影响参数C是引入损伤变量时的1个试验参数。根据文献[18]可知，当黏弹性应变(开尔文体的应变)极限无穷大值时，存在以下关系：

在加速蠕变曲线上任意取2 个点(ti，εi)和(tj，εj)，时间点tj是在时间ti的30 min 范围内取得点，可认为在此小范围内岩石蠕变参数值为定值(即Ci=Cj)，则存在

式中：ε11i和ε11j为ti和tj时间下的轴向应变。

联立式(13)和式(14)，得到不同时间作用下参数Ci为

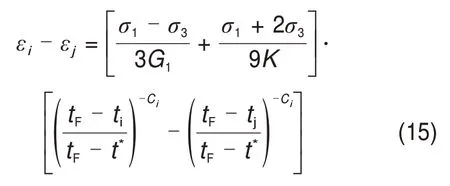
2.4 黏弹性参数G2和η

当σ≥σs时，在加速蠕变曲线上取n个点(ti，εi)，采用式(13)可以得到参数G2i为

在蠕变曲线上再任意取一个点(ti,εi)，存在

将确定的参数G2值代入到式(17)中，得到不同时间作用下黏滞性系数ηi为

综上所述，通过构建的损伤蠕变模型提出了一种新的确定蠕变参数的方法。

3 岩石三轴蠕变及三轴力学特性试验

3.1 岩石三轴力学特性试验

简单加工取出的岩体，并带回实验室进行精加工，制作成高h为100 mm、直径D为50 mm 的标准圆柱体，对外观具有明显缺陷的试样进行剔除。制备得到的标准岩石试样如图3(a)所示。

试验设备采用MTS815.02试验系统如图3(b)所示。岩石的三轴力学特性试验步骤如下：

1)将岩石试样两端均匀涂抹凡士林，保证测得试验数据不会受端部效应影响；

图3 砂岩试样和蠕变试验系统Fig.3 Sandstone sample and creep test systems

2)施加1个较小轴向应力，使岩石和试验机完全接触；

3)以200 N/s 速率将围压加载至预定值，且在整个试验过程保持围压不变；

4)以200 N/s 速率施加轴向应力直至岩石试样破坏为止；

5)采用位移控制方式施加轴向应变，直至岩石的应力-应变曲线出现一段峰后曲线时停止加载。

根据上述试步骤得出岩石试样在不同围压作用下的应力-应变曲线如图4所示。

3.2 蠕变试验方案

根据不同围压作用下的三轴压缩应力-应变曲线，确定不同围压作用下岩石的峰值强度。其中，当围压为20 MPa 时，岩石的峰值强度为112.3 MPa，第1 级应力水平取峰值强度的50%，即第1 级轴向应力为60 MPa(为了施加荷载方便取整数，下同)，以后每1级荷载分别增大5 MPa；当围压为30 MPa 时，岩石的峰值强度为138.5 MPa，第1 级应力水平取峰值强度的50%，即第1级轴向应力为70 MPa，以后每1 级荷载也分别增大5 MPa。当采用单试件分级加载进行岩石蠕变试验时，蠕变试验结果会受到历史荷载的影响，故采用Boltzmann叠加原理对试验数据进行处理，减小前期荷载对试验数据的影响，得到不同围压作用下岩石轴向蠕变历时曲线如图5所示。

图4 不同围压作用下的应力-应变曲线Fig.4 Stress-strain curves under different confining pressures

由图5可知：在同一应力水平作用下，围压越大，岩石的瞬时变形越小，说明增大围压可以有效提升岩石抵抗变形能力以及约束岩石的轴向瞬时应变；以围压20 MPa 为例，在应力水平分别为60，65，70 和75 MPa 时，砂岩瞬时变形依次为0.076 86%，0.114 5%，0.157 78%和0.230 44%；同时，岩石的瞬时应变与施加应力水平有关，随着应力增大，瞬时应变也逐渐增大，且瞬时应变与应力水平之间基本呈线性变化趋势；而瞬时应变占总应变的百分比却呈现先增大后减小的趋势，这是由于岩石自身内部具有大量孔隙，在加载初始时刻岩石孔隙先被压缩，待完全压密之后岩石内部裂隙才会大量产生，这导致岩石初期瞬时应变较大，后期瞬时应变较小。

在围压为20 MPa 时，岩石大约经历了4 个应力水平后才具有明显的加速蠕变变形，在围压为30 MPa 时，岩石大约经历了5 个应力水平后才具有明显的加速蠕变变形；在最后一级破坏应力水平作用下，岩石试样经历了较长时间的衰减蠕变和稳定蠕变后，才进入到加速蠕变变形阶段。

3.3 蠕变速率分析

采用式(19)拟合蠕变变形曲线，并对拟合公式进行一阶求导，进而得到1 条光滑的蠕变速率曲线。

式中：ε'为蠕变速率；a，b，c，d和e为拟合参数。

图6所示为20 MPa 围压作用下砂岩的蠕变速率。由图6可知：岩石在加载初始时都具有一个较大初始瞬时速率；当岩石变形由瞬时应变进入到衰减蠕变阶段后，蠕变速率开始急剧下降且逐渐衰减至零，当应力为60 MPa、时间约为39.1 h时，速率衰减到近乎为零，当应力为65 MPa、时间约为28.5 h时，速率衰减到近乎1个稳定值。

3.4 等时应力-应变曲线

岩石在围压20 MPa 条件下的轴向等时应力-应变曲线如图7所示。

由图7可知：当轴向应力小于70 MPa 时，各级荷载作用下的轴向应变随作用时间的变化很小(基本集中于1 点)，且应力-应变关系基本符合线性变化关系；当轴向应力大于70 MPa 时，随应力增大，岩石的轴向变形呈现出增大趋势，且应力-应变之间关系呈现出非线性变化规律。根据文献[19-20]可知，将发散点对应的应力作为岩石的长期强度，则围压20 MPa 条件下岩石的长期强度σs为70 MPa。因此，围压20 MPa条件下岩石的长期强度σs为70 MPa。

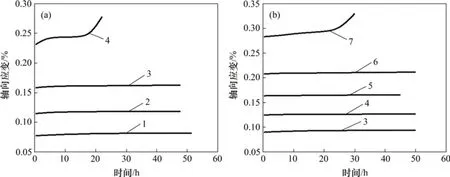
图5 不同围压作用下的轴向分阶段蠕变曲线Fig.5 Axial staged creep curves under different confining pressures

图6 20 MPa围压作用下砂岩的蠕变速率Fig.6 Creep rate of sandstone under confining pressure of 20 MPa

图7 围压20 MPa作用下岩石的轴向等时应力-应变曲线Fig.7 Axial isochronal stress-strain curve of rock under confining pressure of 20 MPa

4 蠕变参数变化规律与模型建立

4.1 蠕变参数变化规律

以围压20 MPa 的蠕变试验为例，通过不同时刻下蠕变参数的确定方法，得到围压20 MPa 的蠕变试验的模型参数，并绘制出蠕变参数随时间和应力变化的规律如图8所示。其中，体积模量K在不同应力作用下的变化规律差异较大，且体积模量K的变化规律直接反映了体积变形在应力和时间作用下的变化规律。当偏应力为65 MPa 时，体积模量K开始由正值向负值变化，故图8(f)中体积模量随时间的变化规律分为2段。对于剪切模量G1用线性拟合，其他蠕变参数均采用指数函数进行拟合，即

式中：g(·)为各蠕变参数关于时间t的函数；a1，b1，a2，b1和c2均为拟合参数。

由图8可知：当轴压为60 MPa 时，岩石处于压缩状态；当轴压为65 MPa 时，岩石逐渐由压缩状态转变成膨胀状态，K由正值向负值变化；当轴压大于65 MPa 时，岩石一直处于膨胀状态，但是体积模量K的绝对值越来越小，这说明岩石的扩容越来越明显。1)弹性剪切模量G1只与施加的应力偏量有关，且随着应力偏量增大，弹性剪切模量G1逐渐减小。2)S11/G1控制了试样轴向黏弹性应变量的发展趋势，通过拟合曲线可以发现随时间和应力水平增大，岩石的黏弹性应变也越大。3)S11/η(S11)控制了岩石黏弹性蠕变，岩石黏弹性蠕变随着时间逐渐减小且趋于1个稳定值，这表明岩石蠕变变形进入了稳定蠕变变形阶段。4)S11/C控制了蠕变变形过程中岩石内部损伤程度，随着S11/C增大，岩石的加速蠕变应变也增大，岩石的内部损伤程度也增大。

图8 不同时间作用下砂岩的蠕变参数变化规律Fig.8 Variation of creep parameters of sandstone under different time

综上所述，体积模量控制了岩石在蠕变过程中的体积变化(压缩与扩容)，但体积模量在不同应力作用下的变化规律难以采用1个统一的表达式进行描述；当岩石的体积压缩状态转化为扩容状态后，随蠕变应力增大，体积模量绝对值越小，且岩石的蠕变扩容效果随应力和时间的增大而越来越明显。损伤影响程度系数C控制了在蠕变变形过程中岩石内部损伤程度，C越大，证明岩石内部损伤越严重，且加速蠕变变形就越大，进而导致岩石更容易发生蠕变变形破坏。

4.2 考虑时间和应力影响的蠕变模型

根据图8中不同应力作用下各个参数与时间拟合曲线可知，蠕变参数经过拟合后的拟合参数如表1所示。

综上所述，考虑应力和时间对蠕变参数影响的蠕变模型如下。

当σ<σs时，

当σ≥σs时，

通过式(22)和式(23)绘制出模型曲线与试验曲线，如图9所示。由图9可知：蠕变模型曲线与试验曲线拟合度较高，这说明该模型较好地描述了岩石蠕变变形的全过程，且克服了西原体难以加速蠕变变形规律的缺点。同时，模型中蠕变参数与时间和应力的关系也较好地反映了岩石在蠕变加载过程中的劣化特性，从侧面证明了建立模型和确定蠕变参数的方法是合理的、正确的。

表1 不同应力作用下蠕变模型的拟合参数Table 1 Fitting parameters of creep model under different stresses

图9 不同围压作用下试验曲线和模型曲线的对比Fig.9 Comparison of test curve and model curve under different confining pressures

5 结论

1)体积模量控制了岩石在蠕变过程中的体积变化(压缩与扩容)，但体积模量在不同应力作用下的变化难以采用1个统一的表达式进行描述。

2)损伤影响程度系数C控制了在蠕变变形过程中岩石内部损伤程度，C越大，证明岩石内部损伤越严重，且加速蠕变变形就越大，导致岩石更容易发生蠕变变形破坏。

3)蠕变模型曲线与试验曲线拟合度较高，说明该模型较好地描述了岩石蠕变变形的全过程，且克服了西原体难以加速蠕变变形规律的缺点。