考虑干密度影响的红黏土蠕变特性及蠕变模型研究

李娜，陈昌富，朱世民，毛凤山

(1.湖南大学建筑安全与节能教育部重点实验室，湖南长沙，410082；2.湖南大学土木工程学院，湖南长沙，410082)

红黏土广泛分布于我国湖广地区、云贵高原以及长江中下游地区，在分布区进行高速公路和铁路建设施工时，需要对红黏土进行夯实或碾压使其达到设计密实度。增大密实度能提高土体的强度[1-3]，而密实度对红黏土蠕变特性的影响直接关系到红土边坡的长期稳定性以及红土路基的长期沉降量，因此，研究干密度对红黏土蠕变特性的影响具有重要的工程意义。目前,有关干密度对土体蠕变特性影响的研究成果较少。王松鹤等[4]对不同干密度黄土的进行三轴蠕变试验，发现通过改善排水情况、增大土体密实程度能避免产生蠕变破坏。此外，史祥等[5]对不同干密度的分散性土进行三轴固结排水试验，发现分散性土干密度愈大，土体变形愈小，蠕变现象愈不明显。干密度对红黏土蠕变特性有很大影响，但用于定量描述该影响的研究较少。用于定量描述土体蠕变特性的蠕变模型主要包括元件模型和经验模型[6-8]。张先伟等[9]建立的经验型蠕变模型与Singh-Mitchell模型和Mesri模型相比，其对饱和软土蠕变特性的预测效果更好。陈昌富等[10]通过锚-土界面剪切蠕变试验建立了能同时描述衰减蠕变和加速蠕变的经验蠕变模型。罗庆姿等[11]建立了含分数阶导数的Merchant 模型，与原Merchant 模型相比，其拟合精度更高，更适用于长期变形预测。经验模型虽然简单实用，但拟合得到的模型参数和方程缺乏物理含义，而元件模型中的参数都具有明确的物理意义，且借助不同应力水平下蠕变试验曲线就能辨识元件模型的参数[12-14]。如金德海等[15]推导出Burgers 模型的三轴蠕变理论解，并通过模型参数辨识建立了一种考虑围压对粗粒土蠕变特性影响的修正Burgers 模型。本文作者利用改制的三轴蠕变试验装置，通过红黏土排水三轴蠕变试验，获得不同干密度下红黏土三轴蠕变试验曲线；然后，以试验曲线为依据，辨识Burgers 蠕变模型中的参数，得到模型参数随干密度的变化规律，从而建立一种用于描述不同干密度的红黏土蠕变试验曲线的Burgers 蠕变模型；最后，利用所提出的模型对试验结果进行预测分析，以验证本文模型的可靠性。

1 红黏土三轴蠕变试验

1.1 试验用料及装置

试验所用红黏土取自湖南省长沙市宁乡县某高速路段，通过XRD 测得该红黏土主要矿物成分为石英、高岭石、云母和赤铁矿。由标准击实试验测得红黏土的最大干密度为1.78 g/cm3，最优含水率为18%。土样的其他物理力学参数如表1所示，颗粒级配曲线如图1所示。

表1 红黏土的基本物理力学参数Table 1 Basic physical mechanical properties of red clay

图1 土的颗粒级配曲线Fig.1 Particle distribution of red clay

试验所用装置为自行设计改造的TSZ 应变控制式三轴仪，如图2所示。该装置由恒载系统和数据采集系统组成，具体原理见文献[16]。

1.2 试样制备及试验方案

试验所用试样为圆柱形土样，其直径φ=39.1 mm，高度h=80 mm。试样制备的具体步骤为：首先，配置含水率为18%的土料；然后，计算不同干密度的土样所对应的土料质量，称取设定质量的土料进行分层击实，击实后土样的干密度分别为1.49，1.60，1.65 和1.68 g/cm3；最后，对试样进行抽气饱和，并测得试样饱和后的含水率分别为29.8%，25.1%，23.5%和22.2%，由此制备不同干密度的饱和红黏土蠕变测试样。

图2 三轴蠕变试验装置Fig.2 Tri-axial creep testing device

试样制备完成后，先让其在200 kPa 围压下固结完成。然后，采用分级加载的方式进行蠕变加载，加载等级为8～10 级。本文选用的蠕变稳定标准为在10 000 s内试样的轴向变形小于0.01 mm[17]，由于红黏土强度高，压缩性低，试样在加载后基本能在24 h 内达到该稳定标准，故每级荷载的加载时间统一设定为24 h。

1.3 试验结果

根据上述试验方法开展不同干密度的红黏土三轴蠕变试验，得到分级加载全过程曲线。研究表明土体在外力作用下产生的变形包括固结变形和蠕变变形[16]，由于本文仅研究红黏土的蠕变变形，因而需消除试样在偏应力作用下的固结变形。为此，首先，采用“陈氏叠加法”[18]将红黏土试样的三轴蠕变分级加载全过程曲线转换为分别加载曲线；然后，利用文献[16]中方法消除固结变形，即可获得试样在分别加载条件下的蠕应变与时间的关系曲线(蠕变曲线)，如图3所示。

2 考虑干密度的红黏土蠕变模型

2.1 研究思路

图3 红黏土三轴蠕变分别加载曲线Fig.3 Triaxial creep loading curves of red clay

传统的Burgers 模型[19]是由Maxwell 模型和Kelvin模型串联而成的4元件黏弹性流变模型，其具体结构及物理特性如图4(a)所示。传统的Burgers 模型因能够较准确地描述各类岩土材料在衰减和稳态蠕变阶段的特性，在岩土工程中应用广泛，为此，本文建立考虑干密度影响的Burgers蠕变模型。

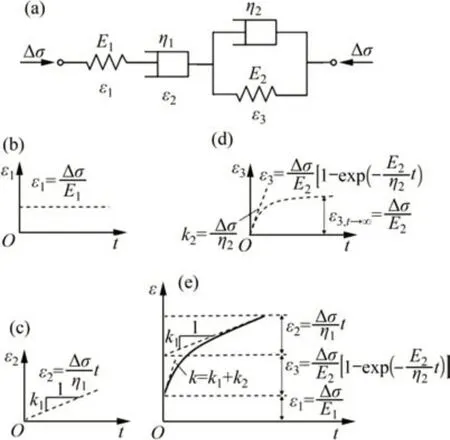
图4 Burgers蠕变模型Fig.4 Burgers creep models

Burgers 蠕变模型的蠕应变是由串联的弹簧体对应的瞬时弹性应变ε1、串联的黏壶体对应的等速应变ε2以及串联的Kelvin 模型对应的蠕应变ε3组成：

对式(1)求导，获得蠕变速率与时间t的关系：

下面对模型的边界条件进行分析。

当t=0时，

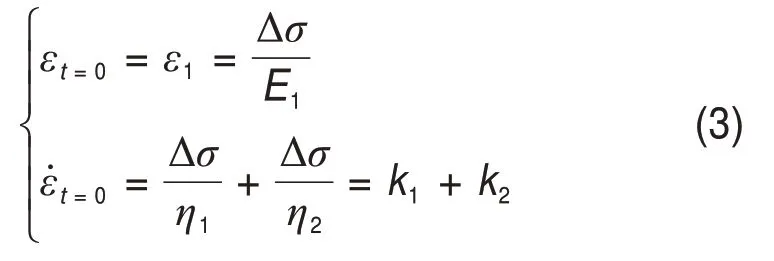
当t→∞时，

由式(3)和式(4)联立可得

式中：ε1为瞬时弹性应变；k1为蠕变曲线在时间t趋于无穷大时对应的斜率；k2为Kelvin模型对应的起始蠕变率；ε3,t→∞为Kelvin模型对应的最终应变。

参数ε1，ε3,t→∞，k1和k2均可根据实测的蠕变曲线确定，如图4所示。故可通过式(5)确定Burgers模型的4个模型参数。

选取部分蠕变试验曲线进行辨识，以确定参数ε1，ε3,t→∞，k1和k2，进而得到Burgers 模型的4 个模型参数；对4个模型参数与试样干密度和偏应力之间的关系进行回归分析，由此确定模型参数与试样干密度和偏应力之间的经验关系式；最后，将上述确定的经验关系式代入Burgers 蠕变方程，即可建立考虑干密度影响的Burgers蠕变模型。

2.2 模型参数的辨识

下面以干密度为1.68 g/cm3的红黏土试样的三轴蠕变试验结果为例，介绍Burgers 模型4 个模型参数的辨识方法。

2.2.1 弹性模量E1的辨识

由上述分析可知，ε1为试样加载瞬时所产生的应变，对应蠕变曲线(见图3)在初始时刻的轴向应变。瞬时弹性应变ε1与偏应力Δσ关系如图5所示。从图5可知：瞬时弹性应变ε1与偏应力Δσ大致呈线性关系，采用线性函数进行回归分析，结合式(5)，不难得出该回归直线的斜率为1/E1。

2.2.2 黏壶系数η1的辨识

图5 瞬时弹性应变ε1与偏应力水平Δσ关系曲线Fig.5 Correlation between instantaneous elastic strain ε1 and deviatoric stress Δσ

由图3可知：当偏应力Δσ较小时，试样产生衰减蠕变，蠕变应变渐趋于恒定，蠕变速率渐趋于0 min-1，即表明串联的黏壶体对应的等速应变ε2=0，k1=0 min-1；当偏应力Δσ超过某一水平(假定为σ0)时，试样产生等速蠕变，蠕变应变最终将呈线性增加，蠕变速率将渐趋于某一定值，由式(4)可知该定值为k1；随着偏应力Δσ继续增大，试样将产生加速蠕变，并最终产生破坏[20]。本文不考虑加速蠕变阶段，为描述试样的衰减和等速蠕变特性，引入开关函数并令

式中：σ0为试样产生等速蠕变的偏应力阈值。

由图3可知：当t>600 min 时，蠕变曲线近似为直线，由式(4)可知该直线的斜率为k1。等速蠕变速率k1与偏应力水平Δσ的关系如图6所示。从图6可知k1与偏应力Δσ大致呈线性关系，结合式(4)和式(7)发现该回归直线的斜率为1/η1。此外，回归直线与偏应力轴的交点即为σ0，本例中，σ0=75.1 kPa。

2.2.3 弹性模量E2的辨识

根据式(1)，将蠕变应变中的瞬时弹性应变ε1和等速蠕变段应变ε2去除，即得到Kelvin模型对应的蠕变应变ε3，ε3随着时间的增大逐渐趋于某一定值ε3,t→∞。统计不同偏应力Δσ下Kelvin 模型的最终蠕变应变ε3,t→∞如表2所示。由式(4)可知，弹性模量E2即为偏应力Δσ与ε3,t→∞的比值。弹性模量E2与偏应力水平Δσ关系曲线如图7所示。由图7可知E2与Δσ大致呈指数函数关系。采用式(8)进行回归分析，即可建立E2与Δσ的经验关系：

图6 等速蠕变速率k1与偏应力水平Δσ关系曲线Fig.6 Correlation between isokinetic creep rate k1 and deviatoric stress Δσ

表2 偏应力与Kelvin最终蠕应变Table 2 Deviatoric stress and Kelvin final creep strain

图7 弹性模量E2与偏应力水平Δσ关系曲线Fig.7 Correlation between elastic modulus E2anddeviatoric stress Δσ

式中：α和β为拟合参数，与试样的干密度有关。

2.2.4 黏壶系数η2的辨识

前面已获得Kelvin模型对应的蠕变应变ε3，由式(4)可知，蠕变应变ε3在初始时刻的曲线斜率即为k2。起始蠕变率k2与偏应力水平Δσ的关系如图8所示。从图8可见：k2与偏应力Δσ基本呈线性关系。采用线性函数进行回归分析，由式(5)可知，该回归直线的斜率为1/η2。

图8 起始蠕变率k2与偏应力水平Δσ关系曲线Fig.8 Correlation between initial creep rate k2 and deviatoric stress Δσ

按照上述方法对其他干密度的部分红黏土蠕变曲线进行分析，由此建立Burgers 模型参数E1，η1，E2和η2与偏应力Δσ之间的经验关系，并进一步获得用以表征上述经验关系的6 个参数E1，η1，α，β，η2和σ0，见表3。

2.3 考虑干密度影响的蠕变模型的建立

前面已建立Burgers 模型参数E1，η1，E2和η2与偏应力Δσ之间的经验关系，并获得了用以表征上述经验关系的6 个参数E1，η1，α，β，η2和σ0。若再建立出这6个参数与试样干密度ρd之间的经验关系，则可进一步建立Burgers 模型参数E1，η1，E2和η2与偏应力Δσ及干密度ρd之间的经验关系，由此可建立考虑干密度影响的红黏土蠕变模型。

模型参数与干密度关系曲线如图9所示。由图9可知：参数E1，η1和η2与干密度ρd均大致呈指数函数关系；参数α与干密度ρd大致呈线性关系；参数β与干密度ρd大致呈抛物线关系。参数σ0取平均值81 kPa，采用相应的函数形式对参数E1，η1，α，β，η2和σ0与偏应力Δσ之间的关系进行回归分析，建立这6 个参数与干密度ρd之间的经验关系(见式(9))，再将式(9)代入式(10)即可建立考虑干密度影响的Burgers蠕变模型。

利用上述建立的考虑干密度影响的Burgers 蠕变模型对用于模型参数辨识的红黏土蠕变曲线进行预测分析，结果如图10所示。由图10可知：当偏应力较小时，本文模型对蠕变曲线的预测效果较好；而随着偏应力增加，模型预测精度有所降低。但总体上，本文模型对参与模型参数辨识的红黏土蠕变曲线的预测效果较好。

3 预测效果分析

为进一步验证本文提出的考虑干密度影响的Burgers 模型的预测效果，对另一部分未参与模型参数辨识的红黏土蠕变曲线进行预测，结果见图11。由图11可知：本文模型对未参与模型参数辨识的红黏土三轴蠕变试验曲线的预测效果也较好。这进一步验证了本文模型的适用性和准确性。

表3 蠕变模型拟合参数值Table 3 Creep model fitting parameter values

图9 模型参数与干密度关系曲线Fig.9 Correlation between model parameters and dry density

图10 本文模型对参与参数辨识的蠕变曲线预测分析Fig.10 Predictive analysis of creep curves participating in parameter identification

图11 本文模型对未参与参数辨识的蠕变曲线的预测结果Fig.11 Prediction results of creep curves of model that are not involved in parameter identification

4 结论

1)为深入研究干密度对红黏土蠕变特性的影响，利用自行设计改造后的三轴蠕变试验装置开展不同干密度的红黏土三轴蠕变试验，获得不同干密度的红黏土试样的分别加载曲线。

2)基于Burgers模型4个模型参数的物理意义，对部分蠕变试验曲线进行模型参数辨识，以此建立考虑干密度影响的Burgers蠕变模型。

3)利用建立的考虑干密度影响的Burgers 蠕变模型对蠕变试验曲线进行预测分析，结果表明本文所建模型具有良好的预测效果，适用于描述该地区的红黏土蠕变特性。

4)重塑试样破坏了红黏土的结构特性，后续可进一步开展红黏土在原状及重塑状态下的蠕变对比试验，研究红黏土的结构性对其蠕变特性的影响。