随钻电阻率成像测井仪定量评价地层界面探究

康正明， 柯式镇， 李 新， 倪卫宁， 李 飞

（1. 陕西省油气井测控技术重点实验室（西安石油大学），陕西西安 710065；2. 中国石油大学（北京）地球物理学院，北京 102249；3. 中国石化石油工程技术研究院，北京 100101）

目前，国内外油田大都面临着低渗透油气藏的开发难题，低渗透油气藏地质情况复杂，为了解决这一难题，多采用定向井和复杂结构井进行开发。在钻进过程中，准确监测井下环境，及时获取井下工程参数和地质参数是保证钻进低渗透油气储层时井筒安全的前提，也是优快钻井、提高开发效益的基础[1]。其中，随钻测井技术具有重要作用，特别是随钻电阻率成像仪器为低渗透油气藏高效开发与钻井完井提供了丰富的地层信息，可以满足定向井在裂缝地层、薄层、低孔隙度和低渗透率地层等复杂储层中的地质导向、地层评价和井壁电阻率成像需求[2–3]。

随钻电阻率成像测井可以提供侧向电阻率、钻头电阻率和钮扣电极电阻率成像，但目前的研究主要集中在该仪器的探测特性和测量环境影响因素的数值模拟方面[4–12]。随钻电阻率成像测井仪在大斜度井、水平井中应用的报道较多，但大多是仪器在钻井完井和地质应用中的技术优势研究。笔者曾对钻头模式的探测特性和地质导向功能进行了数值模拟研究，并对钮扣电极探测深度和测量环境的影响因素进行了分析[13–15]。 李铭宇等人[16]对该类仪器侧向模式测量信号的影响因素和其探测特性进行了数值模拟研究。Jing Jiankun等人[17]对仪器的成像分辨率进行了考察。随着随钻测井仪器技术的进步，随钻电阻率成像测井仪器的探测深度较常规电缆式井壁电阻率成像测井仪器大幅提升，其钮扣电极在周向上分布的数量也在增加，使仪器在不旋转的情况下，利用其方位钮扣电阻率测量数据的差异识别地层界面成为可能，但目前尚未开展相关的研究。为此，笔者在简化随钻电阻率成像测井螺绕环激励源的基础上，以常见的随钻电阻率成像测井仪器为例，利用三维有限元方法模拟了仪器测井响应特征，考察了仪器在水平井和斜井中靠近和穿过地层界面时的测井响应特征，根据模拟结果建立了地层界面定量解释模型，并利用理论分析验证了地层界面计算模型的适用性。

1 螺绕环激励源测量原理

随钻电阻率成像测井仪器有2种激励机制，一种是直接给电极加载电流；另一种是将螺绕环套在钻铤上（见图1），给螺绕环施加交流电，其测量频率为1 kHz左右。钻铤对螺绕环感应电流进行导通，使其在螺绕环发射器上部和下部的钻铤上产生等量电位，以达到自动聚焦的作用，因此电流聚焦效果和侧向测井类似。第2种方法在工艺上容易实现，且钻进过程中仪器受到的磨损较电极方式小，因此被广泛应用[18]。

理论分析时，通常对图1所示的实体螺绕环进行简化处理，考虑测量频率时，发射螺绕环可以等效为理想化磁环，对螺绕环加载交流电。假定钻铤在井轴方向上无限长，井轴与柱面坐标系Z轴一致，可根据赫兹向量π描述其在空间产生的电场和磁场[19]，即：

图 1 螺绕环结构示意Fig. 1 Schematic diagram of the toroid coil structure

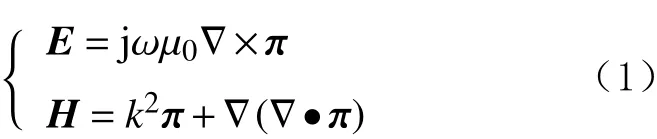
式中：E为电场强度，V/m；H为磁场强度，A/m；ω为角频率，rad/s；µ0为 相对磁导率；k为传播系数；j为虚数单位。

赫兹向量π满足波动方程：

式中：M为螺绕环的磁矩，A·m2；N为螺绕环匝数；I为加载的交流电流，A；A为螺绕环截面积，m2；r0为螺绕环半径，m。

由介质的连续性可知，磁场强度和电场强度的切向分量要连续。因此，介质为径向非均匀介质时，波动方程式（2）应满足以下边界条件：

式中：ρ为空间任意一点距离井轴的距离，m；E1z，E2z为电场强度的切向分量，V/m；H1φ，H2φ为磁场强度的切向分量，A/m。

求解波动方程式（2），可以得到赫兹向量π，进一步转化为磁场强度Hφ；利用楞次定律，可以得到接收螺绕环的感应电动势V，对感应电动势进行刻度，可以得到地层电阻率R。

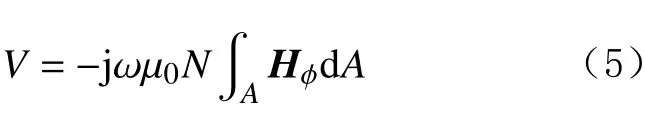
实际测量中，由于测量频率低（约1 kHz），因此在大多数情况下可以忽略频率的影响，将螺绕环等效为延长的电压偶极子。此时，与传统侧向测井测量原理相同，采用欧姆定律计算视电阻率Ra。

式中：Ra为视电阻率，Ω；K为仪器常数；U为发射螺绕环上、下钻铤产生的电压差，V；I为钮扣电极和接收螺绕环接收到的电流，A。

2 有限元数值模拟

上述理论分析是针对二维模型情况推导的解析公式，对于三维问题，随钻测井中经常采用的数值方法包括时域有限差分法、有限元法和有限体积法等，这些方法可用于复杂钻井环境的仿真[20]。随钻电阻率成像测井响应的数值模拟由于其模型尺寸变化较大，比如几厘米的钮扣电极和长达几米的测井仪器和地层，因此属于多尺度问题[21]。目前，大多数学者采用有限元法进行模拟研究，笔者也采用该方法，并建立了水平井和斜井三维有限元地层模型，考察随钻电阻率成像测井在地层界面的测井响应特性。

本文模拟随钻电阻率成像测井仪器的结构较为常见，由一个发射螺绕环T和2排直径分别为10 mm和25 mm的钮扣电极B1与B2组成（见图2）。其中，B1与T的源距小于B2与T的源距，B1的不同方位钮扣电极分别为1，3，5和7，B2的不同方位钮扣电极分别为2，4，6和8，分别按正北顺时针方向均匀分布在周向上。

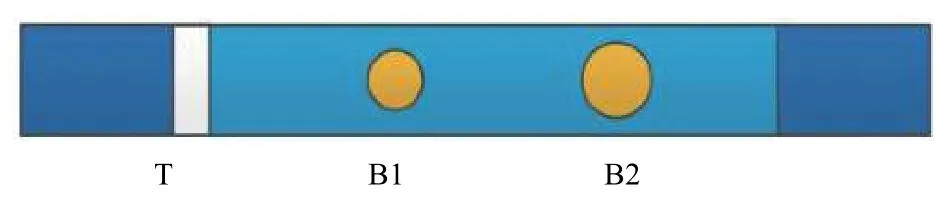
图 2 模拟仪器结构示意Fig.2 Schematic diagram of the analog instrument

为了简化模拟的复杂度，将钻铤视为理想导体，忽略测量频率的影响；采用直流源进行模拟，可以将螺绕环在钻铤和地层中产生电流的方式等效为一对延长的电压偶极子。模拟时，对发射螺绕环下方钻铤表面赋予固定的正电压，将其等效为延伸的正电压极子；对发射螺绕环上方钻铤表面赋予负电压作为回路，将其等效为负电压极子，二者中间有一个间隔，为发射螺绕环。电流从螺绕环下方钻铤出发，流经井眼和地层，然后再返回到其上方的钻铤中（见图3）。图3反映了等效激励源产生的电势和电流密度分布特征，图中色柱代表为电势，从0 V到1 V变化，可以看出这种激励方式的聚焦效果和侧向测井类似。将采集的钮扣电极表面电流代入式（6），即可将电流转换为地层视电阻率。

图 3 电位场和电流场分布特征Fig. 3 Distribution characteristics of potential field and current field

与电缆测井相比，随钻电阻率成像测井的优势是可以应用在大斜度井和水平井中，然而目前这方面的数值模拟研究较少，因此有必要考察其测井响应特征和影响因素。

2.1 水平井测井响应数值模拟结果

为考察仪器在水平井中的测井响应，建立了水平井模型。该模型由3层地层组成，上下为围岩，电阻率Rs为1 Ω·m，中间为目的层，电阻率Rt为10 Ω·m，钻井液电阻率Rm为0.1 Ω·m[15]。仪器位于目的层中，目的层厚度H为2.00 m，仪器的初始位置位于目的层中间，坐标为Z为0，向上靠近地层界面Z为正，向下靠近地层界面Z为负。仪器向上接近地层界面过程中，1号钮扣电极正对地层界面，与地层界面最近，而5号钮扣电极则距离地层界面最远，向下接近地层界面则情况相反。钮扣电极B1和B2不同方位视电阻率和仪器与地层界面的距离的关系如图4所示。

图 4 水平井中不同方位钮扣电极测井响应Fig.4 Logging response characteristics of different azimuthal button electrodes in horizontal welll

从图4可以看出，1，2，4，5，6和8号钮扣电极测井响应与传统侧向类测井在直井中的测井响应类似，当仪器靠近地层界面处时，由于电荷的累积，具有“犄角”现象，离开地层界面时也是如此；仪器在地层上下界面处的测井响应不对称。相比而言，3号和7号钮扣电极与地层界面相垂直，仪器接近界面过程中产生的“犄角”现象不明显。8个方位钮扣电极在接近界面时的电阻率变化不同，可以利用仪器不同方位钮扣电极靠近地层界面时的电阻率差异来探测地层界面。

将上述计算模型简化为两层水平地层，考察仪器对界面的识别能力。界面之上地层电阻率Rt1为1 Ω·m，界面之下地层电阻率Rt2分别为1，10，100和1 000 Ω·m。仪器位于界面之下，考察仪器逐渐向界面靠近过程中的响应特性。根据方位性电阻率测量差异，定义仪器边界探测参数DE为：

式中：R0为靠近地层界面处钮扣电极测量视电阻率，相当于1号钮扣电极测量视电阻率，Ω·m；R180为远离地层界面处钮扣电极测量视电阻率，相当于5号钮扣电极测量视电阻率，Ω·m。

图5所示为仪器地层边界探测能力。由图5可知，地层电阻率对比度为1时，相当于均匀地层，DE为0；当地层电阻率对比度大于等于10以后，随着仪器逐渐靠近地层界面，DE逐渐增大，且不同地层电阻率对比度对DE的影响较小，说明利用不同方位钮扣电极测得的视电阻率可以预测仪器与地层界面的距离。

图 5 仪器地层边界探测能力Fig.5 Formation boundary detection capability of the instrument

2.2 斜井测井响应数值模拟结果

钻井过程中，钻头从垂直层段进入水平层段之前需要进行造斜，随钻测井在斜井中具有重要的作用。为此，建立了斜井两层地层模型（见图6），地层界面之上为低阻层，电阻率Rt1为1 Ω·m，地层界面之下为高阻层，其电阻率Rt2为1 000 Ω·m。仪器从地层上界面逐渐向下钻进，钮扣电极与界面沿着井轴方向的距离定义为MD，考察仪器对界面的响应特性。仪器在界面之上定义MD为正，仪器在界面下时定义MD为负，仪器与地层界面的夹角为θ。

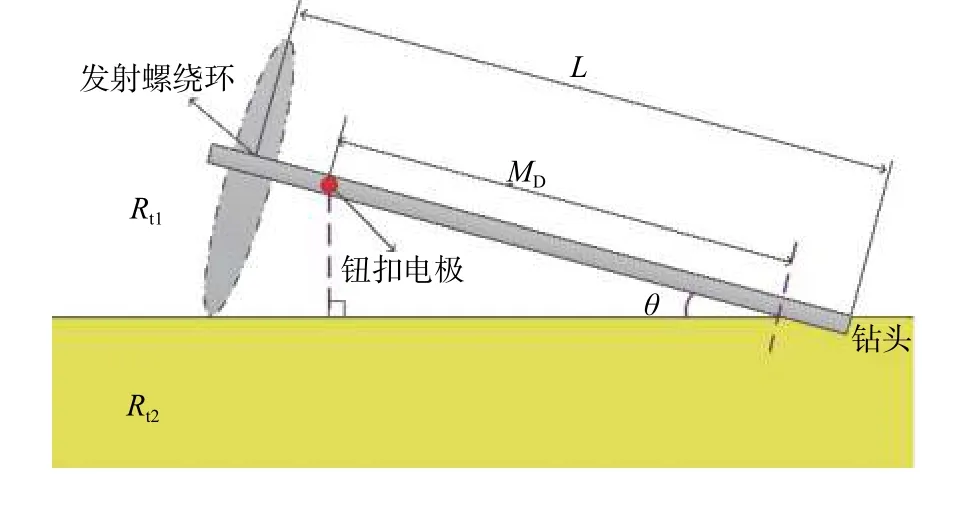
图 6 斜井地层界面模型Fig.6 Formation boundary model for deviated well

利用图6所示模型和对应的参数进行有限元数值模拟，可得到钮扣电极B1和B2在测量深度上的测井响应曲线，其中B1的测井响应曲线如图7所示（图7中，距地层界面最近钮扣电极和最远钮扣电极在靠近地层界面时获得测井曲线的犄角沿测量深度的距离定义为犄角间距离Dmax）。从图7可以看出，仪器与地面界面夹角θ为5°时，Dmax最大，二者在靠近地层界面形成的2个犄角深度相差约2.00 m；随着夹角θ增大，Dmax越来越小，当夹角为45°时，不同方位钮扣电极测量的视电阻率曲线几乎重合，此时不同方位钮扣电极距地层界面的距离增大，导致不同方位钮扣电极测量视电阻率的差异很小。因此可以通过绘制不同方位钮扣电极的视电阻率曲线，来判定仪器和地层之间夹角的大小。

为了验证不同地层电阻率对比度下该结论的适用性，设定图6模型中Rt1为1 Ω·m不变，Rt2分别为10，100和1 000 Ω·m，即上下地层电阻率对比度Rt2/Rt1分别为10，100和1 000，仪器与地层夹角θ为5°，模拟得到不同电阻率对比度下仪器视电阻率与地层界面距离MD的关系曲线（见图8）。从图8可以看出，上下地层电阻率对比度不同时，1号和5号钮扣电极获得犄角的位置均十分接近，即地层电阻率对比度对Dmax的影响较小，说明在不同地层情况下均可预测仪器与地层界面的夹角。

由以上研究可知，利用不同方位钮扣电极的测井曲线间的差异，可以计算仪器与地层界面的距离和仪器与地层界面的夹角，结合仪器的地理方位测量系统，可实现井眼轨迹的控制。

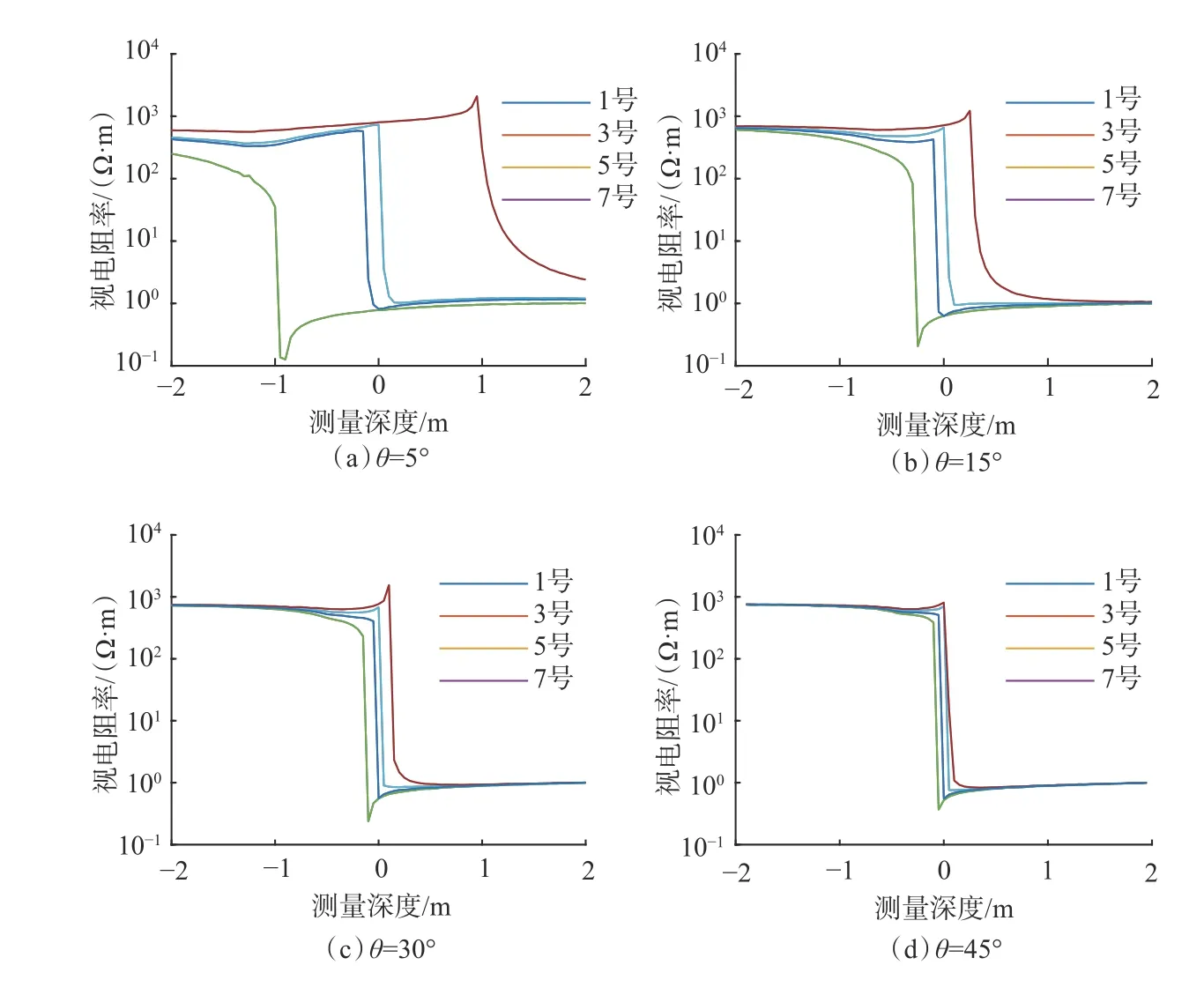
图 7 仪器与地层界面夹角不同时B1的测井响应特征Fig.7 Logging response characteristics of B1 at different angles between instrument and formation interface

图 8 不同电阻率对比度下仪器视电阻率与地层界面距离MD的关系Fig. 8 Relationship between instrument apparent resistivity and formation interfacial distance MD at different resistivity contrasts

3 地层界面识别模型

3.1 水平井中仪器与地层界面距离计算模型

由图5中仪器边界参数参数DE和仪器与地层界面距离Z的关系可知，利用随钻电阻率成像测井的方位性差异可以判断仪器与地层界面平行时二者的距离，对应的实际钻井情况就是水平井中的水平界面。以钮扣电极B1为例，绘制图5中上下地层电阻率对比度Rt2/Rt1分别为10，100和1 000时的边界探测参数DE与地层界面距离Z的关系曲线（见图9）。

图 9 边界探测参数与地层界面距离的关系曲线Fig.9 Relationship curve between boundary detection parameters and formation interfacial distance

对图9进行拟合，可以看出二者呈幂指数关系：

由式（8）可以得仪器与地层界面距离的计算模型：

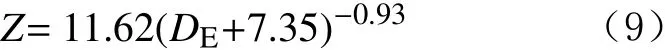
利用式（9），可以计算得到地层对比度Rt2/Rt1为10时仪器与地层界面距离与模型理论值之间的误差（见表1）。从表1可以看出，二者的相对误差较小，最大相对误差小于10%，说明利用模型计算出的地层界面距离可判断地层界面。同时，地层界面距离大于1.00 m时，虽然理论计算误差很小，但由于DE随着Z增大变化较小，导致模型计算结果的误差可能会增大，综合考虑，该模型适合检测地层界面与仪器距离小于1.00 m的情形。理论研究认为，利用该模型可及时判断地层界面的存在，降低了井眼轨迹与储层位置的相对不确定性，有助于现场实时调整井眼轨迹，使仪器处于地层中的最佳位置。

表 1 地层界面距离相对误差分析Table 1 Analysis of relative error for formation interfacial distance

3.2 斜井中仪器与地层界面夹角计算模型

根据图7中不同夹角θ下钮扣电极1和钮扣电极3测井曲线的犄角间距离，绘制Dmax与不同夹角θ的关系曲线（见图10）。从图10可以看出，随着夹角θ增大，Dmax依次减小，二者呈幂指数关系。夹角为2.5°时，模拟计算出的Dmax可达3.75 m；而夹角大于20°时，Dmax较小，且随着夹角增大变化较小。

图 10 仪器与地层夹角和犄角间距离的关系曲线Fig.10 Relationship curve of angle between instrument and formation and distance between horns

对图10中的模拟数据进行拟合，可以得到：

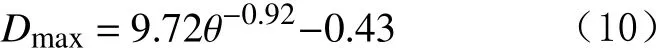
由式（10）可以得地层界面与仪器夹角的计算模型：

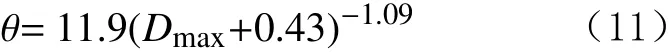
利用上述计算模型计算夹角与模型理论夹角之间的误差，结果见表2。从表2可以看出，夹角小于20°时，模型计算得到的夹角与理论模型十分接近，大部分相对误差小于3.10%；而夹角大于20°时，计算误差较大。从图10还可以看出，夹角过大时，得到的Dmax很小，且相差不大，此时用该模型计算夹角不合适，因此，该模型适用于夹角小于20°的情形。需要注意的是，虽然该模型是在斜井中得到，但是该模型适用于所有仪器与地层界面斜交的情况；同时，由于钮扣电极距离钻头仍有一定距离，实时计算得到的仪器与地层夹角是在钻头即将穿过或者已经穿过地层的情况下获得的，因此，仪器与地层界面夹角的计算模型适用于钻后测井资料的二次解释，但这一特点也限制了该模型的适用范围。

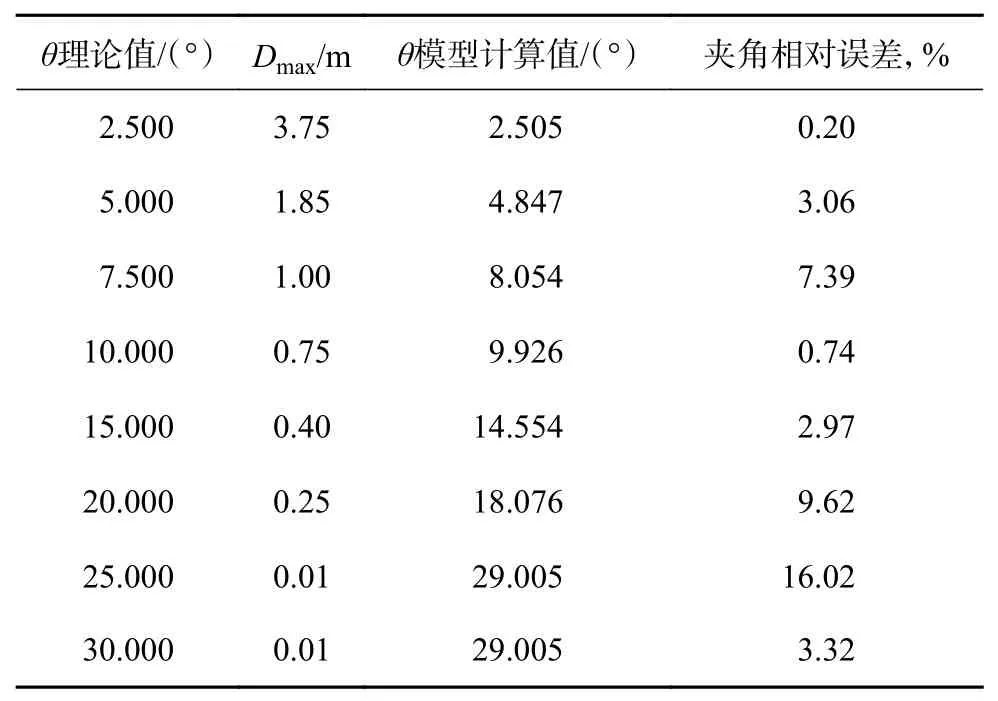
表 2 模型夹角相对误差分析Table 2 Analysis of relative error of the model angle

4 结论与建议

1）建立了随钻电阻率成像测井三维有限元数值模拟模型，模拟了仪器在水平井和斜井中的测井响应规律，仪器在地层界面处不同方位钮扣电极测得的电阻率差异较为明显，利用其可定量评价仪器与地层界面的距离和仪器与地层界面的夹角。

2）基于正演结果，建立了随钻电阻率成像测井仪器地层界面解释模型，表明随钻电阻率成像测井仪器具有一定的地质导向功能，并给出了利用模型计算地层界面距离和仪器与地层界面夹角的适用范围。

3）建立的解释模型和研究结果是在数值模拟基础上得到的，建议今后利用实际随钻测井资料进行进一步验证，并改进模型。