基于云模型的混凝土坝变形安全评价方法研究
刘可心,李艳玲,赵尹利,卢 祥,朱斯杨
(四川大学水利水电学院 水力学与山区河流开发保护国家重点实验室,成都 610065)
以监测资料为基础的大坝安全评价是保障大坝安全的主要途径之一,目前在划分等级时往往需要找到指标包含信息的极限状态值作为风险等级评语集的边界,这个极限状态值一般是规范规定值和设计标准值[1]。然而,对于混凝土坝的变形监测效应量,并没有相关的规范和设计规定出上下限[2]。因此,往往对其利用概率模型,或根据工程经验构造隶属函数,拟定出等级划分的阈值,带入评价期内获得指标等级[3,4]。可以看出,利用此方法构造隶属函数计算等级阈值时主观性很强,忽略了隐藏在数据背后的分布规律,不能准确描述监测量母体空间的极限状况;同时,由于监测仪器、人员、环境量等不可控因素,通常会导致不可避免的误差,造成监测信息的不确定性。谷艳昌[5]等将风险管理与混凝土坝变形预警相结合,使模型不仅满足工程安全需要,同时体现大坝风险要求;李丹[6]等将ACO-SVR法应用于混凝土坝变形监测,提高了监测模型的泛化能力;张海龙[7]等提出了改进PSO-ELM算法的混凝土坝变形非线性监测模型,克服了取值随机性带来的误差。这些方法促进了我国混凝土坝变形安全监测评价的发展,但总的来说,这些方法缺乏对模糊性和随机性的考虑,其评价结果的准确性还有待提高。
云模型是我国李德毅院士在传统模糊集理论和概率统计理论的基础上提出的专门研究复合不确定性的现代数学理论,可较好地描述变量的随机性和模糊性,实现定性概念和定量数值之间的不确定性转换,同时考虑监测量所在母体空间的整体分布类型[8]。因此,本文将充分利用云模型的优势,对混凝土坝变形安全评估中监测序列的等级阈值进行设置。
1 基本理论
1.1 云模型理论[8]
设U是一个用精确数值表示的定量论域,F是U上的定性概念。若定量值x∈U,且x是定性概念F的一次随机实现,x对U的确定度CF(x)∈[0,1]是一个具有稳定倾向性的随机数,即:
CF(x):U→[0,1] ∀x∈X(X⊆U)x→CF(x)
(1)
则x在论域U上的分布称为云,每一个x称为一个云滴。
云模型具体的实现方式有多种,其中最基本、最典型、应用范围最广泛的是正态云模型,如图1所示。其中,Ex为变量实际状态的估计量,在Ex周围存在大小为En的离散程度,同时在En周围存在大小为He的离散程度,两者的离散状态均服从正态分布。

图1 云数字特征图Fig.1 Cloud digital feature map
云模型中定性概念与定量数值之间的转换通过云发生器实现。如图2所示,正向云发生器能够实现从定性概念到定量数值的映射;逆向云发生器能够实现从定量数值到定性概念的转换。
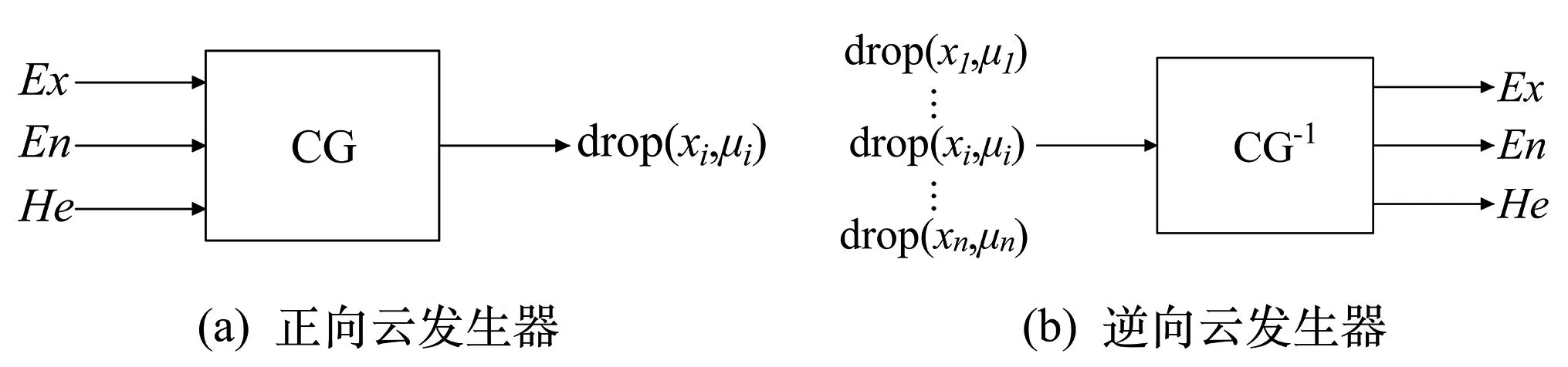
图2 云发生器Fig.2 Cloud generator
1.2 M估计量
正态云模型建立在正态分布的基础之上,参数估计比正态分布更加复杂。当样本数据服从正态分布时使用云模型计算,参数估计贴合监测量的实际情况,适用性良好。反之则导致划分的等级偏离监测项目的正常极限状态。在混凝土坝变形监测项目中,波动型测点的监测序列偏离正态分布明显,对云模型的适应性较差,因此,为反映波动型测点剔除外界影响后的真实均值μ和标准差σ,引入稳健M估计量,以M估计量和基于M估计量的尺度估计量构建3σ准则对序列的波动数据进行筛除[11],计算公式如下:
(2)
MAD=mediani{|xi-M|}
(3)
式中:Tn为基于权重函数ω的加权均值;xi为样本序列观测量;n为序列样本个数;c为细调常数;M为样本序列中位数;median(·)函数返回给定序列的中位数;Sn是辅助尺度估计,通常取中位数离差MAD,即各个观测量到中位数M的距离的中位数。
基于M估计量的尺度估计量为:
(4)
式中:ψ函数为目标函数的导函数;ψ′函数为ψ函数的导函数。
则基于稳健估计量的3σ准则表示为:
Tn-3ST≤Xi≤Tn+3ST
(5)
在确定出模型的Ex和En后,将外界环境对数据序列的影响反映在超熵值He上,即在计算超熵He时考虑筛除波动点前的数据。
2 基于云模型的混凝土坝变形安全评价方法
研究表明[10-12],混凝土坝变形监测序列隶属于N~(μ,σ2)的正态模型。然而,由于监测仪器、监测环境等对监测水平的影响,监测序列并不完全服从N~(μ,σ2)正态模型,可能会发生一定的偏差。同时,这样的偏差也存在一定的规律性,服从正态分布[13]。对于监测量,不仅要考虑数据本身符合正态分布的波动,也要考虑偏离正态分布的程度,因此,引入云模型确定指标评价等级阈值。
2.1 基本思路
在基于云模型的混凝土坝变形安全评价模型中,识别目标为混凝土坝变形安全状态,识别对象为具体的大坝,基本算法为云发生器,以监测测点的数据样本作为评价指标,评价测点的监测序列,并依托《水电站大坝运行安全评价导则》(DL/T 5313-2014)[14],得出混凝土坝变形诊断结果。评价流程如图3所示。
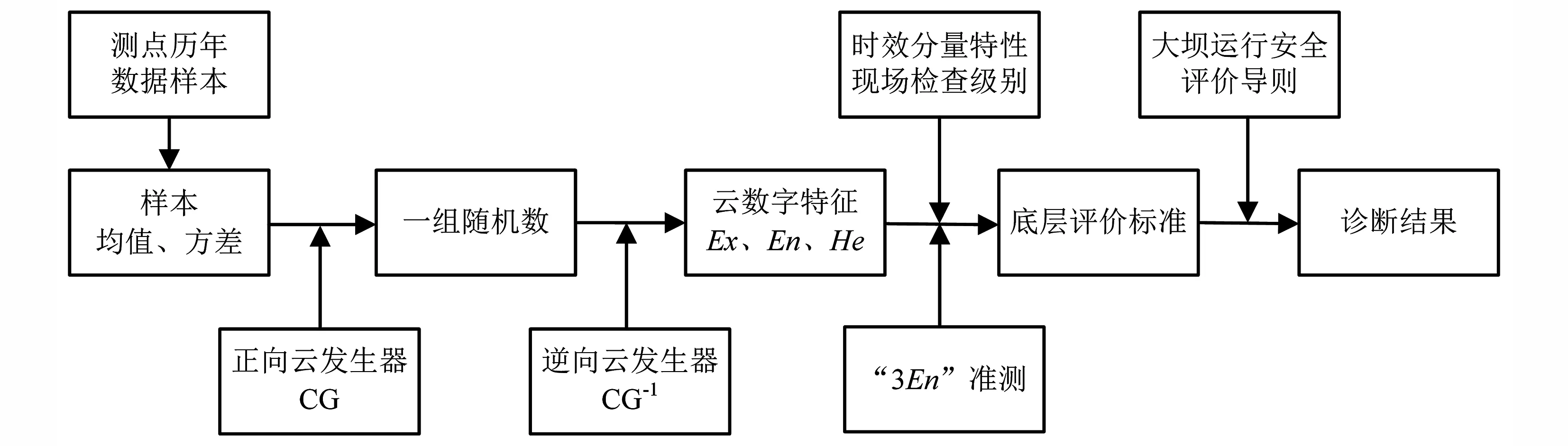
图3 评价流程Fig.3 The process of evaluation
2.2 等级划分及阈值设置
对于云模型,云滴可以分为4类元素:骨干元素、基本元素、外围元素以及弱外围元素。其中基本元素、外围元素与弱外围元素的贡献和,即位于区间[Ex-3En,Ex+3En]的元素占总贡献的99.73%,这被称为云模型的“3En准则”[8]。
如图5所示,当He=0时,云滴分布在一条正态分布曲线上,此时只考虑了数据分布特点,未考虑数据分布的不确定性;当He>0时,云滴分布呈现离散状态,根据“3En准则”可知
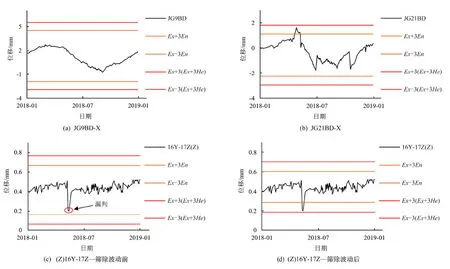
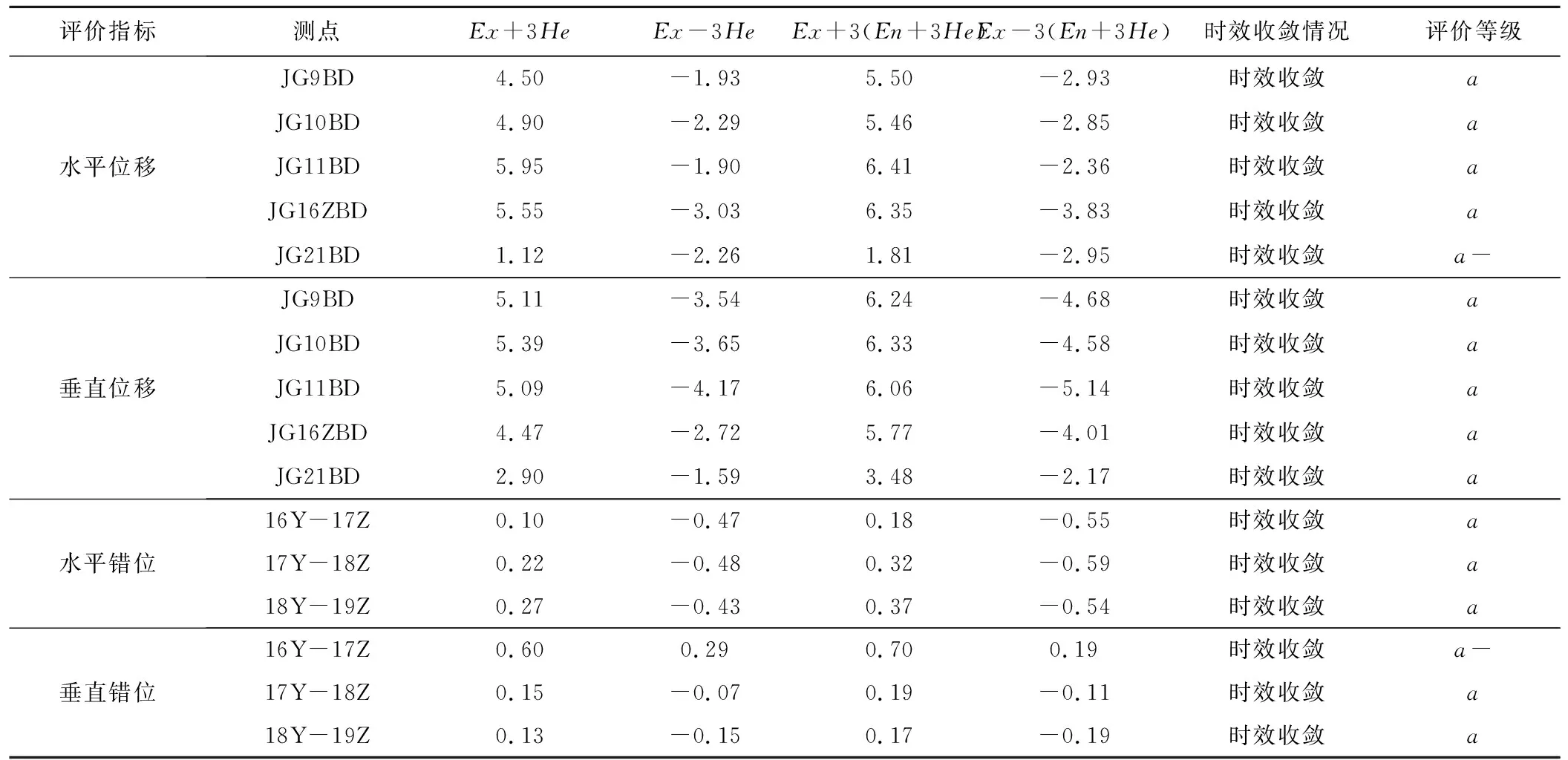
P{En-3He (6) 图4 云滴元素对云模型的贡献率Fig.4 Contribution rate of cloud drop elements to cloud model 图5 云模型轮廓线Fig.5 Cloud model outline 云滴两侧存在内外两条轮廓线。轮廓线是考虑了区间本身不确定性服从正态分布的包络线,99.7%云滴都分布在轮廓线以内,轮廓线公式分别为: (7) (8) 在拟定评价等级时,基于云模型的“3En准则”,使用云期望曲线和轮廓线制定等级阈值: (1)当评价期监测序列的所有监测值均落入Ex∓3En以内区域或时,认定数据序列对N~(μ,σ2)分布的贡献率较大,数据序列正常; (2)当评价期监测序列有监测值落入Ex∓3En以外,Ex∓3(En+3He)以内区域时,认定监测序列出现了一定的波动,但属于正常现象; (3)当评价期监测序列有监测值落入Ex∓3(En+3He)以外区域时,则认定数据序列对N~(μ,σ2)分布的贡献率很小,偏离了正常分布,说明该监测时序发生异常。 评价标准及等级划分情况如表1所示。 表1 评价标准及等级划分Tab.1 Evaluation standard and classification 参照《水电站大坝运行安全评价导则》规定的分级准则将指标评判值和分等分级标准进行对比,确定出混凝土坝变形各监测测点的评价等级,并依据各测点的评判等级以及导则中多层次递归评价原则得出混凝土坝变形安全诊断结果。 某混凝土重力坝最大坝高82 m,布置了较齐全的变形监测设施,取得了大量的实测资料。如图6所示,该重力坝在坝顶布设了真空激光系统,测点编号从左岸至右岸依次为JG5BD~JG23YBD,溢流坝段及部分坝段布设两个测点。在溢流坝段由相邻两坝段间真空激光测点进行位错监测,如16坝段与17坝段位错计为16Y-17Z。结合图3所构建的评价流程,采用本文提出的基于云模型的混凝土坝变形安全评价方法,对该混凝土坝的变形性态进行评价。 图6 混凝土坝平面布置Fig.6 Layout plan of the concrete dam 计算出该混凝土坝底层评价指标中典型测点样本的中心值Ex和熵值En,超熵He根据经验取为熵值En的1/10;随后采用正向云发生器生成3 000个云滴,利用逆向云发生器将所生成云滴得出各监测测点的等级划分。 此处以规律型测点JG9BD-X、台阶型测点JG21BD-X以及波动型测点(Z)16Y-17Z为例。从图7(b)可以看出,测点JG21BD-X在2015年12月处前后有明显的台阶,考虑台阶前后数据差异较大,因此采用台阶后数据进行云模型等级划分的计算;从图7(c)可以看出,测点(Z)16Y-17Z在2014年08月至2015年06月出现波动。 图7 监测序列过程线Fig.7 Process lines of monitoring sequences 测点JG9BD-X、JG21BD-X及(Z)16Y-17Z的等级阈值如表2所示。由图8(c)和图8(d)可以明显得出,波动型数据在筛除波动前无法准确判断出监测序列的异常情况。现场检查情况正常,各测点均时效收敛,因此得出测点JG13BD-X为a级,测点JG21BD-X与(Z)16Y-17Z为a-级。 表2 监测序列等级阈值和分级Tab.2 Monitoring sequences level threshold and classification 图8 监测序列评价过程线Fig.8 Evaluation process line of monitoring sequences 结合该混凝土坝上、下游混凝土坝面的巡视检查和水下检测情况,可知该大坝上游坝面混凝土结构表观完整情况整体良好,未发现明显混凝土损伤现象,现场检查结果为正常,所有测点均时效收敛。根据垂直和水平变形指标的评价标准及等级划分,垂直变形指标的评价等级为a级,水平变形指标的评价等级为a-级。根据该工程2018年的日常和年度巡检信息,相邻坝段之间未发现错位现象,止水完好,根据相邻坝段错位指标的评价标准及等级划分,得出相邻坝段错位指标的评价等级为a-级。典型测点评价等级如表3所示。 表3 典型测点评价等级Tab.3 Evaluation grades of measuring points 根据《2018年某水电站大坝安全年度详查报告》:2018年度坝顶激光水平位移年变幅在2.34~4.69 mm之间,最大年变幅出现在16号坝段(JG16ZBD测点),最小年变幅出现在9号坝段(JG9BD);垂直位移年变幅在2.49~4.35 mm之间,最大年变幅出现在11号坝段(JG11BD测点),最小年变幅出现在21号坝段(JG21BD);水平错位年变幅在-0.06~0.18 mm,最大年变幅出现在16、17号坝段(16Y-17Z),最小年变幅出现在18、19号坝段(18Y-19Z);垂直错位年变幅0.09~0.14 mm,最大年变幅出现在16、17号坝段(16Y-17Z),最小年变幅出现在18、19号坝段(18Y-19Z)。大坝水平位移 、垂直位移变化规律合理,测值在合理的变化范围内;相邻坝段错位未出现明显的异常,大坝处于正常工作状况。因此,本文采用的基于云模型的混凝土坝变形安全评价方法得出的评价结论与传统监测资料分析的结论相一致,说明本文提出的方法是合理、可靠的,同时考虑了监测序列的总体分布情况和由于外界因素导致的监测数据时空上的不确定性,因而比常规监测资料分析给出的信息更全面,适用性更强。 本文将云模型理论与传统的多层次递归评价相结合,提出了基于云模型的混凝土坝变形安全评价模型,同时通过引入M估计量提高了模型对于波动型数据的实用性,为混凝土坝变形安全评价提供了一种高效合理的方法,并应用于具体工程,结果表明。 (1)在确定监测序列指标评价等级阈值时,本文提出的评价模型同时考虑了数据本身符合正态分布的波动以及偏离正态分布的程度,因而评价过程能更有效地反映影响混凝土坝健康状态的不确定性因素,评价结果能更合理地反映混凝土坝的实际健康状态。 (2)评价模型对于规律型数据、平稳型数据以及采用稳健M估计量处理后的波动型数据和选取台阶后序列的台阶型数据均有较高的精度。 (3)由“3En准则”得出的等级划分标准对某混凝土坝变形性态进行了评价,并根据评价模型得出该混凝土坝的变形性态为a-级正常状态,与大坝实际情况一致,故采用基于云模型的混凝土坝安全评价方法是合理可行的。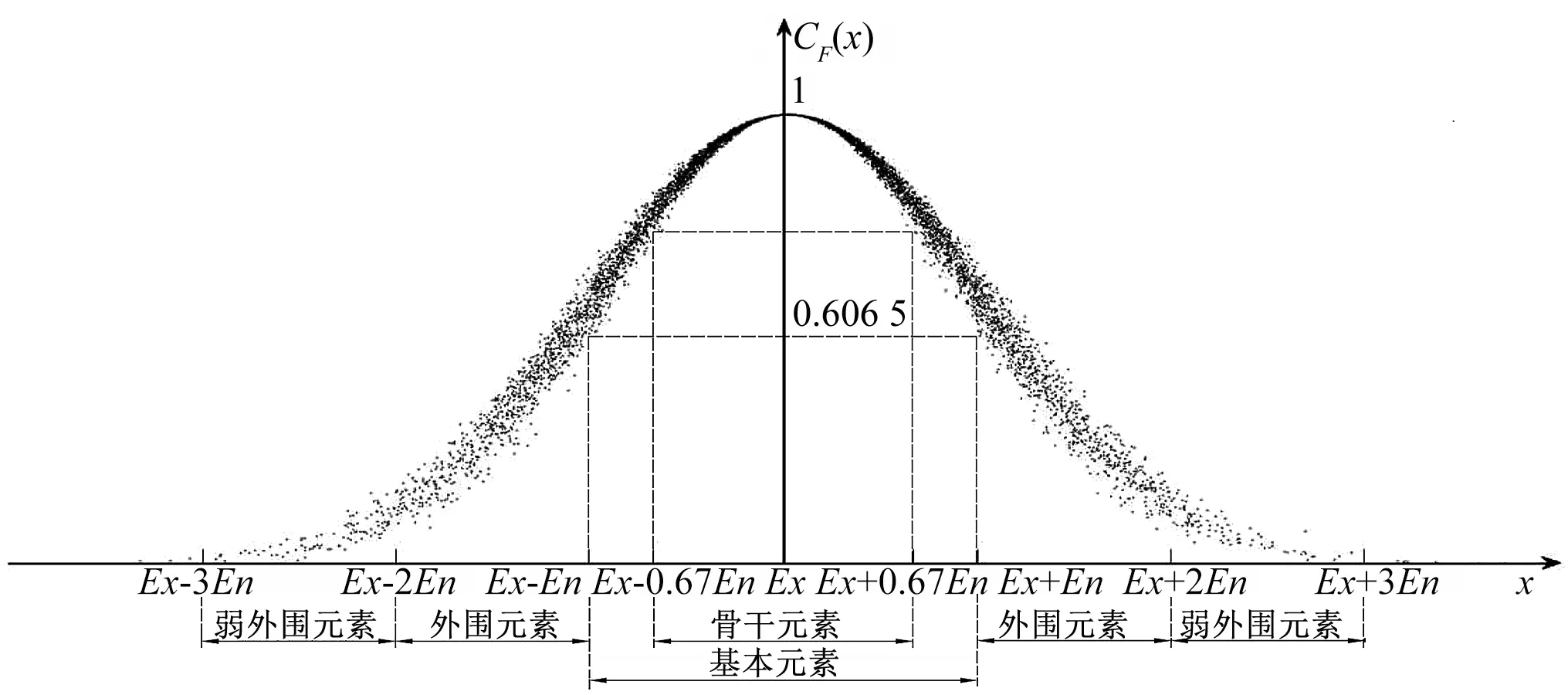


3 案例分析
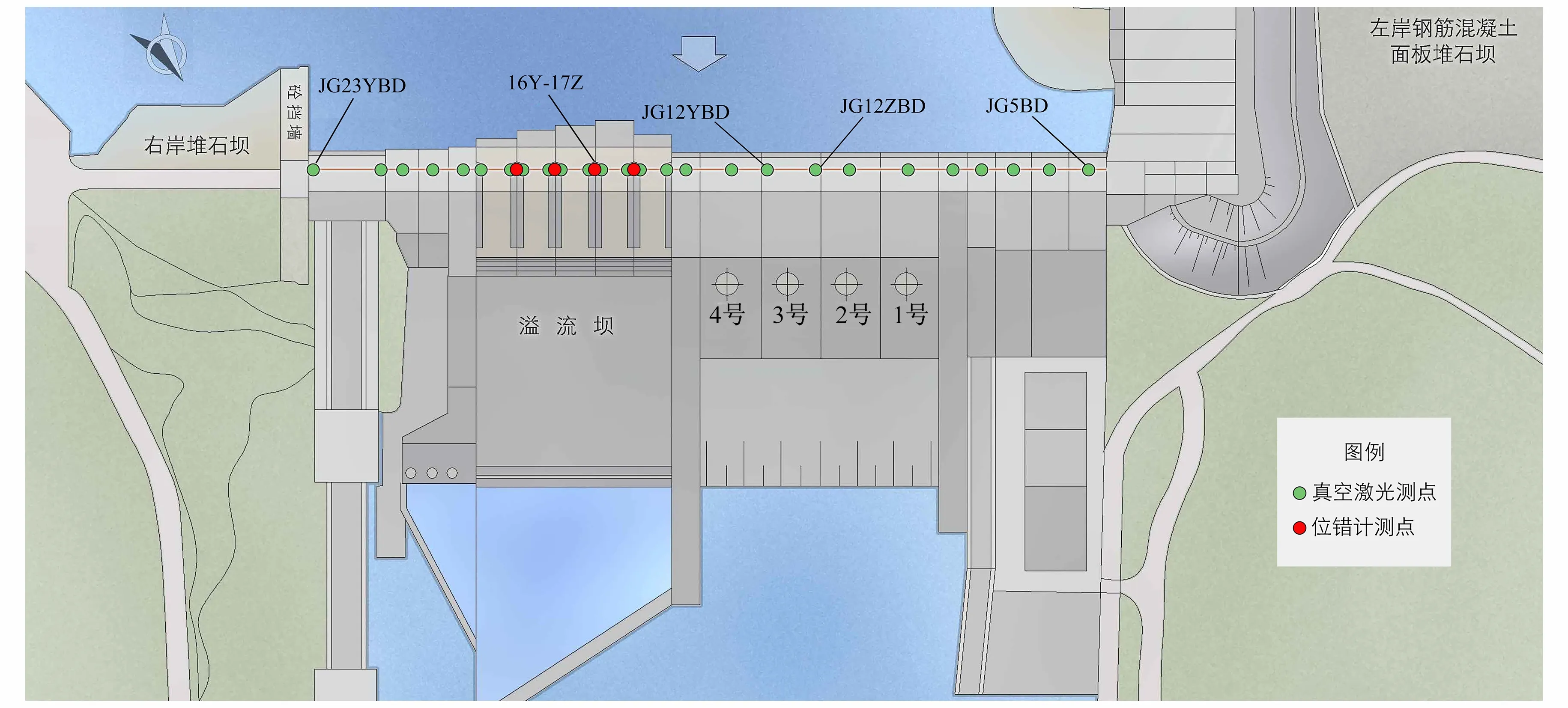
3.1 评价指标等级划分计算


3.2 变形性态评价
3.3 诊断结果验证
4 结 论
——以徐州高层小区为例

