基于多目标遗传算法的施工班组调配优化研究

胡艾霖，吴鑫淼，郄志红，郑一宁

(河北农业大学城乡建设学院，河北 保定 071001)

0 引 言

大型工程项目施工是一项复杂的系统工程，施工组织管理直接关系到工程的进度、质量和、成本和安全性，而施工进度与施工条件，施工技术水平，资源投入、施工人员配置管理等因素有很大的联系[1]。目前国内外有专家学者对于施工进度方面的研究大多注重于工期优化或考虑工期、成本和质量的多目标综合优化，例如Badu和Suresh建立了工期-成本-质量3个目标合一的线性规划的数学模型[2,3]；朱光熙、孙锡衡等将仿真方法应用于龙滩面板堆石坝[4]；钟登华等将仿真技术和数据库技术应用于大型土石坝、堆石坝施工模拟与进度计划优化[5,6]；Heimerl和Kolisch考虑到工作效率对活动时间的影响，并在多项目环境下建立数学模型运用优化软件求解[7]；张立忠等人以拉脊山隧道工程为例，分析高原缺氧对人员与机械的影响，根据施工任务逐步增加施工人员机电设备配置，加快施工进度[8]。金红，徐璐君考虑在建筑项目中施工人员加班时长限制和每个计划阶段的施工人员流动量限制，运用运筹优化软件CPLEX求解，得到最佳人员调度方案[9]。徐世斌[10]在工期固定和工人施工成本相同的情况下建立施工人员均衡优化模型，并运用遗传算法对装修施工人员均衡问题进行求解。

众所周知，施工人员对某项施工作业的经验和熟练程度是影响工作效率和质量的重要因素，定量表达施工人员以及作业班组对某项作业的经验，并将其引入工程施工的人员配置优化中可以有效提高工作效率，提高工程质量，然而从既有研究成果看，综合考虑施工人员(班组)经验和实现工期和施工作业均衡的施工人员配置多目标优化目前尚不多见，本文拟就此问题进行初步探索。

1 基于施工人员经验值的优化模型

1.1 作业人员及班组的施工经验值

不同人员对不同施工工序(作业)的熟悉程度不同，这里以经验值来表示某个人员或班组对某一个工序的工作效率。

设定k表示施工工序的总个数，m表示班组的总个数，n表示每个班组的人数，i表示班组序号，j表示施工工序序号。首先，综合所有人员对这k项工序的熟悉程度，分0～4级，级别越高表示其对此项工序施工效率高，之后将所有施工人员按个人技能熟练程度分为m个班组。每班组的经验值由下式计算：

(1)

式中：每个班组的经验值Ei是班组中个人Epi对第i个工序的经验值Epi的总和除以班组人数n求得，取整数。

对于实际工程，通常不同工序的工程量单位并不相同，在此只取数值，并设置函数C来表示相对工期的长短(并不是实际工期)，如式(2)所示，函数S来表示班组作业时间(并不是实际作业时间)，如式(3)所示。

(2)

式中：Ci为第i个工序的工期，其值等于该工序实际工程量Qzi除以参与施工该工序的所有班组经验值的总和∑Ez；Si为第i个班组实际工作时间的方差；Cij为第i个班组在第j个工序的施工天数；μ为m各班组施工时间的平均值。

1.2 考虑经验值施工班组优化配置模型

1.2.1 目标函数

设共有k个工序m个班组，建立基于经验值的施工人员配置优化模型，目标函数模型如下：

目标1 minC=∑Ci(i=1,2,…,k)

(4)

目标2 minS=∑Si(i=1,2,…,k)

其次，这部小说的结构也具有一定的象征意义。福斯特在写作这部小说时，将隐喻和转喻两种修辞手法糅合于整部小说的结构中，因此，《印度之行》这部小说就具有了双重结构。《印度之行》这部小说结构包括表层结构和深层结构，小说的表层结构是直线型的，这种结构形式能够促使小说情节按照时间顺序发展；小说的深层结构是循环型的，这种结构形式能够深化小说的主题，揭示其主题思想。

(5)

式(4)为工期函数模型，总工期等于关键线路上各工序施工时间的总和，其值越小越优；式(5)为班组作业时间均衡函数，为了尽量避免施工过程中有施工人员空闲的状况，尽量实现各班组作业时间的均衡，其值越小越优。

1.2.2 约束条件

(1)一般实际工程在施工阶段，施工工序必须遵从施工工艺的逻辑顺序，即施工工序的紧前紧后关系，进行施工顺序安排。

(2)在经验值以及工序逻辑一定的情况下，每个工序要求施工人员对于此项工程的熟悉程度有不同的要求，即每项工序的对于施工人员的经验值有最低要求，例如参与施工工序5的施工人员要求经验值3以上，那么经验值为0、1、2的施工人员则不能参与施工。

Eij≥Emin(i=1,2,…,m；j=1,2,…,k)

(6)

式中：Eij为第i组参与第j项工程施工的经验值；Emin为第j项工程要求施工人员经验值的最小值。

2 施工人员配置优化求解的多目标遗传算法

2.1 NSGA-Ⅱ多目标遗传算法的特点

本文采用第二代非支配排序遗传算法(NSGA-Ⅱ)，该算法是在常规多目标遗传算法上的改进，加入了快速非支配算子的设计，使得全局优化问题的非劣解(pareto)能均匀的扩散到整个集域上。并设计个体拥挤度算子，在执行操作时通过对个体所在的层级顺序和拥挤距离进行比较，选取合适的个体组成新的父代种群。

2.2 算法设计

2.2.1 遗传编码及染色体设计

设计染色体由两段构成，即:班组基因段和工序基因段，班组基因采用二进制编码，如图1(a)所示，假设共有9个工序，基因位从左到右分别代表相应序号的工序，1表示此班组参加的施工工序，0表示班组未参加该施工工序。工序基因编码规则按照施工顺序将代表此工序的序号依次排列，为自然数编码。假设有k个工序，m个班组，依次将m个班组基因与工序基因连接起来组成完整的染色体。整体染色体编码设计如图1(b)所示。

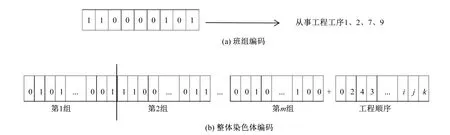
图1 编码设计Fig.1 Code design

2.2.2 pareto解

对于多目标遗传算法，在多个目标互相影响和制约的情况下，基本不会存在多个目标同时达到最优的情况，所以在一定的取舍情况下，使得其中的某个目标达到最优，这样就有了patero最优解。定义如下：

对x*∈X，若存在x∈X(x*≠x)使得f(x)≤f(x*)成立，即不存在x使fi(x)≤fi(x*)对所有的i=1,2，…,n成立，且其中至少一个为严格不等式，则称x*为多目标优化问题的一个最优解(或非劣解)[11]。

2.3 NSGA-Ⅱ多目标遗传算法的实现过程

第一步：随机产生N个满足约束的个体P0组成初始种群PT。

第二步：对初始种群中每个个体进行适应度值计算，并对其进行快速非支配排序以及拥挤度计算，在算法的各个阶段，拥挤度比较算子都引导选择进程朝着均匀分布的Pareto 最优前沿面进行，既保证了个体的优越性，又最大程度的确保了种群的多样性。

第三步：用锦标赛选择法选择父代群体PT，并进行交叉变异等操作产生子代群体QT。

第四步：将父代群体PT与子代群体QT种群合并，根据精英保留策略，再次选择一定的群体，再次进行快速非支配排序。

第五步：若达到一定的迭代次数，输出优化结果，否则，跳转到第二步继续运算。

3 实例应用

3.1 工程简介

某水库枢纽工程中2号副坝为均质土坝，坝顶宽4 m，坝长103 m，坝顶高程48.40 m，上、下游坝坡均为1∶2.75，形状极不规则，且填筑质量较差，经加固后见图2，坝顶高程49.0 m，顶宽6.0 m，坝顶长103 m，坝顶设厚20 cm泥结石路面，上、下游坝坡均为1∶3.0，坝脚设棱体排水，根据渗流计算结果，下游地面高程约为42.20 m，棱体排水顶部高程取44.2 m，上下游边坡分别为1∶1、1∶1.5，并设置反滤层。基础为壤土。黏土斜墙与基础采用黏土齿墙截渗，齿墙底宽3.0 m，深1.0 m，齿墙底部高程41.0 m。

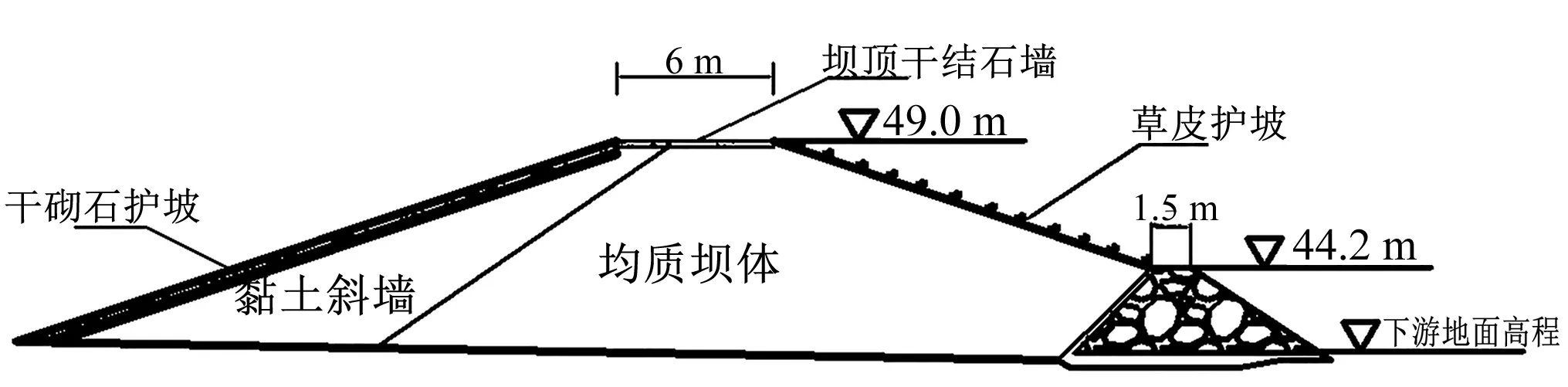
图2 2号副坝除险加固施工图Fig.2 Construction drawing for removal and reinforcement of auxiliary dam

以某水库枢纽工程2号副坝加固工程为例，从2号副坝加固工程中选取部分工程进行施工优化，其中包括：土方开挖(工序1)、坝体填筑(工序2)、干砌石排水棱体(工序3)、斜墙黏土回填(工序4)、草皮护坡(工序5)、干砌石护坡(工序6)、坝顶泥结石道路(工序7)共7个分项工程，在施工阶段，根据施工工艺，不同工序间存在相互关联。各工序之间的逻辑关系如图3所示，从节点1(开始)到节点9(结束)。除了工序之间的逻辑关系要满足条件以外，每个工序对于施工者的经验值要求也不同，只有高于当前设置经验值要求的班组可以参与施工。表1中给出了每个工序对施工班组的经验要求，具体数据见表1各工序工程量，经验要求Emin以及班组经验值Ei。

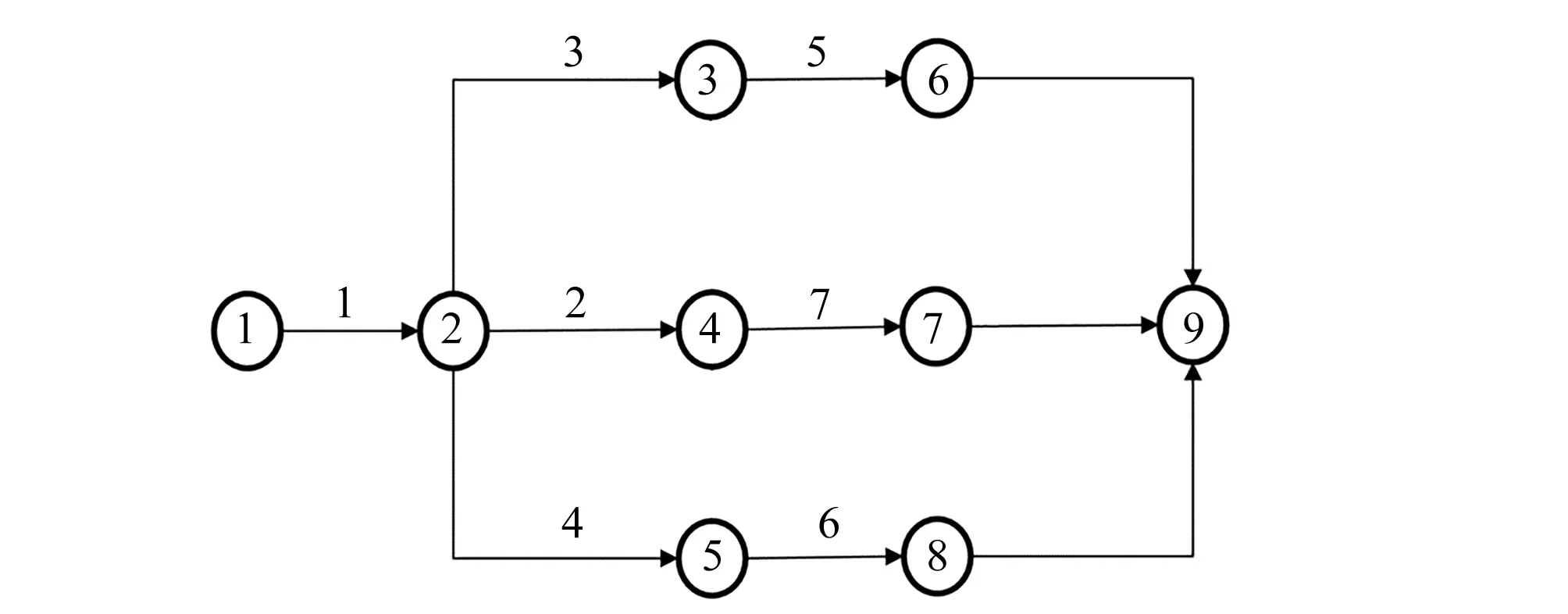
图3 工序逻辑图Fig.3 Process logic diagram

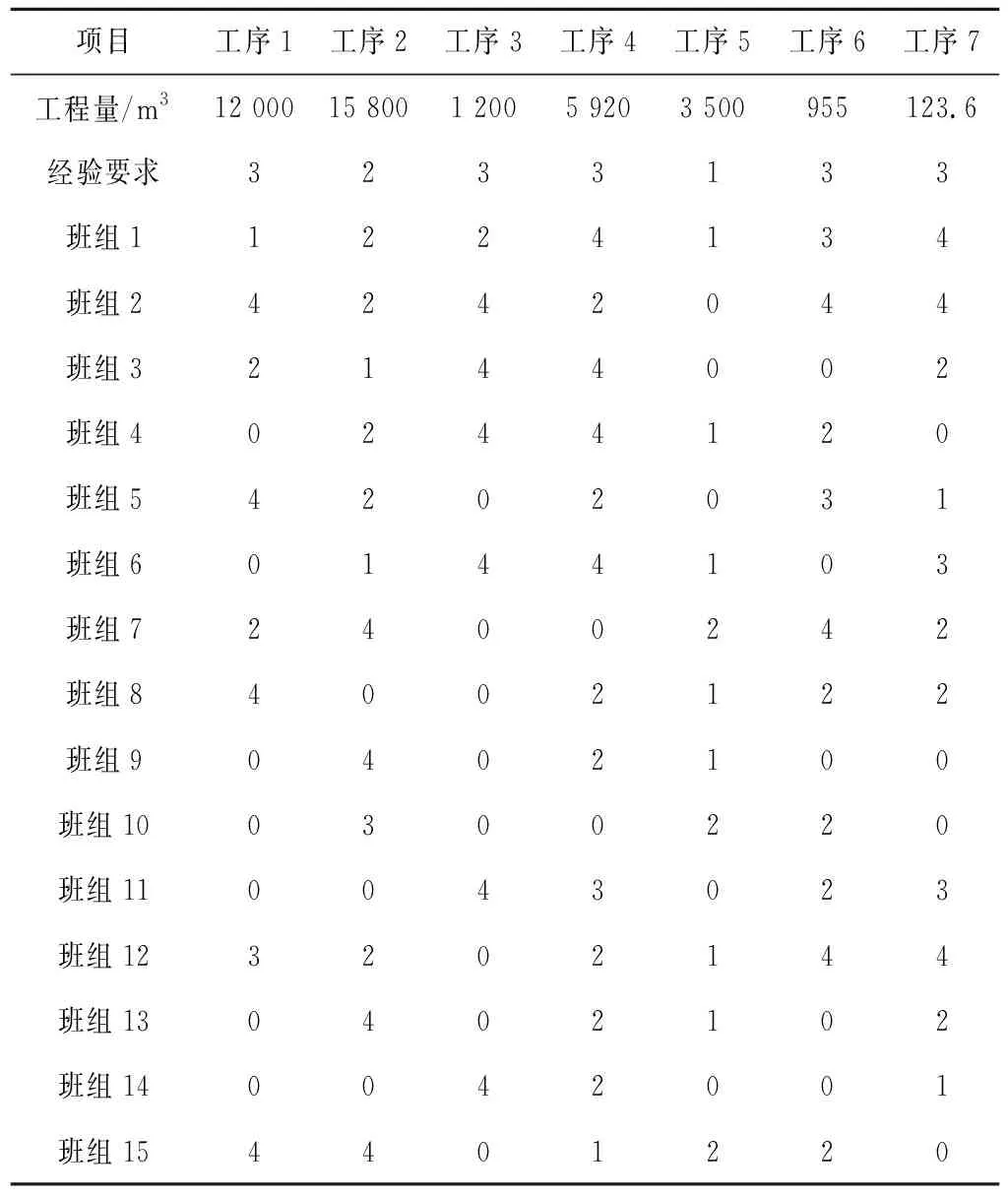
表1 各工序工程量，经验要求以及班组经验值Tab. 1 Engineering quantities, experience requirements and team experience values of each process

3.2 优化过程及结果

优化算法主要考虑人员经验值在施工中人员最优配置问题，根据本文所建立的数学模型，以工程进度长短和施工人员工作时间均衡为目标，应用NSGA-Ⅱ优化算法实现，收敛过程如图4 所示，随着遗传代数的增加，目标函数均呈现单调递减的趋势，具有较好的收敛效果，目标1大概在180代达到稳定，目标2大概在60代左右达到稳定。

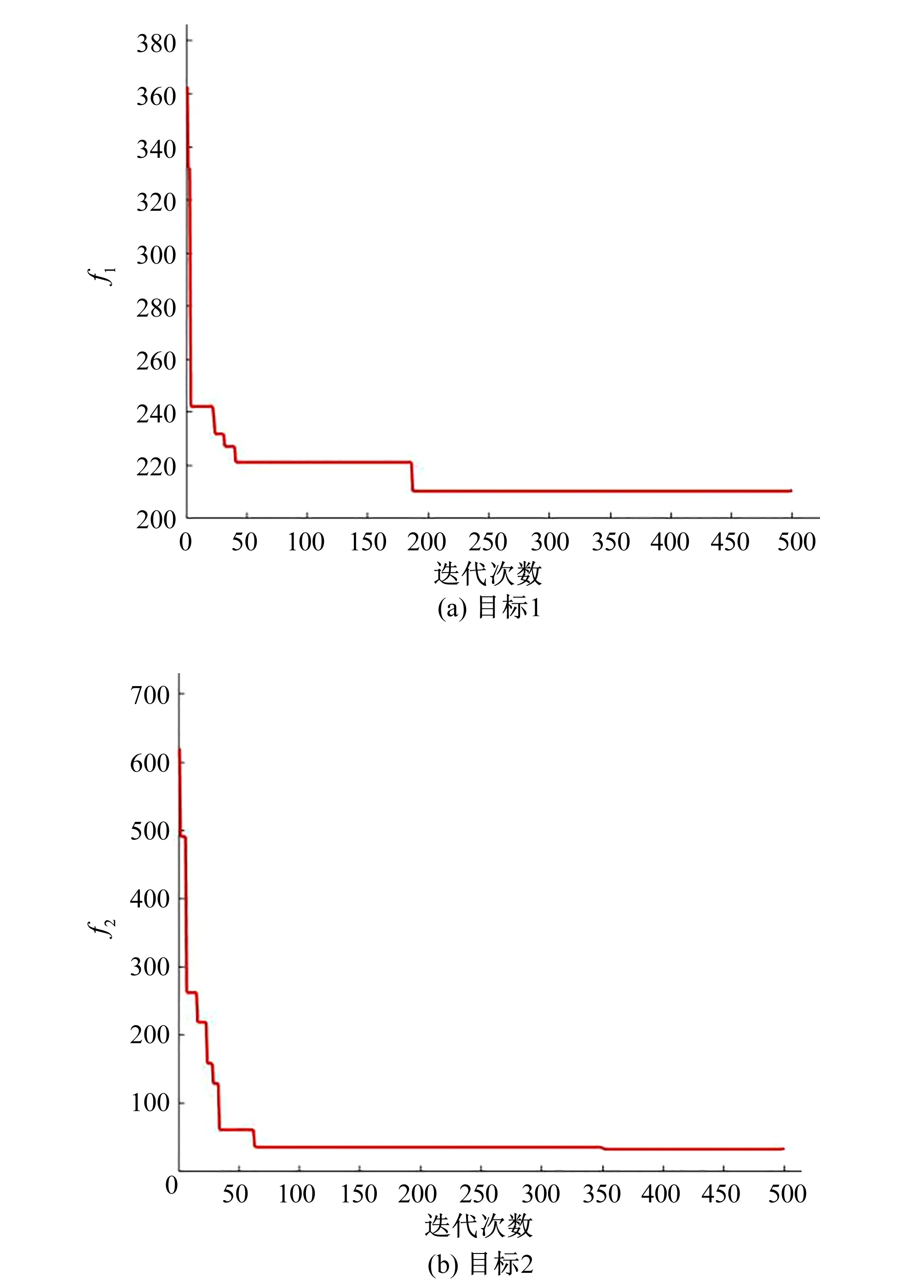
图4 目标函数收敛图Fig.4 Convergence graph of objective function

多目标遗传算法往往会产生多个解，图5是该问题的pareto前沿，图上的所有点均可作为最优解。根据施工方案以及实际情况可以选择最合适的解。

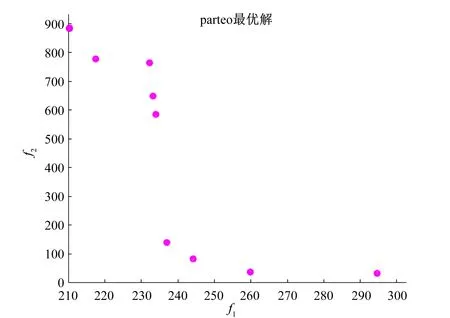
图5 pareto前沿Fig.5 Pareto frontier

以下选取pareto最优解中的一个解，作业调度根据工序逻辑关系为约束条件，最多允许三项工程同时进行。得到最优施工工序为1→2→3→4→6→5→7其中工序2和3，5、6和7同时开始施工，工序2，4存在同时施工阶段，图6为人员安排及作业调度甘特图。

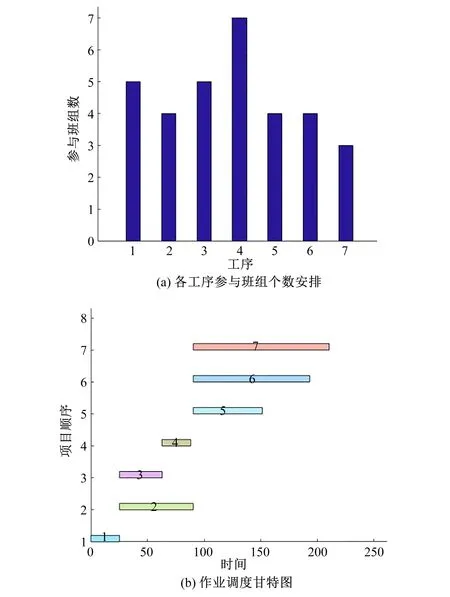
图6 人员安排及作业调度甘特图Fig.6 Gantt chart of staffing and job scheduling

表2为各工序人员调配以及施工时间，工序1施工班组为：2，5，8，12，15；工序2施工班组为：7，9，10，15；工序3施工班组为：2，3，4，6，14；工序4施工班组为：1，2，5，6，8，11，13；工序5施工班组为：4，8，13，15；工序6施工班组为：1，5，7，12；工序7施工班组为：2，6，11。

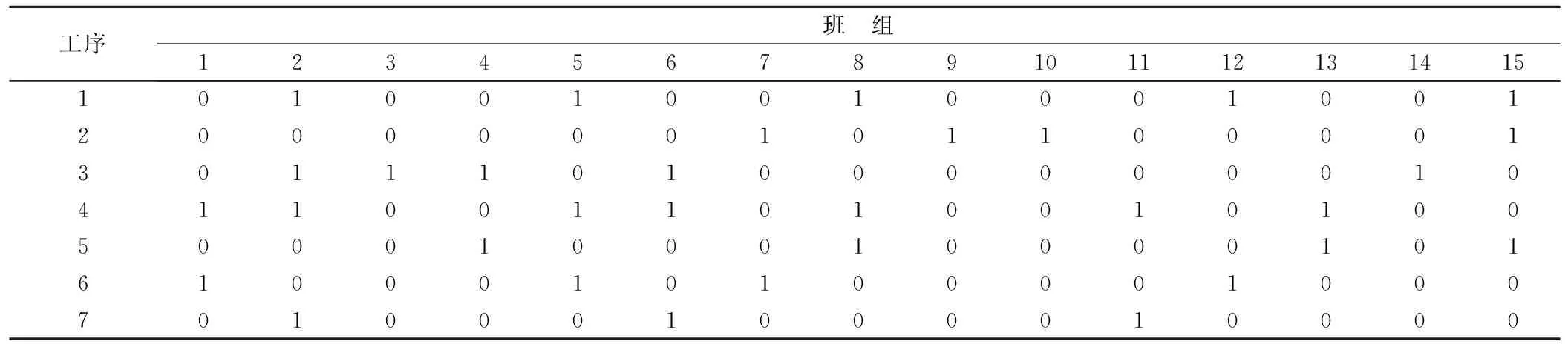
表2 各工序人员调配以及各工序施工时间Tab. 2 Personnel allocation and construction time of each process

4 结 论

通过对施工过程中施工人员配置与施工进度安排关系的研究，本文提出了基于施工人员及班组的概化经验值分析的施工班组调配多目标优化模型，并针对模型的特点，采用非支配排序的多目标遗传算法对模型进行求解。将该模型及优化算法应用于工程实例，验证了模型和方法的可行性。有助于在施工组织决策中合理充分利用人力资源，提高工程建设效率，降低建设成本，提高决策的合理性和科学性。