对旋式轴流泵性能CFD计算分析

孙壮壮，石丽健，汤方平

(扬州大学水利科学与工程学院，江苏 扬州 225000)

0 引 言

对旋式轴流泵具有流量大、扬程高及体积小等特点，被广泛应用于潜艇、滑翔艇等水上航行工具的动力装置。对旋式轴流泵最早于1961年由Ozgur提出，即在普通轴流泵的基础上，增加了一级原叶轮转速方向相反的后置叶轮。普通轴流泵的后置静导叶的作用是消除经叶轮流出水流的速度环量并将部分动能转化为压能，而对旋式轴流泵的后级叶轮在反向旋转的同时，不仅消除了前级叶轮出口的速度环量并回收动能，而且可以在此基础上再次做功，故在某些场合，对旋式轴流泵具有更为优秀的水力性能[1,2]。

近年来，国内外学者对于对旋式轴流泵的展开了研究。王德军等[3]研究了对旋式轴流泵的前、次级叶轮的进出口三角形耦合情况，为对旋式轴流泵的设计提供了指导。黄丹等[4]基于Rayleigh-Plesset空化模型及SST湍流模型，研究了对旋式轴流泵整体及其前、次级叶轮单独的空化性能。黄振杰等[5]应用计算流体力学方法研究了对旋轴流式喷水推进泵进水预旋的产生和发展，解释了小流量工况时其效率下降较快的原因。Furukawa AKINORI等[6]利用试验的方法，研究了对旋式轴流泵的设计方法及水力性能。但总的来说，目前对于对旋式轴流泵的研究仍相对较少。为研究对旋式轴流泵的水力性能及内部流动，应用计算流体力学ANSYS CFX软件对不同工况下对旋式轴流泵进行数值计算，为对旋式轴流泵的设计及应用推广提供指导意义。

1 研究对象及数值计算方法

1.1 计算模型及网格划分

以现有的优秀轴流泵模型叶轮(TJ04-ZL-23)为基础，增加一级的转向相反的次级叶轮，同时后接直导叶组成对旋式轴流泵，如图1所示，次级叶轮及直导叶均为重新设计。该轴流泵模型叶轮的设计参数：设计流量Q=320 L/s，H=3.5 m，转速n=1 450 r/min，叶片数Z=3。次级叶轮的设计参数与首级叶轮相同，采用平面叶栅法进行设计造型。

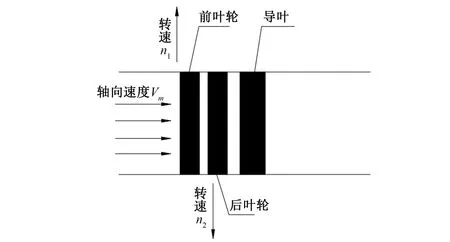
图1 对旋式轴流泵示意图Fig.1 Schematic diagram of counter-rotating axial flow pump

理论上，水流沿垂直方向进入对旋式轴流泵，首级叶轮对水流做功并产生圆周分量速度，再经次级叶轮再次做功并消除首级叶轮出口环量，由于两级叶轮扬程相同，此时水流沿垂直方向流出次级叶轮，且首级叶轮进口速度及次级叶轮出口速度均与轴向速度相同。对旋式两级叶轮叶栅及进出口速度三角形如图2所示(图2中下标F代表首级叶轮参数，下标R代表次级叶轮参数，1代表进口，2代表出口，W为相对速度，V为绝对速度，Vm为轴向速度，U为圆周速度，Γ为环量，t为节距)。

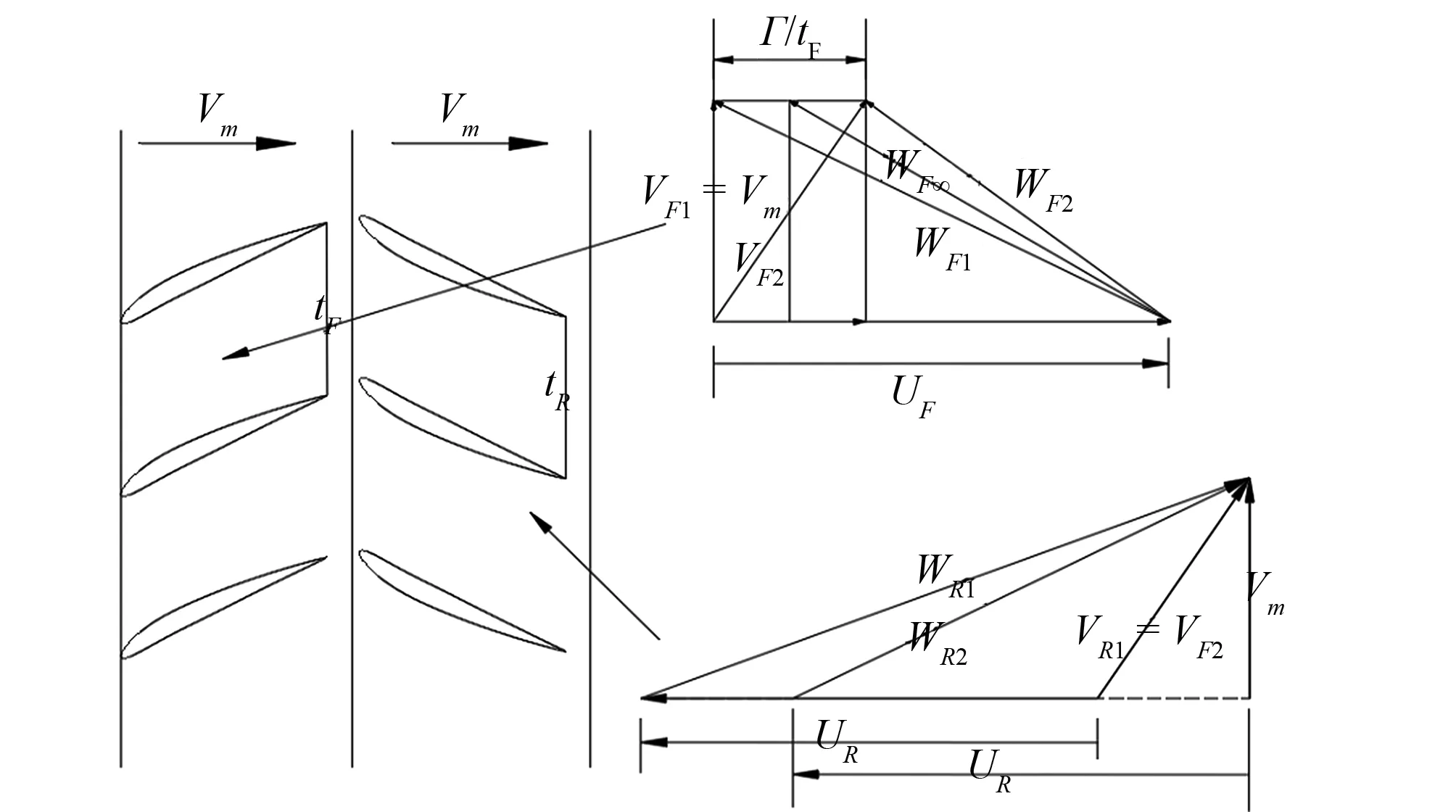
图2 对旋式轴流泵两级叶轮叶栅及进出Fig.2 Two-stage impeller cascade of counter-rotating axial flow pump and inlet and outlet speed triangles

为使数值计算时流动更加充分的发展，对计算域进口段和出口段延伸长度均大于3倍管径，计算区域为进水段、首级叶轮、次级叶轮和出水段。通过PTC Creo 3.0软件对对旋式轴流泵的进口段和出口段进行三维造型，通过Turbogrid对前、次级叶轮造型，如图3所示。

图3 对旋式轴流泵三维模型Fig.3 3D model of counter-rotating axial flow pump

结构化网格是指内部节点具有相同数量的毗邻单位[7]，具有可控性较高、数据结构较简单及收敛较为容易等优点，因此对对旋式轴流泵全流域采用分块结构化网格进行划分，采用的软件为ICEM及Turbogrid，计算网格如图4所示，经检查网格质量均在0.4以上，符合数值模拟要求。

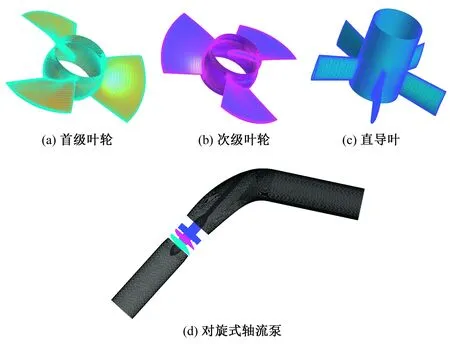
图4 对旋式轴流泵网格划分Fig.4 Meshing of counter-rotating axial flow pump

1.2 湍流模型及边界条件设置

数值计算采用ANSYS-CFX软件进行计算，湍流模型选用SSTk-ω湍流模型[8-10]。基于SST模型的k-ω方程考虑了湍流剪切应力的传输，可以精确的预测流动的开始和负压力梯度条件下流体的分离量。SST模型的最大优点就在于考虑了湍流剪切应力，从而不会对涡流黏度造成过度预测。其传输行为可由包含限制数的涡流黏度方程求得。

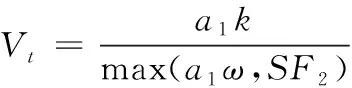
(1)

Vt=μt/ρ

(2)

式中：a1为一个常数；F2为一个混合函数，在近壁处为1，在边界层内部为0，是到壁面距离的函数，对于存在不合适假设的自由剪切流，此数用来约束壁面层的限制数；S为应变率的一个定估算值。

计算中计算区域分为静止域及旋转域，对旋式轴流泵的首级叶轮及次级叶轮段为旋转域，其他区域为静止域。对静止域与旋转域及旋转域与旋转域之间的交界面采用stage，其余交界面采用None交界面，进口断面用总压进口条件，总压设置为101 325 Pa，出口断面采用质量流量出流。参考压力设为0，壁面采用无滑移壁面条件，近壁区采用可伸缩壁面函数，收敛精度设为10-4。

1.3 网格无关性验证

针对研究对象设计流量下的扬程进行网格无关性检测，采取相同的控制方程边界条件，控制网格数量为唯一变量。网格划分时，采用相同的拓扑结构，通过改变节点数目以改变网格的数量，通过计算获得设计流量下扬程随网格数量的变化曲线如图5所示。通常网格越密，计算结果越精确，但这也需要更大的计算资源及时间，由图5可知，当网格增加到675 万个左右时，再增加网格对扬程的影响不大，综合以上考虑，最后确定网格数约680 万个。

图5 网格无关性检测Fig.5 Grid independence detection

2 数值方法验证

为保证南水北调事业的顺利进行，水利部向社会公开征集水泵模型于天津试验台展开同台测试， TJ04-ZL-23轴流泵即为扬州大学送检模型之一，本次试验工作公正规范、科学严谨，具有极高的权威性[11]。利用上述数值计算方法对TJ04-ZL-23轴流泵模型的不同工况下外特性进行预测，数值计算结果与天津试验台试验数据对比如图6所示。通过对比可知，数值模拟结果能够在泵运行工况范围内较好的预测泵外特性。数值计算得到的流量-扬程曲线与试验结果基本重合，而效率略高于试验数据，这主要是因为计算时未考虑摩擦力的影响。额定工况点的扬程、效率相对误差分别为3.1%、2.3%，均小于5%，这也说明数值计算的准确性较高。

图6 数值方法验证Fig.6 Numerical method verification

3 结果与分析

3.1 外特性分析

对旋式轴流泵外特性指标主要包括比转速ns、扬程H及效率η，其计算公式[12]为：

(3)

(4)

(5)

式中：Pin和Pout分别为进出口处总压力；M1和M2为电机轴分别为作用首级叶轮和次级叶轮的力矩；ω为叶轮旋转角速度；n为叶轮转速。

通过软件CFD-POST对计算结果进行处理，得到对旋式轴流泵约在流量320 L/s时的效率最高，这与单级泵的设计流量相近，此时扬程为8.4 m，效率约为82.3%，相比较TJ04-ZL-23，虽然效率有所下降，但对旋式轴流泵的扬程提升了约1倍。由公式(3)可知，此时比转速ns约为600，为进一步评价对旋式轴流泵性能，将其外特性曲线与相同比转速的轴流泵模型对比，如图7所示。通过对比流量-扬程曲线可以发现，小流量工况下，对旋式轴流泵扬程明显大于该轴流泵模型，随着流量的增大，其扬程下降较快，在大流量工况下，扬程小于该轴流泵模型。通过对比流量-效率曲线可以发现，随着流量偏离设计流量，相较于该轴流泵模型，对旋式轴流泵效率下降较为缓慢，曲线更为平坦，高效区更宽，约为该轴流泵模型2倍，提高了其大流量和小流量时的效率。

图7 对旋式轴流泵与现有轴流泵模型对比Fig.7 Model comparison of counter-rotating axial flow pump and existing axial flow pump

对旋式轴流泵外特性的变化主要由两级叶轮共同决定，但由于前、后叶轮之间的相互影响，其各自的外特性也发生改变，图8给出了不同工况下对旋式轴流泵前、后叶轮的外特性变化规律。由图8可知，设计流量下，后叶轮扬程与预期值接近，且效率较高，说明所设计的后叶轮具有较为优秀的水力性能。前、后叶轮外特性整体变化规律与普通轴流泵相同，随着流量的增大，扬程逐渐降低，由于两级叶轮扬程同时下降，这也造成了对旋式轴流泵扬程下降较快；而效率先升高后降低，前叶轮的流量-效率曲线更加平坦，效率对流量的变化不敏感，在较广的流量空间里保持高效率，这一定程度上解释了对旋式轴流泵高效区较广的原因。同时，不同流量工况下，后叶轮的效率相对较低，这主要由于前叶轮出流的影响，后叶轮的入流条件相对较差。

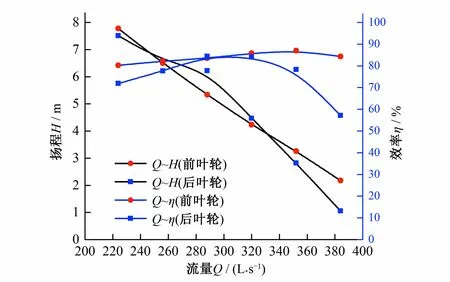
图8 对旋式轴流泵前后叶轮对比Fig.8 Comparison of front and rear impellers of counter-rotating axial flow pump

3.2 空化性能预测与分析

必须空化余量是衡量水泵空化性能的重要指标，用NSPHre表示，利用叶片空化预测模型分析对旋式轴流泵的前、后叶轮的空化性能[13]，该公式为：

(6)

式中：Pin为进口处总压力，此时为101 325 Pa；Pv为叶轮背面靠轮毂侧(叶片展向span=85%处)且距离叶片进口处15%～20%位置的最小压力。运用该公式对南水北调同台试验的多个轴流泵模型进行预测[14]，结果表明该模型能较准确的预测轴流泵的空化性能。

通过公式(6)预测前、后叶轮不同工况下的必须空化余量与上述现有比转速相同轴流泵模型对比如图9所示。由图9可知，小流量工况下，前叶轮的必须空化余量大于该轴流泵模型，随着流量的增大，前叶轮的必须空化余量逐渐减小，而该轴流泵模型先减小后增大，大流量工况下必须空化余量则小于该轴流泵模型，这说明在大流量工况下，相较该轴流泵模型，前叶轮具有更好的空化性能；相同流量下对旋式轴流泵后叶轮的必须空化余量明显小于该轴流泵模型及前叶轮，明显小于前叶轮，说明对旋式轴流泵设计时，应主要考虑前叶轮的空化性能。

图9 对旋式轴流泵与现有轴流泵模型空化性能对比Fig.9 Comparison of cavitation performance of counter-rotating axial flow pump and existing axial flow pump models

3.3 内部流动分析

由前面的分析可知，对旋式轴流泵的外特性已发生较大改变，外特性的改变往往是由内特性引起的，下面结合内流场进一步分析对旋式轴流泵前、后叶轮的相互影响及作用差异。边界涡量动力学(Boundary Vorticity Dynamics，BVD)[15,16]是基于涡动力学研究建立的一套理论，描述通过单位面积内通过单位面积扩散的涡通量的物理量，定义为：

(7)

式中：σ为边界涡量流BVF(Boundary Vorticity Flux)；ω为涡量；v为运动黏性系数；n为流体表面外法线方向的单位矢量。

大量研究表明，边界涡量流对叶片性能有着极大影响，既可以提供升力，又可以产生阻力。对于一般轴流泵，在叶片匀速转动、流体不可压缩、雷诺数较大、壁面无滑移时，BVF主要表现为压力梯度产生的分量σp，即：

(8)

式中：p为任一点的压力值。

由于轴流泵内部水流是沿轴向运动的，故其可简化为σpz的作用，即：

(9)

对于轴流泵叶片，在柱坐标(r，θ，z)，轴向力矩的表示形式为：

(10)

则水流流经叶轮增加的功量G为：

G=ΩMZ

(11)

式中：Ω为转速；M和Mz是作用在叶片表面的力矩；z表示轴向，σpz为轴向压力梯度。

结合式(8)～(10)可知轴流泵叶片的做功能力与压力梯度分布有着较大关系。

图10给出了对旋式轴流泵0.8Q、1.0Q和1.2Q工况下前、后叶轮叶片表面的压力梯度σpz分布情况。由图10(a)可知，在前叶轮压力面的进、出口边和吸力面的进口边均存在着正峰值区，表明这段区域做了负功。随着工况偏移设计工况时，前叶轮叶片压力梯度分布变差，但总体来说分布较为均匀，这说明前叶轮具有优秀的水力性能，也解释了前叶轮在较大流量空间内保持高效率的原因。由图10(b)可知，与前叶轮相比，后叶轮的压力梯度分布相对较差，设计的叶轮与优秀轴流泵模型仍有一定差距。在与前叶轮相同位置出现了正峰值区域，设计流量下，正峰值区域较小，且压力梯度分布较为均匀，但随着流量的偏移设计流量，压力梯度分布恶化严重，这也造成了后叶轮效率下降较快。

图10 对旋式轴流泵轴向压力梯度分布 Fig.10 Axial pressure gradient distribution of counter-rotating axial flow pump

4 结 论

(1)设计流量下，对旋式轴流泵扬程约为8.4 m，效率约为82.3%，与TJ04-ZL-23轴流泵相比，效率有所下降，但扬程提升了约1倍，该对旋式轴流泵具有较为优秀的水力性能。

(2)与现有相同比转速的轴流泵模型相比，小流量工况下，对旋式轴流泵扬程明显大于该轴流泵模型，且对旋式轴流泵高效区明显较宽，约为该轴流泵模型2倍，提高了轴流泵大流量和小流量时的效率。

(3)与前叶轮相比，对旋式轴流泵后叶轮具有更好的空化性能，对旋式轴流泵设计时，应主要考虑前叶轮的空化性能。而前叶轮的效率更高，且在较广的流量空间内保持高效率，这也是对旋式轴流泵高效区更宽的原因。

(4)对旋式轴流泵的前、后叶轮的压力面的进、出口边和吸力面的进口边均存在着正峰值区，但前叶轮压力梯度分布明显优于后叶轮，且随着流量偏移设计流量，后叶轮的压力梯度分布恶化严重，后叶轮的设计与优秀轴流泵模型仍有一定差距。