基于长短时记忆网络(LSTM)的地下水埋深模拟预测——以关中平原为例的实例分析

张朝逢，陈皓锐，岳中奇

(1.陕西省地下水管理监测局，西安 710000；2.中国水利水电科学研究院，北京 100048)

0 引 言

随着国民经济中的高速发展，水资源的开采日益增大，而我国人均水资源占有量仅为世界平均水平的1/4，水资源的缺乏成为限制经济发展的重要因素之一[1, 2]。地下水资源的开发和利用在各行业都占有很大比重[3]。因此，准确预测地下水埋深可为地下水资源的有效管理提供科学依据，对区域水资源合理调度以及可持续利用具有重要意义。

地下水埋深影响因素很多，如地形、气象、土壤、人类活动等，在这些因素的综合影响下，地下水埋深在时间序列上具有很强的随机性和滞后性[4-6]。如何准确预测地下水埋深一直是水利领域研究的热点问题之一。目前针对地下水埋深预测的研究方法有很多，有多元回归分析、灰色关联、人工神经网络模型、基于水量平衡的数值模型，等等[4, 6-11]。近些年，我国信息技术迅速发展，许多学者都试图利用数据驱动的方式来预测地下水水位[4, 12]。

最早的为人工神经网络(Artificial Neural Networks, ANN)，早在20世纪90年代就被应用于地下水水位预测当中[13]。递归神经网络(Recurrent Neural Network, RNN)的出现改善了人工神经网络对时间序列数据的模拟精度，也被广泛应用于地下水水位预测的研究中[14-16]。后来为了解决RNN 在长时间序列学习时出现的梯度消失问题，HOCHREITER和SCHMIDHUBER[17]提出了长短时记忆网络(Long Short-Term Memory, LSTM)。由于LSTM在时间序列模拟中具有明显优势，在医药、金融、社会学等多领域中得到了广泛的应用。近些年，水利领域基于LSTM模型的研究也逐渐在开展。殷兆凯[18]等人基于LSTM模型对锦江流域高安站以上部分降雨径流进行了模拟和预报，并与新安江模型进行了对比，在相同的预见期下，LSTM模型比新安江模型有更好的预报性能。ZHANG[19]等人改进LSTM算法，运用土壤特征、地形、气象数据等模拟了河套地区的地下水水位，发现模拟精度较高。HU[20]等对比了LSTM 与ANN 径流产流方面的预测性能，发现LSTM比ANN模型预报得更为精准。LIANG[21]等运用LSTM 模型分析了多年实测三峡水库蓄水水位、放水量等数据与洞庭湖水位数据，发现2者关系密切。

然而，上述研究主要集中洪水和径流的模拟与预报，LSTM模型在地下水水位的模拟研究相对较少，并且已有针对LSTM 模型的参数设置讨论也还不够深入，没有涉及训练次数对模拟精度的影响。本研究基于区域地下水水位的实测数据，基于LSTM 模型，进行地下水埋深模拟，并且探索模型参数对模拟精度的影响以及分析模型误差来源。

1 材料与方法

1.1 研究区概况

关中平原位于陕西省中部，南接秦岭，北抵北山(梁山、黄龙山、尧山、嵯峨山、五凤山、岐山、千山和关山等)，西起宝鸡，东至潼关，是一个三面环山，东部敞开的新生代断陷盆地。关中是陕西省粮棉油的主要产区，耕地面积145.67 万hm2，农业生产总值 1 700.40 亿元，占陕西省的 60.2%。关中平原是暖温带半湿润季风气候，多年平均降水量为 505～718 mm。2017年关中地区地下水供水总量为24.84 亿m3，占该区域总供水量54.89 亿m3的45.25%，占全省地下水总供水量32.57 亿m3的76.27%。其中浅层地下水供水量为24.45 亿m3，占关中地区地下水总供水量的98.43%。目前关中地区地下水超采严重，关中平原地下水埋深大于40 m的面积占总面积的30%，埋深在20～40 m的面积占21%，埋深在8～20 m和4～8 m的面积占23%和12%，埋深小于4 m的占14%。

本研究采用关中平原33个地下水埋深观测井的逐日地下水水位数据，数据长度为2007-2017年，地下水埋深观测井的分布如图1所示。

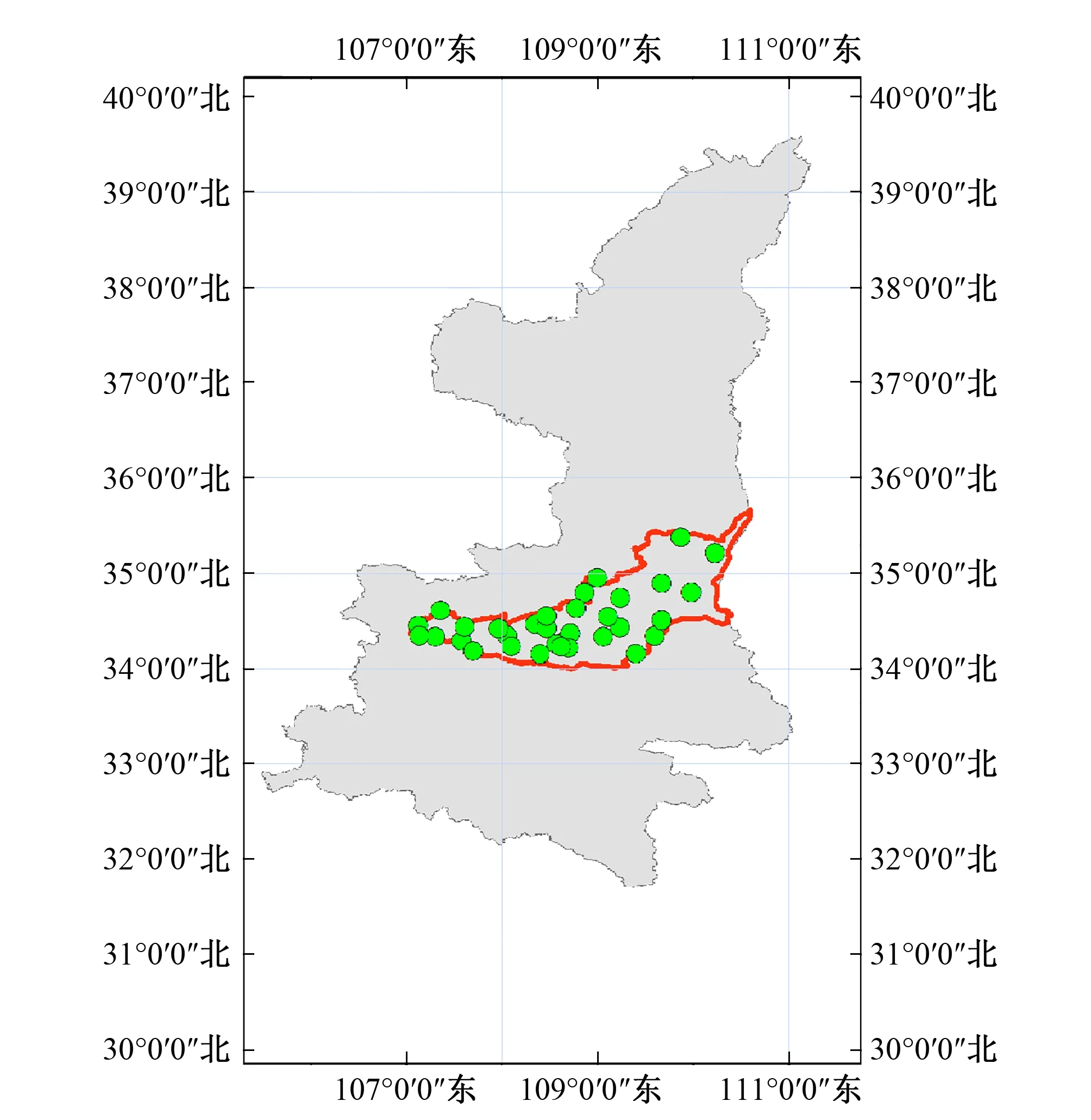
图1 研究区地下水埋深33眼观测井的分布

1.2 长短时记忆网络(LSTM)的构建

长短时记忆网络(LSTM)是一种特殊的时间递归神经网络(RNN)，能有效地避免RNN在长依赖序列模型中出现的梯度弥散问题[17]。LSTM模型包括输入门、遗忘门、输出门和细胞状态等4部分。输入门决定了输入信息向细胞状态传递的多少；遗忘门主要是控制上一时段细胞状态中的信息有多少被遗忘，有多少向当前时刻传递；而输出门则是基于遗忘门和输入门更新的细胞状态，来输出计算结果；细胞状态用来记录当前输入、上一时刻隐藏层状态、上一时刻细胞状态以及门结构中的信息[17, 19]。LSTM 神经网络的整体结构如图2所示。

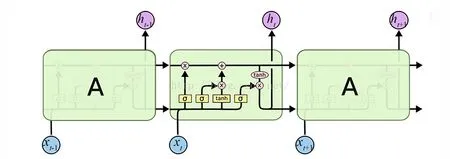
图2 LSTM 神经网络的整体结构

LSTM模型具体计算过程如下。

LSTM在计算过程中，首先计算遗忘门ft。ft控制着从之前的状态中需要去掉信息的多少，其计算公式如下：

ft=σ[Wf(ht-1,xt)+bf]

(1)

式中：Wf和bf为遗忘门的可调参数矩阵或向量，这些参数将会在训练过程被优化；σ为Sigmoid 激活函数。

然后，计算输入门it。it将决定从新获取的信息中选择多少用以更新状态，it的计算公式如下：

it=σ[Wi(ht-1,xt)+bi]

(2)

(3)

式中：Wi、bi、WC和bC都为可调参数矩阵或向量，这些参数将会在训练过程被优化；tanh为双曲正切激活函数。

下一步是将过去与现在的记忆进行合并，计算公式如下：

(4)

接下来计算输出门ot。ot可以决定在t时刻有多少信息生成隐藏层状态变量ht，其计算公式如下：

ot=σ[Wo(ht-1,xt)+bo]

(5)

ht=ottanh (Ct)

(6)

式中：Wo和bo为输出门的可调参数矩阵或向量。

最终，ht传入输出层，再经过计算后得到LSTM在t时刻的最终输出yt:

yt=Wdht+bd

(7)

式中：Wd和bd为输出层的可调参数矩阵或向量，这些参数将会在模型训练过程被优化。

1.3 模型的输入与输出

模型的输入为2007-2017年关中平原33眼地下水埋深观测井的逐月地下水水位观测数据。模型输出为关中平原观测期内对应模拟地下水水位。

1.4 模型的训练与验证

LSTM模型的建立分为训练和验证2个阶段。首先以33眼地下水观测井2007-2017年的逐月观测数据作为一个整体的数据集并随机地将其按照2∶1划分为训练数据集和验证数据集。接着对模型进行训练，在此过程中，分别设置训练次数为10、20、30、40、50、60、70、80、90和100次，分析模型训练和验证阶段的模拟精度，确定最优的训练次数。在模型最优训练次数确定后，利用建立的LSTM模型，分别针对每一眼观测井的数据再进行模拟，评价不同样本容量对模拟精度的影响。

1.5 模型评价指标

为了量化LSTM模型在地下水水位模拟中的精度，本研究采用了3种评价指标，分别为决定系数R2，均方根误差RMSE和相对均方根误差RRMSE。其中R2表示观测值与模拟值的相关性以及模拟值与观测值的吻合度；RMSE则反映模拟值与观测值在数量上的差别，而RRMSE则体现了模拟值与观测值的误差所占观测值的比例。具体的计算公式如下：

(8)

(9)

(1-)

式中：n为总样本数量；Oi为t时刻的观测值；Pi为t时刻的模拟值；Oiave为观测值的平均值。

2 结果与讨论

2.1 长短时记忆方法训练次数的选择

长短时记忆模型的训练次数对模型的预测结果产生很大的影响，因此确定好长短时记忆方法训练次数，是准确预测陕西关中平原地下水埋深的关键。图3给出了10种不同训练次数(10～100次)LSTM模型对关中平原地下水埋深模拟效果评价指标。整体上决定系数R2随着训练次数的增大而逐渐提高，但在训练次数达到40次后决定系数R2变化不大。对于训练阶段，训练次数为60次的R2最高为0.980 43，而在验证阶段，R2在训练次数为40次时最大，为0.981 65。训练阶段和验证阶段均方根误差RMSE和相对均方根误差RRMSE对于训练次数有着相似的结果。均方根误差RMSE在训练次数为40次时最小，而在训练次数为50次和60次时，RMSE相对较大。相对均方根误差RRMSE也有同样的结果。这也说明应用LSTM模型并不是训练次数越多越好，对于特定的样本，如果样本中存在一些带有误差的信息，而训练次数越多，网络精度越高，也意味着记录的错误信息越多，从而导致模拟的精度下降[18]。因此在LSTM模型计算时需要对训练次数与获取的试验数据进行匹配，选择最优的训练次数。在本研究中，选择训练40次作为试验区采用LSTM模型预测地下水埋深的训练次数。

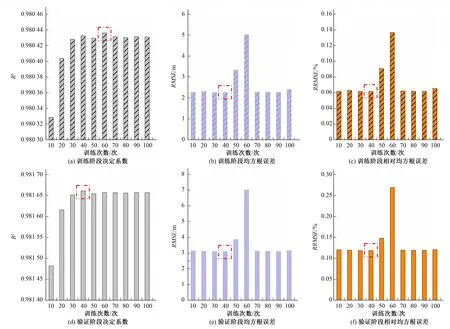
图3 LSTM模型预测评价指标与训练次数的关系注：红色虚线框出的表示该训练次数获得最优模拟精度。

2.2 整体模拟效果

LSTM 模型模拟关中平原地下水水位的整体结果如图4所示。从图4中可以看， LSTM 模型模拟地下水水位的整体效果较好。在训练和验证阶段，决定系数R2均为0.98，这也说明运用LSTM模型可以得到较好的地下水水位模拟结果。然而在验证阶段的均方根误差和相对均方根误差都要大于训练阶段的，表明虽然LSTM模型较好地模拟了关中平原地下水水位的状况，但是模拟精度在验证阶段有所下降。另外，尽管在训练阶段地下水埋深没有大于100 m，但是验证阶段LSTM模型在地下水水位埋深100～120 m区间的模拟精度也很高，这表明LSTM模型通过已有地下水水位数据计算下一时段地下水水位时其模拟范围可以适当的放大。

图4 实测和模拟地下水水位对比

2.3 不同水位观测井的模拟精度差异

图5给出了训练阶段关中平原33眼地下水水位井单独运用LSTM模型进行模拟的3个评价指标值。在训练阶段，R2小于0.23的有2眼井，R2大于0.9的有13眼井。通过分析数据发现，模拟不准的2眼井的地下水水位都有大于5 m的突变点，这也说明LSTM模型在计算时间序列时如果有异常点出现时，会记忆并一直传递下去，从而导致模拟结果失准。对于训练阶段，均方根误差整体来说不大，33眼地下水埋深观测井中只有2眼的均方根误差大于1 m，其余的都小于1 m。相对均方根误差也有相似的结果，33眼地下水埋深观测井中只有2眼的相对均方根误差大于7%。

如图5所示，验证阶段33眼地下水埋深观测井地下水埋深单独模拟的整体效果较好，大多数地下水埋深观测井的R2都在0.6以上，相对均方根误差都小于8%。但是在验证阶段的模拟效果不如训练阶段的。相比训练阶段，在验证阶段R2小于0.23的增加到了4眼，R2大于0.9的只有11眼，并且均方根误差也有所增大，最大的值为20.43 m，大于2.43 m的也有3眼井，最大的相对均方根误差增大到了38%。与将33眼地下水埋深观测井所有观测数据作为一个样本集相比，单独模拟的效果要低于整体的模拟效果，这主要是将33眼井的观测数据单独作为样本集时，样本的数量不够，LSTM模型训练时学习存在偏差，从而导致模拟精度不好。肖晴欣[22]在LSTM预测棉花病虫害的时候也发现类似的问题，整体样本比单一样本的预测精度要好。因此，在以后运用LSTM模型进行地下水水位模拟时应加大样本数量。

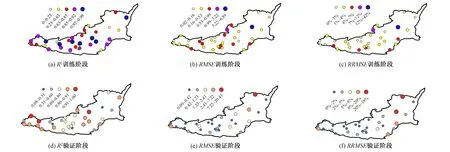
图5 训练阶段和验证阶段33眼观测井单独模拟时各水位井地下水埋深模拟评价指标注：圆圈颜色越深代表其值越大，圆圈直径越大代表其值越大。

2.4 不足与展望

本研究首先通过率定LSTM模型的模型参数(训练次数)，在最优的训练次数下分析了LSTM模型对关中平原整体地下水水位的模拟效果和单独33眼井的地下水水位的模拟效果进行了分析。模型在计算方面也有不足之处，主要表现在如下2方面：在模型算法方面，本研究重点研究训练次数对模拟精度的影响，未考虑网络节点和层数对模拟精度的影响；在模型输入方面，模型主要通过实测的地下水埋深数据来模拟下一时刻的地下水埋深，是通过自相关来预测地下水埋深，未考虑气象条件、人类活动等因素对地下水埋深的影响。因此，今后的研究有必要考虑模型网络结构的影响以及增加其他环境因素作为输入数据，更进一步提高模拟精度。

3 结 论

本文通过长短时记忆网络模型对关中平原地下水水位进行模拟，模型输入为关中平原33眼地下水埋深观测井在2007-2017年的逐月地下水水位观测数据，利用LSTM模型在时间序列上模拟的优势，采用前一时段的地下水埋深观测数据来模拟下一时刻的地下水水位，得到以下研究结论。

(1)LSTM在模拟关中平原地下水埋深时，模型训练次数对模拟精度产生明显影响，模拟精度在训练次数为40次时最佳。

(2)在选择最优训练次数下，LSTM模型可以较好模拟关中平原的地下水埋深变化，R2在训练阶段和验证阶段都能达到0.98，RMSE和RRMSE也较小。

(3)以33眼地下水埋深观测井的观测数据单独作为一个样本集时，LSTM模型的模拟精度比把所有数据当作一个样本集时要差，并且由于样本数据的减少，验证阶段的模拟效果也远不如训练阶段的效果。因此，运用LSTM模型模拟地下水埋深变化是应加大样本数量，以得到更好的模拟效果。