基于内点法的热工数据鲁棒校正方法

熊志强， 朱小良， 任少君， 董鸿霖

(东南大学 能源与环境学院， 南京 210096)

随着我国“节能、减排、降耗”政策的推进，智慧电厂已经成为了今后电厂发展的新趋势[1],提高在线测量的过程数据的可靠性和准确性是推进智慧电厂深入发展的重要保证，由于测量的模糊不确定性，测量数据不可避免带有误差。过程数据的误差分为随机误差和显著性误差两类。随机误差是在测定过程中一系列有关因素形成的具有相互抵偿性的误差，不能被确定和预测。显著性误差是由仪表故障等引起的，与随机误差比较，显著性误差的幅值更大，其存在会严重破坏数据误差的分布特性，具有显著性误差的数据不仅不能正确反映生产过程的真实情况，而且校正数据时会使显著性误差分摊到正常测量数据上，从而使数据校正后的结果恶化。因此，研究者提出了很多针对显著性误差的检测方法，主要包括基于机理模型的方法(如测量检验法[2]、节点检验法[3]和整体检验法[4])和基于数据驱动的方法(如主元分析法[5-6]、偏最小二乘法[7]、神经网络法[8]等)。

在火电机组中，汽轮机是以蒸汽为工质，并将蒸汽的热能转化为机械能的旋转设备，是主要的生产设备之一。据统计，汽轮机故障引起的火电厂停机事故占火电厂全部故障的30%～50%，其中传感器故障又占汽轮机故障的80%以上，针对汽轮机系统的数据校正是当前工作的重点，因此笔者针对汽轮机系统的回热系统的数据校正进行了研究。传统的数据校正算法的前提是假设测量误差服从正态分布，在满足质量平衡和能量平衡的条件下，利用测量数据的冗余性，使得校正值与对应的测量值的偏差的平方和最小[9]；与此同时，数据校正技术可以将一些难以测量或者暂时不能测量的重要变量通过平衡方程进行估计，有利于设备的性能监测。

1 鲁棒数据校正模型

由于鲁棒数据校正不仅对数据的分布特性不敏感，还能最大限度地消除显著性误差的存在对数据校正结果的影响。因此，笔者提出了一种新的鲁棒数据校正算法，并与传统的鲁棒数据校正算法相比较，仿真研究表明该方法能够有效地减小数据中的随机误差，并且最大程度减小显著性误差的影响，使校正值逼近真实值，通过现场的热力试验进一步验证了方法的正确性。

1.1 传统的鲁棒数据校正模型

传统的鲁棒数据校正[10]的过程参数的基本测量模型可以表示为：

xi=x0i+ei+δi

(1)

式中：xi为第i个测点的测量值；x0i为真值；ei为测量误差；δi为显著性误差。

针对该模型，其前提条件是测量值服从正态分布，可得测量值向量x的最大似然函数L(x)为：

x=(x1,x2,x3,…,xm)

(2)

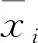
根据最大似然原理，使似然函数最大时的xi是过程变量真值的最大似然估计值，对式(2)进行对数似然估计，则使目标函数γ最小时就使似然函数最大，即

(3)

约束条件由质量守恒和能量守恒定律等组成，过程变量的真实值需要满足这些约束方程，因此数据校正值也应该满足这些约束方程，即数据校正问题转化成了有约束的数学优化问题。

用影响函数fIF(ε)评估鲁棒校正函数的效果，其公式为：

(4)

式中：ρ(ε)为给定的鲁棒校正函数；ε为相对残差。

热力过程数据可能包含显著性误差，所以其误差分布往往是不确定的，如果用经典的数据校正算法得不到太好的校正结果，所以开发了鲁棒校正算法，该算法对大的显著性误差不敏感，并且可以减小显著性误差造成的影响。大多数的鲁棒校正算法都是基于鲁棒校正理论开发的，根据鲁棒校正理论，具有很大相对残差的变量，其权重应该较小。

目前，被广泛使用的鲁棒校正函数有Fair函数、Welsch函数、Cauchy函数、Hampel函数、Correntropy函数等[11]，加权最小二乘(WLS)函数和各鲁棒校正函数的形式如下：

WLS函数为

(5)

Fair函数为

(6)

Welsch函数为

(7)

Cauchy函数为

(8)

Correntropy函数为

(9)

Hampel函数为

(10)

式中：CF、CW、CC、CCo、CP、AH、BH、CH为各函数中可调整的常数，根据不同的研究对象凭经验选取。

1.2 笔者所提出的鲁棒数据校正模型

笔者提出的鲁棒校正函数为：

(11)

式中：CP为可调整的常数，根据研究对象的随机误差幅度进行调整，目的是在不影响正常数据校正结果的前提下尽可能降低显著性误差对数据校正的影响。

图1为各类鲁棒校正函数和影响函数的图像。

由图1可知：WLS函数和Fair函数、Welsch函数、Cauchy函数的鲁棒校正函数是发散的；Correntropy函数、Hampel函数和笔者提出的函数是收敛的，即这几个目标函数在误差变大时，其分量的估计量是有界的。笔者提出的鲁棒校正函数随着相对残差的变大而最终收敛到1，并且其影响函数也先增大后减小，迅速收敛到0。

2 显著性误差的识别

2.1 测量检验法

对热工过程的数据中显著性误差的识别和剔除是有必要的。笔者采用测量检验法[2]对显著性误差进行检测，可以将相对残差的大小作为判断是否存在显著性误差的根据。

对应于各个测点的正态分布检验统计量Zi为：

(12)

式中：ei为e的元素；var(ei)为方差。

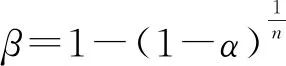
2.2 对鲁棒校正函数的性能评估

笔者采用ηERR和ηEMR对鲁棒校正函数进行性能评估，其中ηERR表示正确识别显著性误差的能力，ηEMR表示误诊率，具体计算公式为：

ηERR=(n1/n2)×100%

(13)

ηEMR=(n3/n4)×100%

(14)

式中：n1为已识别的显著性误差数量；n2为总误差的数量；n3为末识别的显著性误差数量；n4为采样次数。

3 鲁棒数据校正的求解步骤

3.1 内点法

内点法是一种带约束的用来求解线性或非线性的凸优化问题的方法，其基本思想是通过引入惩罚函数将有约束优化问题转为无约束问题，再利用优化迭代过程不断更新惩罚函数，使得算法收敛。

首先构造惩罚函数φ(y,rk)，其一般形式为：

(15)

内点法的流程图见图2。

3.2 基于内点法的鲁棒数据校正的求解步骤

鲁棒数据校正的求解步骤见图3。

4 实例分析

4.1 数值仿真

对一个非线性的仿真模型进行仿真，该系统有6个约束方程，包括5个已测量变量(a1、a2、a3、a4、a5)和3个未测变量(b1、b2、b3)，并且所有的测量变量都是冗余的，未测变量是可观测的，具体模型为：

(16)

该系统各变量的真实值为a=(4.512 4,5.581 9,1.926 0,1.456 0,4.854 0)，b=(11.07,0.614 67,2.050 4)。

化工过程的随机误差一般是真实值的10%左右，与化工过程不同，热工过程的随机误差要比该值小得多，所以在该算例中，测量误差服从正态分布，并取其标准差为0.1，共500组数据，首先不加入显著性误差，然后对原始数据a1添加显著性误差，误差从第101组数据加入，每组加入1个显著性误差，共400组有显著性误差的故障数据，显著性误差从4σ到13σ。

对这些不含显著性误差的原始数据，用各类鲁棒校正函数进行数据校正，将校正后的测量数据及其标准差与真实值及设定的标准差比较。对含有显著性误差的样本，进行数据校正后，再对该鲁棒校正函数的性能评估，其结果见表1和表2。

由表1和表2可以看出：当不含显著性误差时,测量数据的标准差与校正前相比均有一定程度降低，Correntropy函数的性能比较差，耗时也最多，其他4种函数的效果差不多，但是笔者提出的函数耗时最少。

表2 无显著性误差的标准差的校正结果

表1 无显著性误差的测量值和未测值的校正结果

由于篇幅有限，仅列出4个典型的数据校正结果和显著性误差在4σ～13σ的ηERR和ηEMR，具体见图4。

表1(续)

由图4可得：在显著性误差较小时，由于鲁棒校正函数有“抓大放小”的特点，当a1加入的显著性误差为4σ时，与WLS函数相比，还不能明显看出各类鲁棒校正函数的优越性，都存在严重的误差传递现象，其中Welsch函数和Correntropy函数的性能稍差；当a1加入的显著性误差为7σ时，与WLS函数相比，鲁棒校正函数的误差传递程度明显降低，其中笔者提出的函数和Welsch函数相对较好；当a1加入的显著性误差为10σ时，笔者提出的函数的误差传递程度最低，而且a1的数据校正值偏差最小；当a1加入的显著性误差为13σ时，笔者提出的函数几乎不存在误差传递现象，a1的数据校正值与真实值的相对偏差仅为1.55%。比较ηERR和ηEMR可得出：在显著性误差增大时，笔者提出的函数的故障诊断正确率最高，而误诊率最低，在显著性误差达到10σ时，其故障诊断正确率超过了90%，在显著性误差大于或等于13σ时，故障诊断正确率接近100%，证明了笔者提出的函数的优势。

4.2 热工过程的数据校正应用

燃煤电厂中的压力和温度测点通常是按照常规方法来维护和校核的，一般不会含有显著性误差，而流量测点仅在安装前校准一次，并且重要的流量测点大都采用差压式流量计，辅助流量一般采用标准流量孔板测量，如过热、再热减温水流量等。在机组长期运行过程中，由于给水的冲刷和腐蚀，很容易发生精度下降甚至出现故障，使得测量值不准确，会对火电机组的热经济性、机组运行效率和热耗率等厂级指标的计算结果产生影响，进一步影响火电机组的控制，因此流量测点的测量准确性对电厂在线性能监测具有重要意义。

在火电机组回热系统中，为了减少压力损失，主蒸汽管道一般不安装测点，主蒸汽流量一般通过低压加热器(简称低加)进入除氧器水流量或者高压加热器(简称高加)的最终给水流量求得，除氧器入口水的流量可以通过凝结水流量计算得到，给水泵的出口流量通过差压式流量计测量得到，再热减温水和主给水流量又可以通过仪表测出，由电厂能量和质量平衡原理可知，给水泵出口流量、低加进入除氧器水流量和高加的最终给水流量构成了冗余度为2的测量系统。虽然这3个流量冗余度为2，但是由于各自的精度不同、计算方式不同，造成用其中任意1个流量去计算另外2个流量的结果均不相等，均不能满足质量和能量守恒定律。传统的方法一般取高加最终给水流量或者三者求平均值来计算主蒸汽流量，这就造成了冗余信息的浪费，数据校正技术能够通过测量冗余使其在调整度最小的前提下得到最合理的测量数据，同时也可以通过该测量冗余来检测其测点的显著性误差。

图5为国内常见的600 MW亚临界回热式火电机组的给水系统的示意图，其主要设备包括一级、二级、三级高加，给水泵和除氧器。该系统共有24个测点，8个未测参数已说明，其他数据为测量值。

针对该汽轮机的回热系统，首先采取一段稳态的测点数据，系统是否处于稳态通过采用滑动窗口法采样进行判定,判断系统处于稳态的标准参数为汽轮机的功率，是否稳态运行由指标SSD[12]确定：

(17)

式中：N为时间窗内测点的个数；t为时间窗的最后一个测点对应的下标；Ppj为该时间窗内的功率平均值；Ph表示在h采样点的功率(t-N+1≤h≤t)。当SSD<0.015时，可以认为该时间窗内的数据为稳态的。现场测点的测量时间间隔为30 s，时间窗测点数为60，最终采集到200组数据。

由于热工过程测量仪表的随机误差往往是未知的，故要对其随机误差进行估计。显著性误差会破坏数据的分布，热工过程中由于不确定所取的数据中是否包含显著性误差，故不能直接计算这些数据的标准差，而是先假设随机误差遵循零均值的正态分布，剔除离散点，对数据零均值化，然后对这些随机误差取95%置信概率的区间分布[-δI,δI]，根据标准正态分布函数的分布规律，此时的标准差σSD[13]为：

σSD=δI/1.96

(18)

在该回热系统中，系统的约束方程与化工过程的约束方程类似，主要包括质量平衡和能量平衡方程，具体见表3，h(p,t)为在一定的温度t和压力p下的蒸汽或者水的比焓，hsat(p)为在一定的压力p下的饱和蒸汽的比焓。

表3 约束方程

现场数据的测量值及标准差见表4～表6，机组功率平均值为458.43 MW。

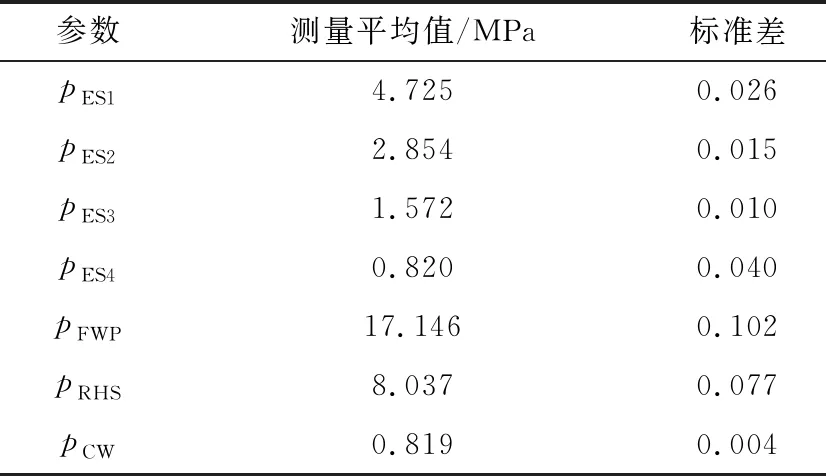
表4 现场压力测量值和标准差

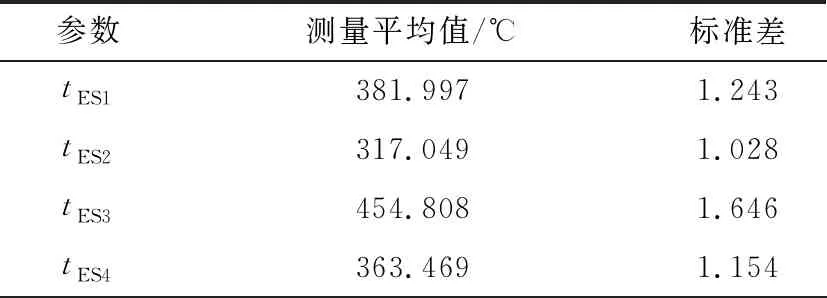
表5 现场温度测量值和标准差

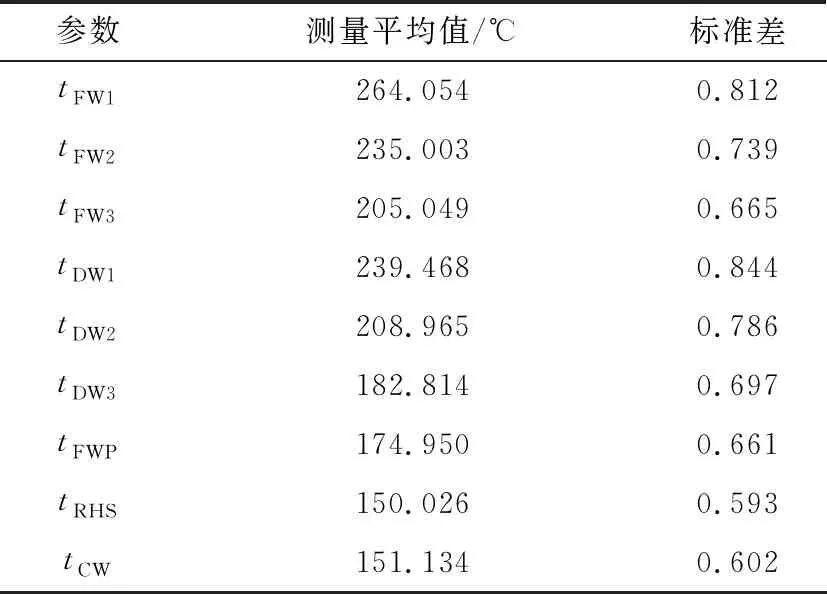
表5(续)

表6 现场质量流量测量值和标准差

由表4～表6可得：温度和压力测量值的标准差很小，与测量值的比值基本在0.4%以内，而3个冗余流量(qm,FFW、qm,FWP、qm,CW)测量值的标准差却相差很大，且随机误差也很大，故引入鲁棒目标函数，对给水泵的出口流量，添加标准差为8σ的显著性误差，验证笔者提出的函数的性能，结合测量检验法对显著性误差进行诊断，鲁棒校正函数为：

p(qm,FFW,qm,FWP,qm,RHS,qm,CW)=

(19)

表7为未测质量流量的估计值，表8为已测质量流量的校正值和标准差。

表7 未测质量流量的估计值

表8 已测质量流量的校正值和校正后的标准差

给水质量流量校正前后对比见图6。由图6可得：测量数据在满足数学模型的前提下，通过测量冗余对各设备出口质量流量进行校正，所得质量流量的标准差均有不同程度的下降，且3个冗余流量的校正值更加符合常理，故障诊断正确率也达到了85%以上，误诊率在10%以下，表明笔者提出的函数可以有效提高测量数据的准确性。

5 结语

笔者基于鲁棒校正原理，提出了一种新的鲁棒校正函数，结合内点法对具有随机误差和可能具有显著性误差的测量值进行数据校正，利用非线性的数值案例与Fair函数、Cauchy函数、Welsch函数、Correntropy函数等进行比较，仿真计算结果表明：显著性误差在4σ～13σ时，该函数的故障传播程度最小，计算速度快，且故障诊断正确率高、故障误诊率最低，具有良好的性能。最后结合现场数据发现其有良好的效果，为电厂的性能监控提供了更为可靠的数据。

由于火电机组的热工过程具有大时滞的特点，并且回热系统还存在相变换热、金属蓄热等扰动，所以在回热系统变工况的过程中，目前还没有准确的动态模型，因而无法用于回热系统动态过程的数据校正，未来的工作要对回热系统的动态过程的机理进行更加完备的分析，得到精确的数学模型，鲁棒数据校正方法才能用于动态的热工过程。