竖向荷载作用下框架厚筏基础的弯矩计算分析

周圣斌

（建研地基基础工程有限责任公司，北京 100013）

0 引言

整体式框架厚筏基础在竖向荷载作用下受到局部弯曲和整体弯曲的影响，其整体工作性能较为复杂［1］。其筏板的弯矩分布规律是设计者所关心的，本文通过数值计算分析对以下问题进行了研究。

1）编制了有限压缩地基上的框架筏板基础有限元计算程序［2］，对筏板基础的弯矩进行计算分析，并与倒梁法进行对比分析，说明倒梁法的适用范围及误差；

2）计算研究了大底盘框架厚筏基础弯矩分布规律，说明了整体弯矩对筏板内力设计的影响，并给出了由于差异沉降对筏板配筋的影响。

1 单独主楼荷载作用下的筏板弯矩

以下为框架厚筏基础的数值计算分析，在计算模型中，构件尺寸采用实际工程常用的尺寸，筏板厚度为 2 000 mm，混凝土强度等级为 C30，筏板边端外挑 1 600 mm。框架柱距为 8 000 mm×8 000 mm，框架梁尺寸为 5 0 0 m m×75 0 m m，框架柱尺寸为 1 200 mm×1 200 mm。带有两层地下室，地下 1 层楼板厚度为 200 mm，顶板厚度为 400 mm，层高取 3.6 m。地面以上 20 层主楼，每层荷载标准值按 15 kN/m2。地基土压缩模量取 15 MPa，回弹再压缩模量取 45 MPa。计算模型的剖面图如图 1 所示，图中阴影部分为主楼投影部分。计算筏板弯矩时采用荷载基本组合，图 2 为单独主楼计算模型平面示意图。

图1 计算模型剖面示意图

图2 单独主楼计算模型（test0）

图3 均匀柱荷载下时筏板弯矩

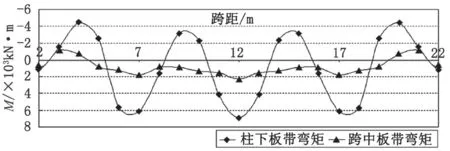
图4 不均匀柱荷载下时筏板弯矩（边柱与中柱荷载比为0.8）

图5 不均匀柱荷载下时筏板弯矩（边柱与中柱荷载比为0.5）

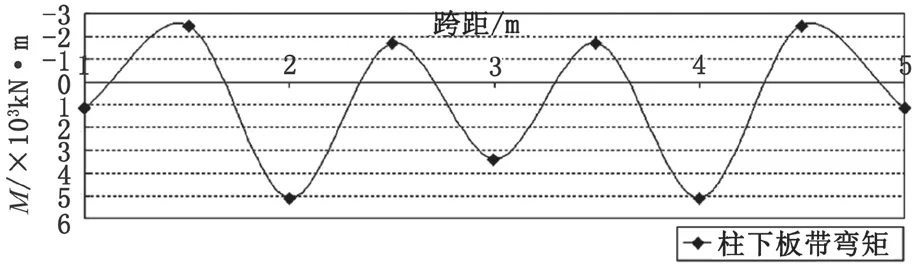
图6 倒梁楼盖法计算筏弯矩

图 3～图 5 为不同荷载情况下筏板弯矩整体分析法计算值；图 6 为倒梁法计算弯矩值。（上述弯矩图为 2 m宽板带的弯矩图，弯矩均为沿筏板纵向轴线分布的弯矩）。计算结果表明，当柱荷载差异较大时采用倒梁法计算弯矩误差较大。

表 1～表 4 为有限元整体分析法和倒梁法筏板弯矩计算值。

计算结果显示柱下板带弯矩大于跨中板带的弯矩，筏板最大弯矩发生在支座处，支座外 1/4 柱跨外弯矩减少明显。跨中板带受到整体弯矩的影响，配筋率约为 0.10 %～0.19 %。

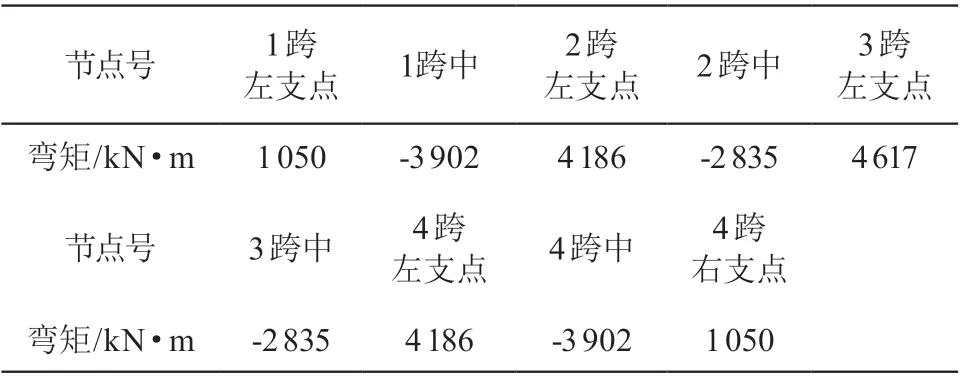
表1 均匀柱荷载下时筏板弯矩（有限元计算结果）

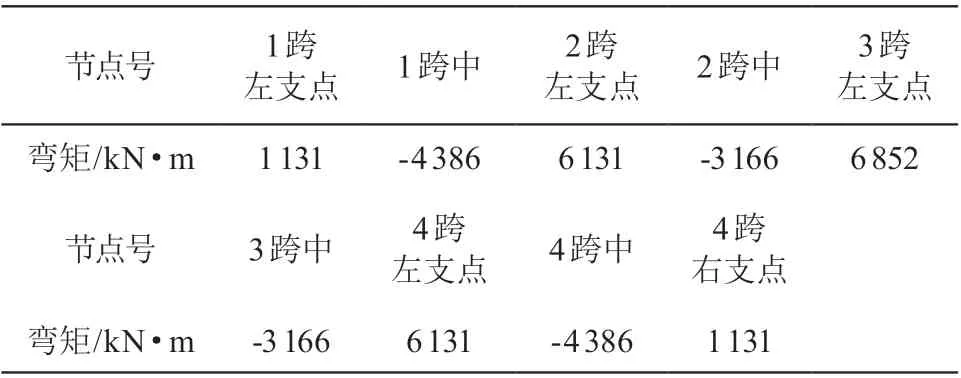
表2 边柱中柱荷载比为 0.8 时筏板弯矩（有限元计算结果）

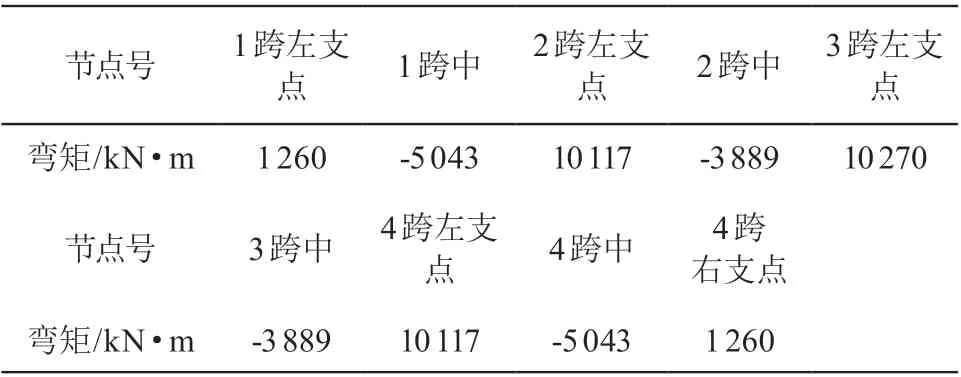
表3 边柱中柱荷载比为 0.5 时筏板弯矩（有限元计算结果）

表4 倒梁法计算筏板弯矩

倒梁法计算结果显示底部最大受拉钢筋配筋率为 0.22 %，跨中最大上部配筋率为 0.10 %。

整体分析法（有限元协同计算分析）计算结果显示：边柱中柱荷载比为 0.5 时筏板底部最大受拉钢筋配筋率为 0.44 %，跨中最大上部配筋率为 0.22 %（整体挠曲为 0.31 %）；边柱中柱荷载比为 0.8 时筏板底部最大受拉配筋率为 0.30 %，跨中最大上部配筋率为 0.19 %（整体挠曲为 0.2 %）；均匀柱荷载下时筏板底部最大受拉钢筋配筋率为 0.20 %，跨中最大上部配筋率为 0.16 %（整体挠曲为 0.1 %）。

倒梁楼盖法假定支座处没有差异沉降，其计算弯矩为局部弯矩。从以上计算结果可以看出当荷载较为均匀时，倒梁法计算结果和有限元计算较为接近，当柱荷载差异超过 20 % 时，计算结果差异较大，筏板弯矩计算需考虑整体弯矩的影响。

2 大底盘框架筏板弯矩的计算分析

以下模型计算反映裙房和主楼基础整体连接时筏板的变形、反力和弯矩分布规律，图 7 为计算模型平面图。图 8 为计算模型中轴线的筏板弯矩图。

图7 四种计算模型平面示意图

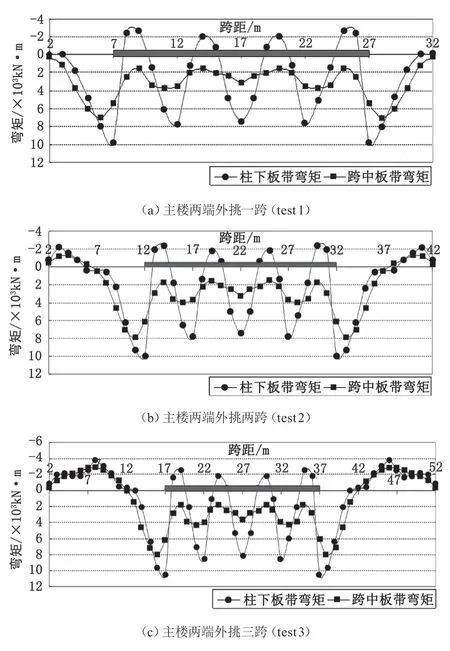
图8 计算模型中轴线的筏板弯矩图

图9 筏板弯矩简化计算图

由图 8 中主裙楼整体连接情况筏板弯矩计算图可见，随着主楼外挑跨数的增加，主楼下弯矩变化不大，弯矩最大发生在主裙楼整体连接处，该处弯矩在 1/4 柱跨外显著衰减，筏板外第 2 跨附近出现反弯现象。计算结果显示：在 20 层主楼荷载作用下主楼下底部受拉钢筋配筋约为 0.35 %；主裙楼交接处底部受拉钢筋配筋率约为 0.45 %；筏板上部受拉钢筋约为 0.1 %。双塔楼计算模型显示，主楼间筏板差异沉降较小，该处筏板受力主要受到局部弯矩的影响。

以上计算结果显示：柱下板带弯矩最大，跨中板带弯矩最小；筏板弯矩至主楼外逐步衰减，到主楼外第 2 跨筏板弯矩已经很小了，构造配筋即可满足抗弯承载力要求；当两主楼荷载相同时，该区域筏板弯矩较小；主裙楼整体连接处筏板配筋应考虑差异沉降引起的附加弯矩。

3 简化分析

竖向荷载作用下筏板弯矩为基底反力所产生的局部弯矩和筏板沉降引起的整体弯矩。一个板带的筏板弯矩的简化计算模型为多跨连续梁。计算简图如图 9 所示。

1）两端固定梁转角位移方程：

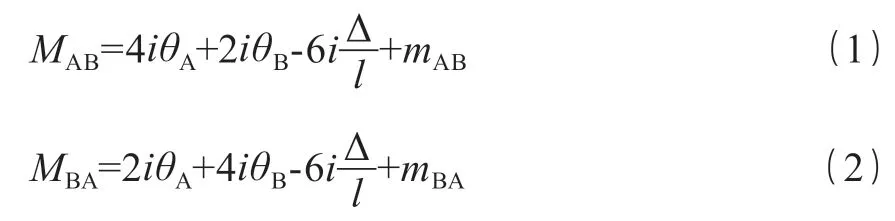
2）端固定一端铰支梁转角位移方程：

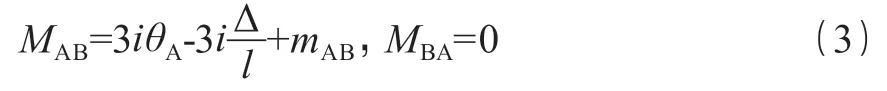
式中：MAB为 A 支座到 B 端的弯矩，kN·m；θA为 A 点转角，°；mAB为 B 端处的固端弯矩，kN·m；MBA为 B 支座到 A 端的弯矩，k N·m；θB为 B 点转角，°；mBA为 A 端处的固端弯矩，kN·m；Δ 为位移量，m；l 为梁的长度，m；i 为线抗弯刚度。

在由结点角位移处，建立结点的力矩平衡方程，解方程，将已知的结点位移代入各杆端力表达式，即可以做出弯矩图。

以下以两端外挑三跨模型（test 3）计算不同荷载等级下整体式筏板的变形和反力，进而简化计算筏板弯矩，目的是探讨不同变形和基底反力情况下的整体式筏板在竖向荷载作用下整体弯矩和局部弯矩，如图 10 所示。

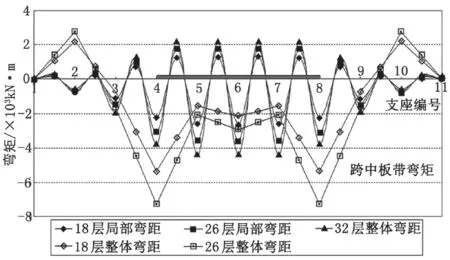
图10 筏板跨中弯矩图

在 18 层楼面荷载作用下：主楼相对挠曲为 0.021 %，主楼下基底反力约为 210 kPa。主楼下由整体弯曲引起的最大配筋率约为 0.1 %（筏板底部钢筋）；反力产生的局部弯曲配筋率约为 0.12 %（筏板底部钢筋）、0.06 %（筏板上部钢筋）。

在 26 层楼面荷载作用下：主楼相对挠曲为0.029 %， 主楼下基底反力约为 340 kPa。主楼下由整体弯曲引起的最大配筋率约为 0.13 %（筏板底部钢筋）；反力产生的局部弯曲配筋率约为 0.16 %（筏板底部钢筋）、0.08 %（筏板上部钢筋）。

在 32 层楼面荷载作用下：主楼相对挠曲为 0.044 %，主楼下基底反力约为 410 kPa。主楼下由整体弯曲引起的配筋率约为 0.2 %（筏板底部钢筋）；反力产生的局部弯曲配筋率约为 0.2 %（筏板底部钢筋）、0.1 %（筏板上部钢筋）。

为探讨差异沉降引起的附加弯矩，取不同差异沉降计算其相应的整体弯矩及筏板配筋率，计算结果如表 5 所示。

主楼相对挠曲为 0.02 %～0.05 % 时，主楼下整体弯矩产生的配筋率约为 0.1 %～0.23 %。主楼下基底反力在 210～410 kPa 时，筏板底部局部弯矩产生的配筋率约为 0.12 %～0.2 %，筏板上部配筋率约为 0.06 %～0.1 %。

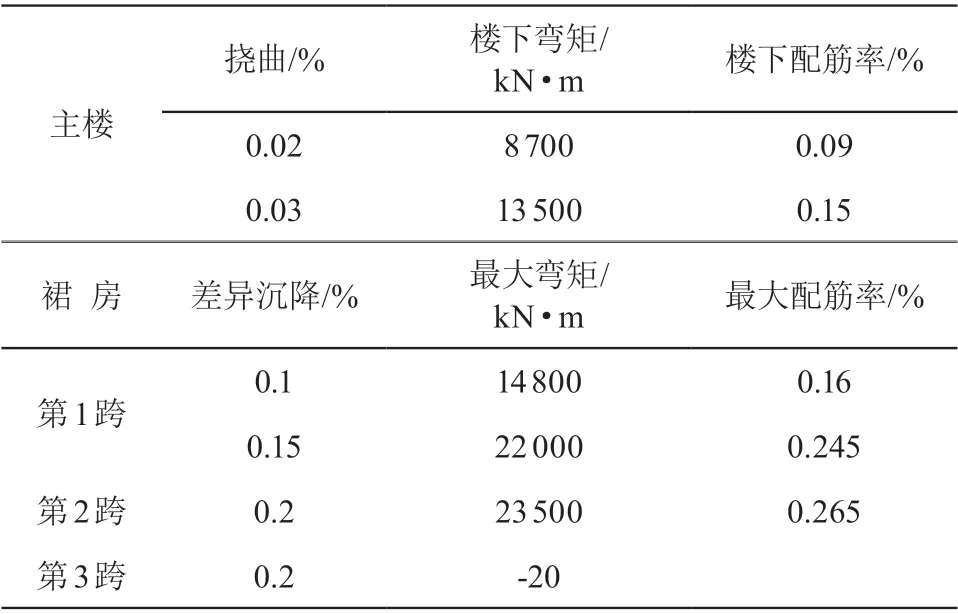
表5 整体弯矩及相应的配筋率

主裙楼整体连接时，筏板局部弯矩从主楼至外逐步衰减，最大的整体弯矩发生在主楼外第 1 跨。第 1 跨差异沉降为 0.1 %～0.15 % 时，最大配筋率为约为 0.16 %～0.25 %；第 2 跨差异沉降为 0.2 % 时，最大配筋率为约为 0.26 %，发生在第 1、2 跨交界处。

4 结论

1）当荷载较为均匀时，筏板弯矩的倒梁法计算结果和整体分析方法较为接近，当柱荷载差异超过 20 % 时，计算结果差异较大，筏板弯矩计算需考虑整体弯矩的影响。该结论与 GB 5007－2002《建筑地基基础设计规范》［3］中所规定的筏板弯矩计算原则相同。

2）主楼下筏板弯矩在柱下板带最大，跨中板带最小，支座弯矩在柱外 1/4 柱跨衰减明显，支座处附加钢筋宜向外延伸 1/4 柱跨；主裙楼整体连接时，筏板局部弯矩从主楼至外逐步衰减，最大的整体弯矩发生在主楼外第 1 跨，该处筏板配筋应考虑整体弯矩的影响。一般情况下差异沉降为 0.1 %～0.15 % 所引起的钢筋配筋率增加约为 0.16 %～0.25 %。