一种新的检测技术——剪切拉拔综合法

朱跃武

（中国建筑科学研究院有限公司深圳分公司，广东 深圳 518057）

0 引言

剪切拉拔综合法是将拉脱强度和原位单剪强度通过前期处理，如：相加求代数和，作为综合法数据的自变量代入一元幂函数曲线，换算混凝土抗压强度值，或将“拉脱强度”和“原位单剪强度”作为自变量带入二元幂函数方程换算混凝土抗压强度。为了提高曲线精度，在已有技术的基础上，对剪拉综合数据中的异常值进行剔除，最终形成拉剪综合曲线，本文将对剪切拉拔综合法进行系统的分析和工程验证。

1 微破损技术的形成基础

混凝土作为量大面广的建筑材料，在我国工业与民用建筑中应用非常广泛，为了确保工程的安全质量，国家相关规范规定了混凝土的验收标准，比如采用与浇筑混凝土同条件标准立方体试件，在标准养护条件下，用28 d 龄期的混凝土抗压强度作验收值。

为了研究可溯源的混凝土强度检测技术，论文先研究立方体试件抗压试验的破坏机理。试件靠近垫板附近因约束的作用，中间部分混凝土纵向受压横向扩张，使外围混凝土受拉，破坏是由外围混凝土纵向劈裂，垫板附近混凝土承受剪切力形成角锥型破坏面，从试件的破坏形态看，主要由中间的多个劈裂柱体和两端的剪切椎体组成，立方体试件的极限抗压力取决于试块形成多个独立受拉劈裂抗拉柱体时的抗拉强度和形成两端椎体的剪切强度。微破损检测技术均是基于压、拉、剪不同参数建立与立方体试件抗压强度的拟合关系后再换算混凝土抗压强度，立方体试件受压破坏与相关的检查方法如图 1 所示。

图1 立方体试件受压破坏与相关的检查方法（单位：mm）

传统的钻芯法检测混凝土强度，是从宏观到微观，即在试件抗压过程中，通过试件受压后发生的剪切、劈裂抗拉使试件被分成无数个独立单元，汇集这些剪切和抗拉强度值最终溯源混凝土的抗压强度，如式（1）所示。

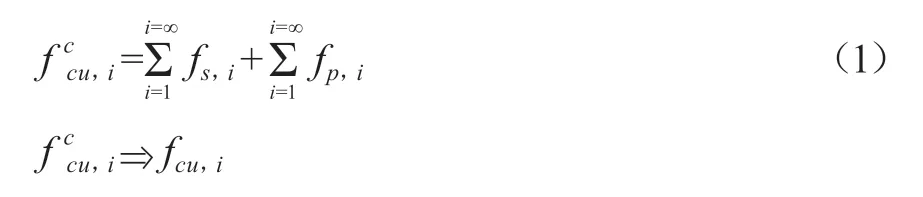
钻芯法具有较好的直观性，其抗压强度相当于同条件、同龄期立方体试件强度。但它也有不足，对结构损伤大，容易损伤构件内的钢筋，试件需要加工打磨和抗压，过程造成能源消耗和垃圾增多。

通过不同方法采集这些自身力学参数，可以得到较高的相关性拟合曲线，由于检测时会对混凝土结构产生微小破损，对此简称微破损法或称直接法。我国早期常用的主要检测方法包括：钻芯法、后装拔出法、后锚固法、剪压法等微破损检测技术，这些方法具有较高的相关性高，误差相比无损检测低的特点，但也存在工艺复杂，因加工试件引入一些数据间的离散情况，还存在对结构损伤较大等不足。随着社会和经济的发展，人们逐渐提高了安全标准，目前建筑物的抗震设防烈度普遍提高，结构的含钢量增大，导致钢筋间距变密，已有的钻芯法会因为直径较大而损伤钢筋而遭受用户质疑，为使微破损检测减少对结构的损伤，不损坏钢筋，其他几种微破损检测方法也因在面对高强混凝土检测，出现数据离差变大的情况发生。

为了解决遇到的问题，人们先后推出旨在解决钢筋密集构件检测的新技术，考虑到泵送混凝土工艺的推广，骨料粒径已受到严格的控制，我们先后研发了《拉脱法》和《原位单剪法》等检测技术，两种检测技术都是在原位对直径Ф44 mm，深度 44 mm 的芯样试件进行拉脱或剪切，拉脱法主要检测胶凝材料的强度，剪切法主要是检测混凝土中粗细骨料的强度，两者侧重不同的材质特性，但这些方法在不同的强度区存在不同的问题，最大的问题就是，测试结果的标准差因芯样直径较小，变得较大，直接影响测试精度［1-7］。

2 剪切拉拔综合法

如何改善微破损检测技术的问题，简化检测方法，减少对结构的损伤，提高检测精度，降低标准差，充分发掘形成混凝土强度的各种因素，可以采用剪切拉拔综合法检测混凝土强度技术，利用混凝土拉应力和剪切应力综合换算混凝土抗压强度，该方法像无损检测技术超声回弹综合法一样该法属于一种“微破损综合法”检测技术［8-9］。

2.1 数据拟合分析

根据前面介绍的立方体试件受压破坏的机理，抗压强度实际是由若干个被劈裂的柱体和受压板约束的剪切椎体强度组成的，如果我们在一个试件上同时采集混凝土拉应力和剪应力综合推算混凝土强度，模拟立方体试件压坏过程，一定会达到理想的强度换算结果。

“剪切拉拔综合法”是在实体结构混凝土上钻制直径 Ф44 mm，深度 65 mm 的芯样试件，在原位将试件剪断与拔出，采集剪切强度和抗拉强度，如式（2）所示。

如图 2 所示，通过获取拉脱强度和剪切强度，利用拟合曲线转换为混凝土抗压强度，由于是直接获得混凝土抗拉强度和抗剪强度，属于一种直接法。

为了解剪切拉拔综合法能否综合反映混凝土自身剪切和拉拔参数与混凝土抗压强度的拟合性能，有效提高精度，首先根据全国多家检测、科研、学校、施工和生产混凝土单位采用两种检测方法获得的原始数据，即拉脱值和原位单剪值及对应的立方体试件强度，以立方体试件抗压强度进行比对，将试件强度不超过 15 % 的试件强度进行分组并平均，最终获得拉脱与原位单剪共计 621 组原始数据，并将对应的拉脱与剪切原始数据进行求和，通过第一次拟合，剔除相对误差大于 34 %，共计 30 组异常值，剩余 591 组数据，由于篇幅有限，本文仅列出部分数据，剪切拉拔与归一后的强度数据如表 1 所示。

图2 剪切与拉脱操作

对表 2 的数据采用spass软件进行拟合分析，分析结果如下。

通过比对曲线参数，发现幂函数曲线相关系数 r 最大，显著性水平 F 比最显著，为此选择幂函数作为拉剪综合法测强曲线。曲线散点图（见图 3）一元幂函数曲线见式（3）：

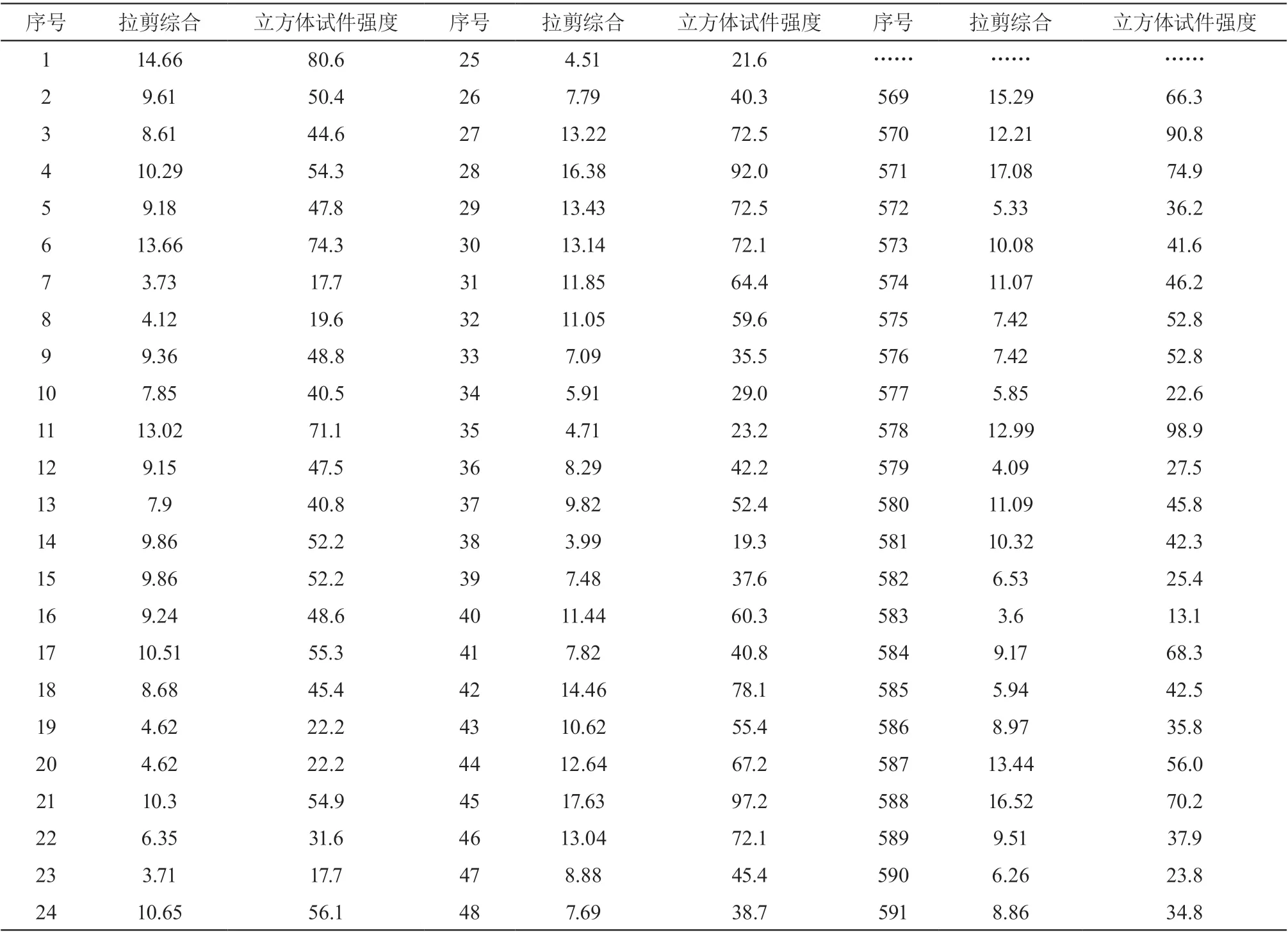
表1 剪切拉拔与归一后的强度数据 MPa

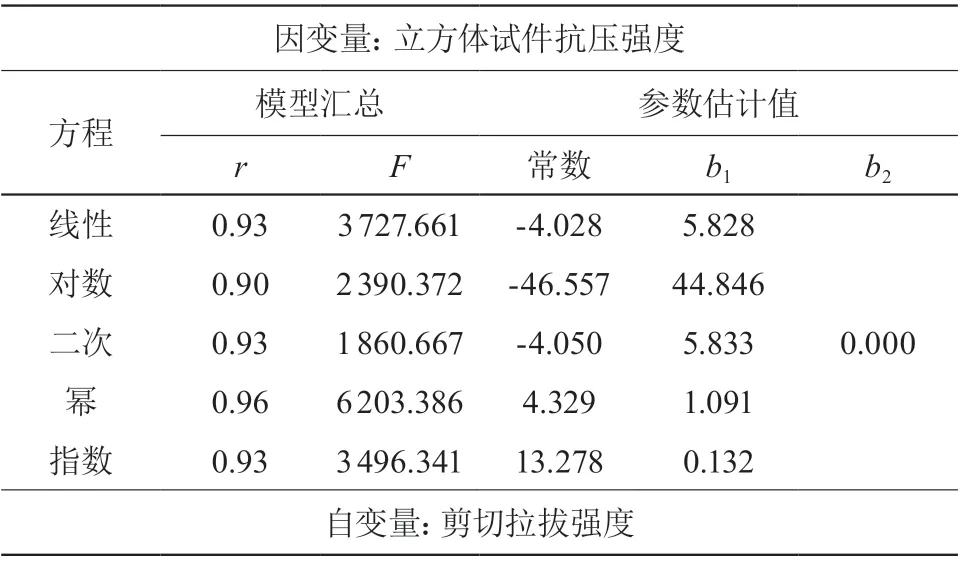
表2 模型汇总和参数估计值

采用剪切拉拔强度作为变量换算出混凝土抗压强度，相关系数 r=0.96，显著性水平 F比=6 203.386，求出其平均相对误差为：б=12 %；平均标准差 S=14 %。可见精度已经达到专用曲线的水平。

同样采用二元幂函数方程对原位单剪强度与拉脱强度和立方体试件抗压强度进行拟合分析，分析结果表明，曲线的相关系数为 r=0.96，平均相对误差为 б=10 %；平均标准差 S=12 %，精度超过一元幂函数曲线，两条曲线平均相对误差和平均标准差都达到专用曲线的水平，二元幂函数曲线方程如式（4）所示。

式中：fs，i为原位单剪强度，MPa；fp，i为拉脱强度，MPa。

2.2 低强区混凝土验证

为了验证该曲线是否满足工程检测的要求，即在同一条件下，其标准差应接近同条件立方体试件强度的标准差，或者小于等于同条件钻芯法的标准差，带着这个问题，我们预制两面试验墙体，尺寸为长 2 m，高度 1.5 m，厚度 0.3 m，一面墙体混凝土设计强度等级为 C35，另一面为 C60，每面墙体预留同条件标准立方体试件 10 组，并分别在墙体上钻取各 10 个直径Ф100 mm 和Ф75 mm 混凝土芯样。并按照剪切拉拔法的技术要求进行原位试验，C35 墙体立方体试件、钻芯和剪切拔出法验证结果如表 3 所示。

表3 C35 墙体立方体试件、钻芯和剪切拔出法验证结果 MPa

对 4 组数据结果采用直方图进行分析，并求出每组数据的平均值和标准差，C35 墙体检测结果的直方图分析如图 4 所示。

通过表 3 和图 4 对 C35 混凝土墙体的试验结果进行分析，采用一元幂函数和二元幂函数曲线计算的强度平均值为立方体试件强度的 83 % 和 81 %，标准差分别为 S=3.494 MPa 和 S=3.431 MPa，其中二元幂函数计算结果的标准差与立方体试件的 S=3.353 MPa 基本相等，并全部小于钻芯法的标准差。

2.3 高强区混凝土验证

同样我们对 C60 墙体也进行相关试验验证，C60 墙体立方体试件、钻芯和剪切拔出法验证结果如表 4 所示。

C60 混凝土属于高强混凝土，由于强度高，钻芯时间长，钻头磨损大，不同直径对强度的影响不同，直径越小，影响越大，同时将试验结果绘制直方图如图 5 所示，求出每组数据的平均值和标准差（S）。

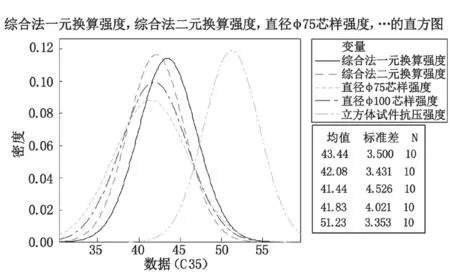
图4 C35 墙体检测结果直方图分析（单位：MPa）

图5 C60 墙体检测结果直方图分析（单位：MPa）

通过表 4 和图 5 对 C60 混凝土墙体的试验结果进行分析，采用一元幂函数和二元幂函数曲线计算的强度平均值为立方体试件强度的 96 % 和 90 %，标准差分别为 S=5.432 MPa 和 S=5.278 MPa，其中二元幂函数计算结果的标准差与立方体试件的 S=4.777 MPa 相差 0.501 MPa，和低强区结果一样全部小于钻芯法的标准差。

为什么在高强区出现拉剪综合法的标准差大于同条件立方体试件，分析其原因，联系钻芯法强度标准差的取值情况，可能是在高强混凝土上钻芯时，因混凝土强度高，钻头磨损快，钻芯时间长，对试件外形会产生一定影响，导致试件产生变形，直接导致拉脱强度偏低，但原位单剪主要剪切混凝土中粗细骨料的强度，因此影响相对要小些，两项因子叠加导致标准差偏大，但均小于钻芯试件抗压强度标准差。

3 结论

1）通过粗差处理后的两体拟合曲线，一元幂函数和二元幂函数的曲线相关系数为 r=0.96。一元幂函数曲线的平均相对误差为：б=12 %；平均标准差：S=14 %。二元幂函数曲线的平均相对误差为：б=10 %；平均标准差：S=12 %，优于一元幂函数曲线，两条曲线均达到专用曲线的水准，由于曲线的计算基础仅来源于 591 组数据样本，作为全国曲线还应增加样本量。

2）在强度低强区，采用一元幂函数和二元幂函数曲线计算的强度平均值为立方体试件强度的 83 % 和81%，标准差分别为 S=3.494 MPa 和 S=3.431 MPa，其中二元幂函数计算结果的标准差与立方体试件的 S=3.353 MPa 基本相等，两条曲线计算结果的标准差全部小于钻芯法的标准差。

3）在强度高强区，采用一元幂函数和二元幂函数曲线计算的强度平均值为立方体试件强度的 96 % 和 90 %，标准差分别为S=5.432 M Pa和 S=5.278 MPa，其中二元幂函数计算结果的标准差与立方体试件标准差 S=4.777 MPa 相差 0.501 MPa，和低强区结果一样全部小于钻芯法的标准差。

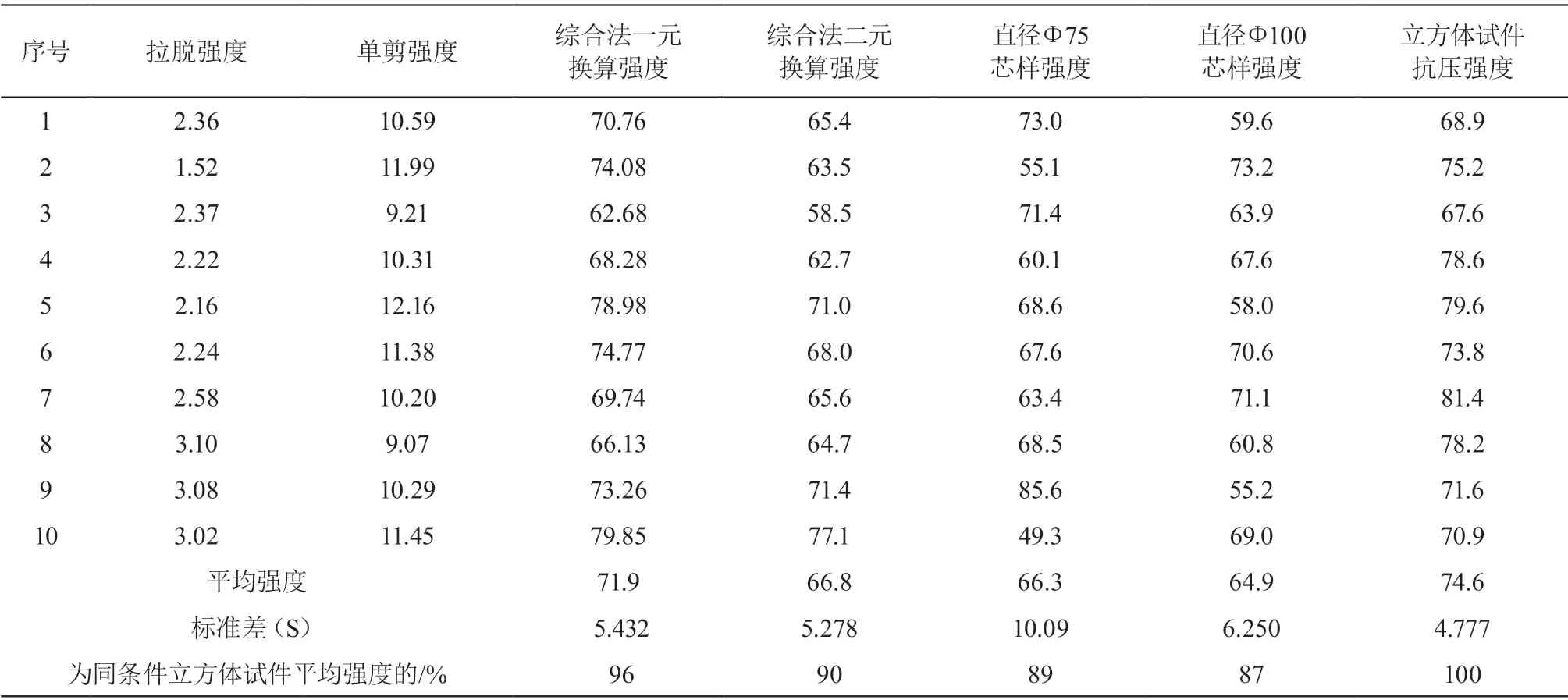
表4 C60 墙体立方体试件、钻芯和剪切拔出法验证结果 MPa

4）无论是在低强区还是在高强区，无论是采用一元幂函数曲线还是二元幂函数曲线，剪切拉拔综合法的强度平均值大于钻芯法强度平均值。

5）剪切拉拔综合法充分利用混凝土内在性能特点，采用微创的剪切和拉拔手段，用钻芯法（直径Ф100 mm）7 % 的混凝土体积创伤，换取比钻芯法更高或相同的检测精度，这对减少结构损伤、节能减排、减少实验室投资、减少废弃物、减轻劳动强度具有重大经济和社会意义。

6）剪切拉拔综合法的研究，开创了检测技术的新思路，该技术具有对结构损伤小，快捷，操作工艺简单的特点，适用于钢筋密集的构件检测。由于可以将试件取出试验，也适合圆形或不规则表面的构件以及混凝土表面遭受冻害或火烧的混凝土强度检测。拉剪综合法除适用与建筑结构混凝土强度检测外，也适用铁路、公路、桥梁和港口码头混凝土工程、装配式混凝土工程的检测。