基于有限元法的轻量化支架力学分析

□ 施云高 □ 杨 爽 □ 陈 红 □ 高思煜

1.常州先进制造技术研究所 江苏常州 213164 2.中国科学院合肥物质科学研究院先进制造技术研究所 江苏常州 213164

1 分析背景

支架是航天载荷的关键支撑部件,要求具有高的支撑强度和低的质量负载。航天载荷的发射方式一般通过运载火箭从地面发射场垂直发射,受火箭运载能力的限制,要求航天载荷在满足任务要求的前提下减轻自身质量[1]。航天器每减轻1 kg质量,将节约发射成本1万～2万美元,具有非常可观的经济效益[2]。可见,需要对航天载荷中的支架进行轻量化设计,并对结构强度进行分析。

2 分析目标

笔者针对航天载荷中的后支架,采用减重的方式进行轻量化设计。基于有限元法[3-5]对轻量化支架在加速度、正弦振动、随机振动、冲击等不同力学工况下的结构应力进行仿真分析,以核验轻量化后支架的结构强度是否满足要求。

3 轻量化支架

针对航天载荷中的后支架,采用开孔减重的方法进行轻量化设计。开孔后支架质量减轻了37.1%,如图1所示。

▲图1 轻量化支架

4 有限元建模

4.1 几何模型处理

为方便划分网格,提高计算效率,笔者将航天载荷系统中除前、后支架和平台外的所有结构体等效为一质点。质点的质量、质心、惯性主力矩与所等效结构的相应参数一致,质点通过远程连接的方式与航天载荷前、后支架的安装面连接。忽略模型中的螺纹孔、圆角、倒角等微小结构。平台与外界柜体通过螺栓紧固连接,将螺栓紧固区域简化为同等接触面积的方形区域。

简化处理后的几何模型如图2所示。

▲图2 简化处理后几何模型

4.2 网格划分

各部件之间采用ANSYS Workbench软件中的Bonded接触单元进行连接,采用Tet10四面体网格和Hex20六面体网格进行网格划分。模型中共有410 214个单元、743 318个节点,网格质量评价指标纵横比最大值为88.642。网格划分后有限元模型如图3所示。

▲图3 网格划分后有限元模型

4.3 力学条件

4.3.1 加速度

加速度条件见表1。模型中各约束点施加固定约束,同时施加X、Y和Z三个方向的加速度。

表1 加速度条件

4.3.2 正弦振动

正弦振动条件见表2。正弦振动激励施加在模型中的固定约束位置处,加载的方向包括X、Y和Z三个方向。

表2 正弦振动条件

笔者将位移激励转换为加速度激励进行分析,令正弦振动的位移y为:

y=Lsin(2πft+φ)

(1)

对位移二阶求导,得到加速度y″为:

y″=-(2πf)2Lsin(2πft+φ)

=-(2πf)2y

(2)

式中:f为频率;t为时间;φ为相位;L为位移幅值。

根据式(2)可计算出4～10 Hz范围内不同频率下的加速度幅值。

正弦振动的激励曲线如图4所示。

▲图4 正弦振动激励曲线

4.3.3 随机振动

随机振动条件见表3。随机振动激励施加在模型中的固定约束位置处,加载的方向包括X、Y和Z三个方向。

表3 随机振动条件

表3中1 dB/oct的计算式为:

(3)

式中:W0为参考功率谱密度;W为相对于W0时的计算功率谱密度;f0为参考频率。

根据式(3)可以计算出10～50 Hz和300～2 000 Hz范围内不同频率下的功率谱密度。随机振动的激励曲线如图5所示。

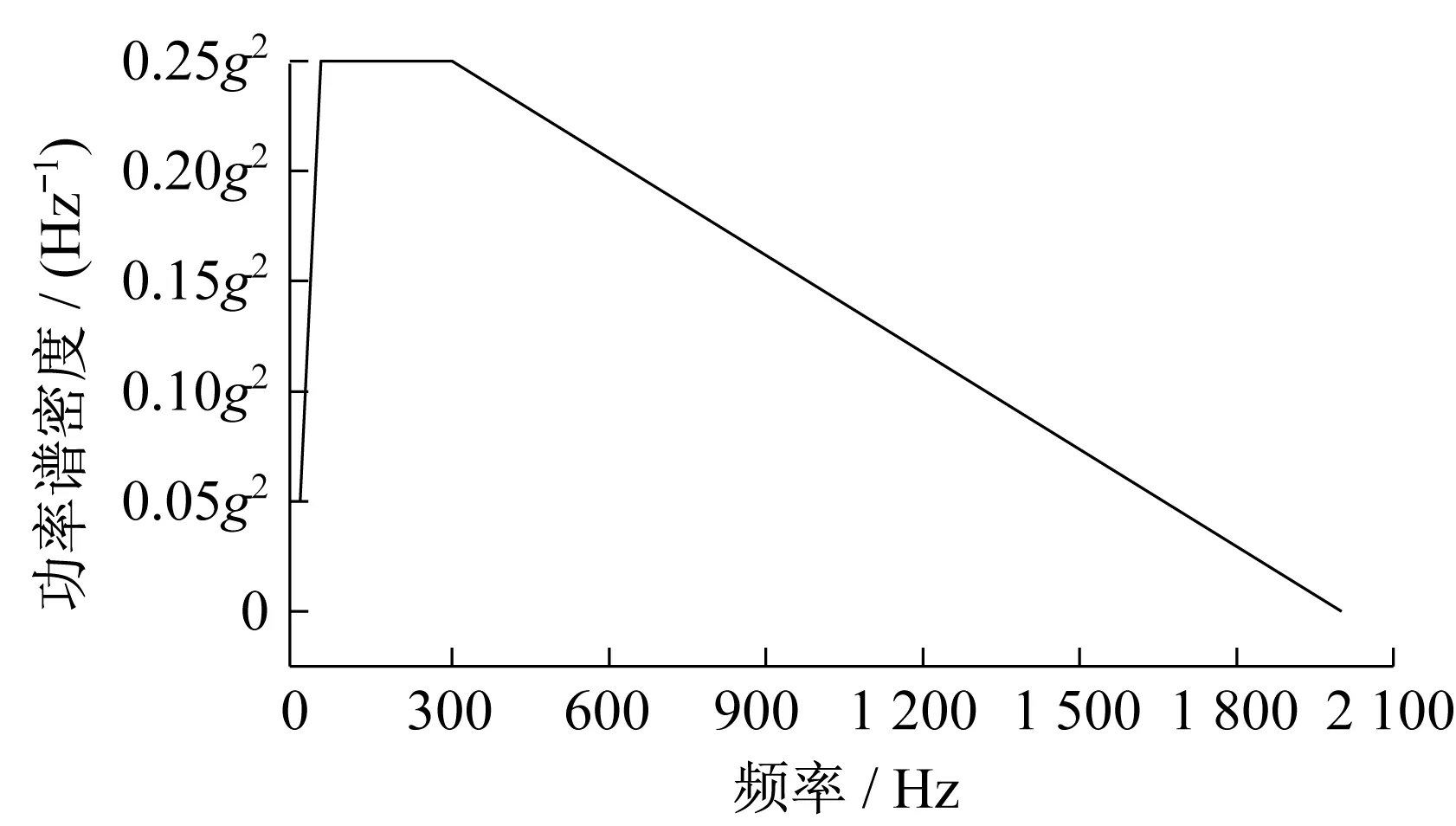
▲图5 随机振动激励曲线

4.3.4 冲击

冲击条件见表4。冲击激励施加在模型中的固定约束位置处,加载的方向包括X、Y和Z三个方向。

表4 冲击条件

表4中1 dB/oct的计算式为:

(4)

式中:A0为参考加速度有效值;A为相对于A0时的计算加速度有效值。

根据式(4)可以计算出100～650 Hz范围内不同频率下的冲击谱相应加速度。冲击的激励曲线如图6所示。

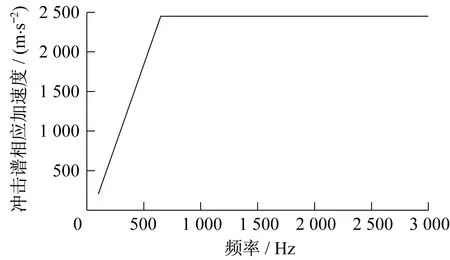
▲图6 冲击激励曲线

5 仿真结果

后支架所用材料为7075-T6铝合金,材料的密度为2 810 kg/m3,杨氏模量为72 GPa,屈服强度为505 MPa,泊松比为0.33。

5.1 加速度

加速度分析主要用于研究结构件在加速度载荷作用下的应力响应,笔者基于ANSYS Workbench软件中的结构静态分析模块,分析后支架在加速度条件下的应力响应。

通过分析,加速度载荷下后支架的最大等效应力为13.593 MPa,如图7所示。

▲图7 加速度载荷下后支架等效应力

5.2 模态

模态分析是进行正弦振动分析、随机振动分析和冲击分析的基础,为正弦振动、随机振动和冲击分析提供求解模态[6]。

笔者提取了前350阶系统模态,一阶模态频率为101.77 Hz,350阶模态频率为2 145.6 Hz,系统模态振型如图8所示。一阶模态频率高于100 Hz,即高于正弦振动的最高频率;350阶模态频率高于2 000 Hz,即高于随机振动的最高频率,满足求解要求。

▲图8 系统模态振型

5.3 正弦振动

基于ANSYS Workbench软件中的谐响应分析模块,分析后支架在正弦振动条件下的应力响应。

正弦振动激励频率范围为4～100 Hz,平均分为20段,常阻尼比设为0.05,采用模态叠加法进行计算。

正弦振动激励工况下,后支架在不同频率下的最大等效应力如图9所示。由图9可知,不同频率下后支架的最大等效应力曲线与正弦振动的加速度幅值曲线基本一致,等分越多,两曲线轮廓越接近。最大等效应力最大值产生于频率为71.2 Hz时,为64.46 MPa,如图10所示。

▲图9 不同频率下后支架最大等效应力

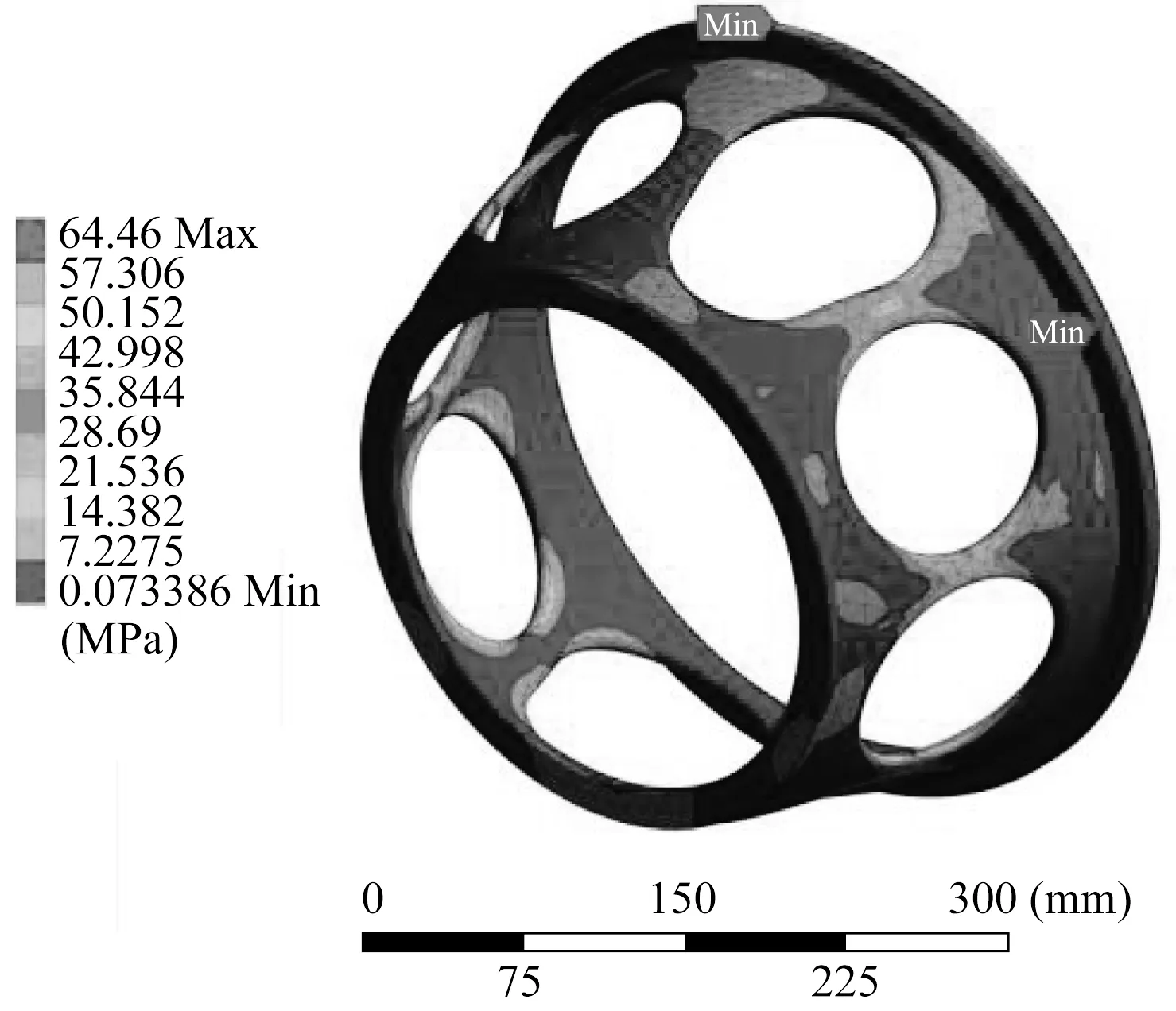
▲图10 频率71.2 Hz下后支架等效应力

5.4 随机振动

基于ANSYS Workbench软件中的随机振动分析模块,采用模态叠加法分析后支架在随机振动条件下的应力响应[7]。

68.269%概率[8]下的后支架等效应力如图11所示,最大等效应力为120.33 MPa。

▲图11 68.269%概率下后支架等效应力

5.5 冲击

基于ANSYS Workbench软件中的响应谱分析模块[9-10],采用模态叠加法分析后支架在冲击条件下的应力响应。

冲击载荷下后支架的等效应力如图12所示,最大等效应力为145.03 MPa。

▲图12 冲击载荷下后支架等效应力

5.6 结果分析

通过以上仿真得到后支架轻量化后在加速度、正弦振动、随机振动、冲击等不同载荷下的最大等效应力。结构安全裕度MS的计算公式为:

(5)

式中:[σ]为材料的屈服强度;σmax为结构的最大等效应力;k为安全因数,取1.25。

不同载荷下后支架的结构安全裕度见表5。

表5 不同载荷下后支架结构安全裕度

由表5可知,后支架轻量化后在加速度、正弦振动、随机振动、冲击等四种不同载荷下的结构安全裕度均大于零,表明后支架轻量化后结构安全,满足设计要求。

6 结束语

笔者采用有限元法分析了轻量化支架在加速度、正弦振动、随机振动、冲击等不同载荷下的结构等效应力,并计算了不同载荷下轻量化支架的结构安全裕度,结果表明轻量化支架结构安全,满足设计要求。笔者所做仿真可以为支架的轻量化设计提供参考。