锥齿轮传动机构的优化设计

□ 王远东 □ 高 洁

1.西安职业技术学院 西安 710077 2.陕西省图书馆 西安 710061

1 优化设计背景

锥齿轮的作用是传递两相交轴之间的运动和动力。与圆柱齿轮类似,锥齿轮有较多分类。按轮齿的外观,可以将锥齿轮分为直齿锥齿轮、斜齿锥齿轮、螺旋锥齿轮[1]。锥齿轮传动的优点在于传动效率高、传动比稳定、工作可靠、结构紧凑、节省空间、耐磨损、寿命长、噪声低。目前,锥齿轮传动在众多领域得到了广泛应用。当前锥齿轮传动优化设计的主要目标是在满足承载能力的条件下,选择合适的齿轮副参数,使传动装置的体积和最小,以及结构紧凑[2-4]。

目前,国内学者对锥齿轮传动的试验和研究较为深入。叶小芬等[5]将减速器尺寸和强度设计纳入约束条件,建立数学模型,利用Matlab优化工具箱进行结构优化设计,求解传动机构体积和最小目标函数。孙宏洁等[6]以齿轮模数和传动比等作为设计参数变量,将齿轮齿面和齿根强度要求与机构间不发生干涉作为约束条件,将齿轮副的传动总中心距最小作为目标函数,利用Matlab工具箱进行求解。李旭贞[7]将齿轮的参数整合为优化数学模型,结合粒子群优化算法进行目标函数的求解。以上研究均使齿轮副获得了较小的体积,但同时也存在一些弊端,不能满足齿轮传动的多目标优化要求,如齿轮副啮合的重合度不足、强度不高,导致齿轮传动的平稳性下降。

笔者建立锥齿轮传动机构优化数学模型,采用遗传算法和Matlab工具箱对目标函数进行求解。遗传算法模拟达尔文进化论的自然选择和遗传学机理,是一种不断选择优良个体的随机化搜索算法,直到在全局中搜索出最优个体。遗传算法以对较为复杂多峰函数的适用性和对目标函数的全局优化性等特征在工程优化设计中得到广泛应用,特别是在机构结构参数优化设计、生产调度、模式识别、神经网络、自适应控制等领域,遗传算法降低了多目标函数求解的难度,取得了显著效果[8-9]。

2 优化设计数学模型

在锥齿轮传动机构的优化设计中,以锥齿轮副的体积之和最小作为设计目标。

如图1所示,轴交角为90°的锥齿轮副主要结构尺寸包括分度圆直径d、锥齿轮副锥距R、锥齿轮宽度b、分度圆锥角δ等。

锥齿轮副的体积和V为:

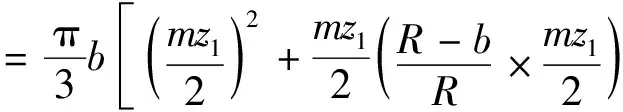
(1)

b=ψRR

(2)

(3)

式中:z1、z2分别为大小锥齿轮的齿数;m为锥齿轮副的大端模数;R为锥齿轮副的锥距;b为锥齿轮的宽度;ψR为齿宽因数;δ1、δ2分别为大小锥齿轮的分度圆锥角。

由式(1)可知,影响锥齿轮副体积和的参数有小锥齿轮的齿数z1、锥齿轮副的大端模数m、齿宽因数ψR,因此可将设计变量x设为:

x=(z1,m,ΨR)T=(x1,x2,x3)T

(4)

齿面接触强度条件为:

(5)

式中:[σH]为锥齿轮副的齿面许用接触应力;K为锥齿轮副的工作情况因数;T1为主动小锥齿轮传递的转矩;u为大小锥齿轮的齿数比,u=z2/z1。

齿根弯曲强度条件为

(6)

式中:[σF]为锥齿轮副的齿根许用弯曲应力;YFS为复合齿形因数。

对于复合齿形因数,可以根据当量齿数通过图2查取。

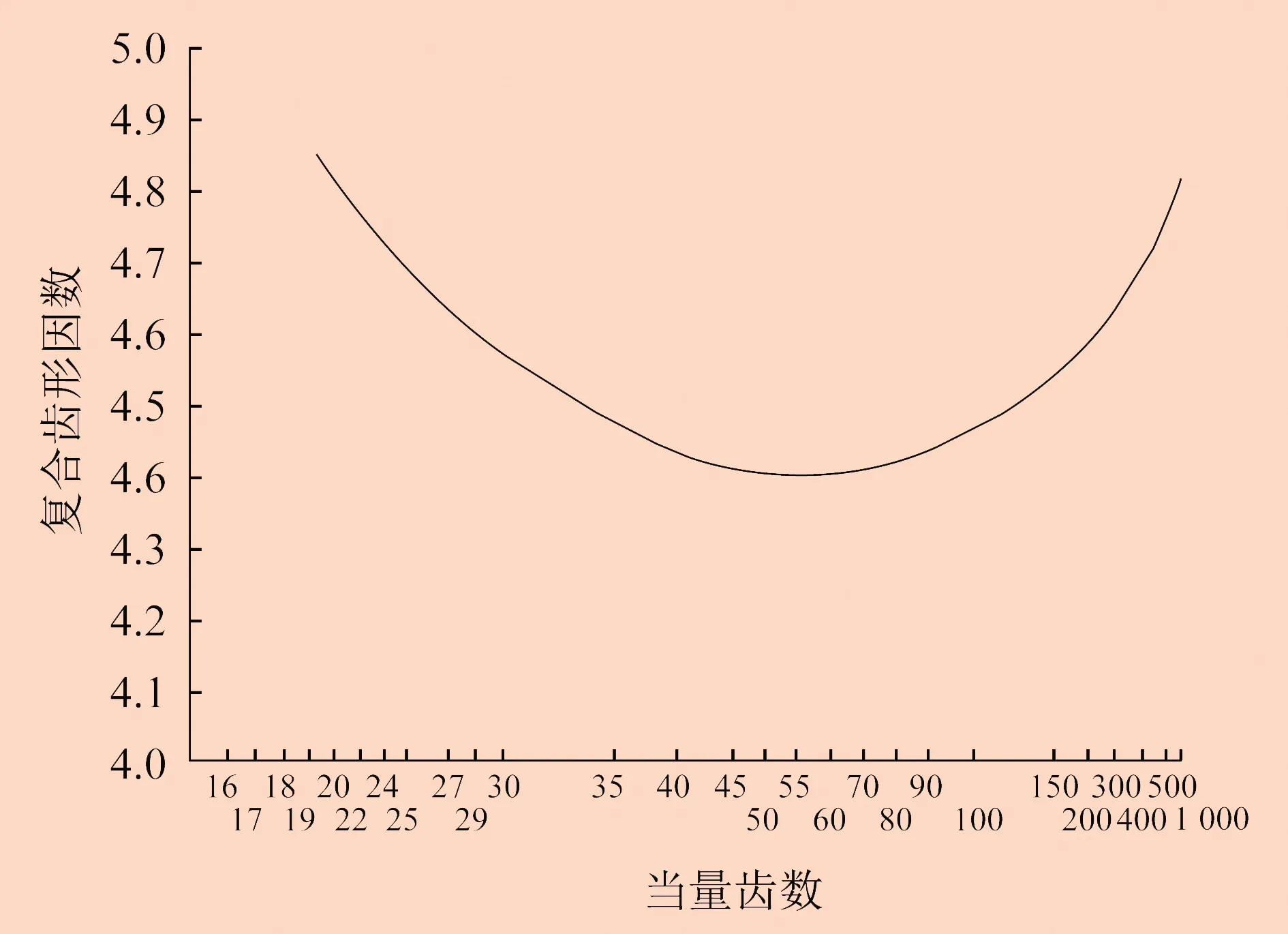
图2 复合齿形因数与当量齿数关系

设计变量的边界条件为:

17cosδ1≤z1≤z1max

m≥2

0.25≤ψR≤0.30

由以上数学模型可见,锥齿轮副体积和最小的优化设计可归纳为三维非线性约束优化问题。

3 优化设计实例

已知一汽车发动机传动机构是轴交角为90°的闭式锥齿轮传动机构,其中小锥齿轮传递的功率P1为9.2 kW,转速n1为970 r/min,传动比i为3,工作情况因数K为1.5。小锥齿轮的材料为40Cr,经过调质处理,布氏硬度(HB)为250。大锥齿轮的材料为35SiMn,调质处理,布氏硬度(HB)为230。要求以锥齿轮副体积和最小为目标进行优化设计。

对上述参数进行整理计算,可求得主动小锥齿轮工作时的转矩T1为:

T1=9 550P1/n1=90.6 N·m

根据锥齿轮传动机构的材料和金属工艺学规范,从文献[10]中查出齿面许用接触应力[σH]为640 MPa,齿根许用弯曲应力[σF]为250 MPa。

惩罚函数法是一种间接求解约束优化问题的方法,将约束优化问题转换为一系列无约束问题来求解,不破坏原有的约束条件[11]。笔者采用惩罚函数法中的外点法,将约束非线性规划问题构造为适应度函数val(x):

val(x)=f(x)+p(x)

(7)

式中:f(x)为数学模型的目标函数;p(x)为惩罚项。

对于极小化问题,有:

p(x)=0

或

p(x)=-r1[g1(x)]2-r2[g2(x)]2<0

(8)

式中:r1、r2为惩罚项因子,是随着迭代次数增加而递增的正数数列。

将式(8)中的三维不等式约束非线性目标问题转换为外点惩罚函数形式适应度函数问题,即将优化设计数学模型中式(5)、式(6)两个性能约束构造为适应度函数中的惩罚项,再将数学模型设计变量的边界条件作为遗传算法中的变量上下限矩阵。

本例中锥齿轮副是软齿面闭式齿轮传动,结合锥齿轮传动运算法则,取锥齿轮齿面接触强度条件的惩罚项因子r1为1,锥齿轮齿根弯曲强度条件的惩罚项因子r2为0.5。

由于主动小锥齿轮的齿数较少,在大多情况下复合齿形因数较大,因此应将复合齿形因数作为锥齿轮齿根弯曲强度条件计算的依据。本例中,复合齿形因数可取4.80。

运用Matlab优化工具箱fmincon函数,在主程序中输入分度圆直径、齿数比、锥距、齿宽、目标函数等数据。.m格式文件部分关键程序如下:

Function{sol,y}=GA_yzcl(sol,options)//定义适应度函数文件

z1=x(1);

m=x(2);

psi_R=x(3);

x(1)=sol(1);

x(2)=sol(2);

x(3)=sol(3);//设计变量

u=3;

d1=x(1)*x(2)/2;

d2=u*d1;

R=d1*sqrt(1+u^2);

b=x(3)*R;

sdelta1=x(1)*x(2)/(2*R);

cdelta1=sqrt(1-sdelta1^2);

sdelta2=u*sdelta1;

cdelta2=sqrt(1-sdelta2^2);

V1=cdelta1*(d1^2+d1*((R-b)*d1/R)+((R-b)*d1/R)^2)

V2=cdelta2*(d2^2+d2*((R-b)*d2/R)+((R-b)*d2/R)^2)

F=pi/3*b*(V1+V2);//目标函数

K=1.5;

P1=9.2;

n1=970;

T1=9550*P1/n1;

sigma_HP=640;

sigma_FP=250;

YFS=4.80;

g1=sigma_HP-sqrt((195.1/x(1)*x(2))^3*K*T1/u)

g2=sigma_FP-(3.2/x(2))^3*K*T1*YFS/(x(1)^2*sqrt(u^2+1);

r1=1;

r2=0.5;

p=r1*g1^2+r2*g2^2;

If(g1>=0&(g2>=0)

y=-f;

Else

y=-(f+p);//将不等式约束作为惩罚项加入适应度函数

End

主程序运行结果见表1。

表1 锥齿轮传动机构优化设计最优解

将最优解代入约束条件进行检验,g1(x)=-0.081 MPa≈0,g2(x)=247.591 1 MPa>0,可见最优解位于齿面接触强度条件的边界上,齿根弯曲强度则有很大富裕。

将最优解中的小齿轮齿数圆整为整数值19,再代入约束条件进行检验,g1(x0)=13.603 1 MPa>0，g2(x0)=247.659 5 MPa>0，可见最优凑整解位于可行域内。

4 结束语

笔者分析了锥齿轮传动机构的特征,对其建立数学模型,得到优化设计变量、目标函数,以及性能约束条件和边界约束条件,进行优化设计。采用惩罚函数法构造适应度函数,将优化设计数学模型中的齿面接触强度条件和齿根弯曲强度条件构造为适应度函数中的惩罚项。编制遗传算法.m格式文件,运用Matlab优化工具箱fmincon函数进行求解,得到最优解。程序运行结束后,还需要对设计变量进行圆整和调整。

通过优化实例验证了采用遗传算法进行锥齿轮传动机构优化设计的可行性和适用性,为锥齿轮传动机构的多目标优化设计提供了参考。