聚焦集合中常用的数学思想

张金娥

集合是学习数学的基础，是高考的必考内容。求解集合问题常用的数学思想有：数形结合思想，分类讨论思想，函数与方程思想，补集思想。

一、数形结合思想

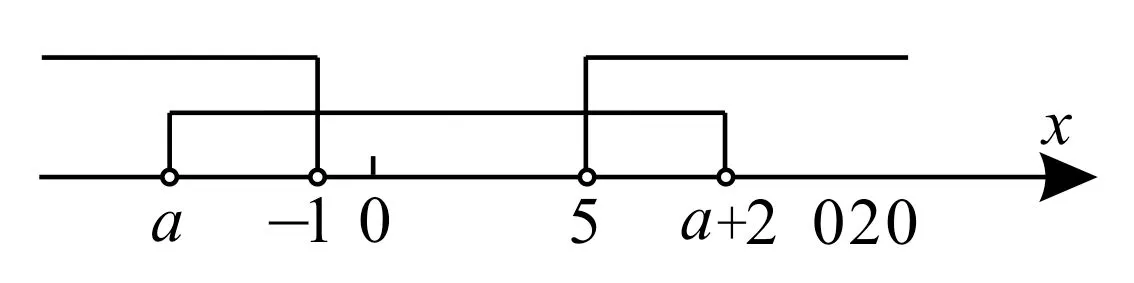
图1

评析：解答这类问题，先在数轴上表示集合，再利用题设条件，列出满足题意的不等式组，要特别注意等号是否成立的情况。

二、分类讨论思想

评析：解题时，分别列出关于实数a的不等式组，解出a的范围，再求并集得到结果。

三、函数与方程思想

评析：解题时，要注意集合元素的互异性。题中的集合都是三个元素，由两个集合相等，可知集合中元素完全相同。

四、补集思想