电动车电机悬置系统瞬态性能优化

裴宝浩， 于 蓬， 邢 勤， 周 娟， 张元元

（1.烟台职业学院，山东 烟台 264670；2.山东明宇新能源技术有限公司，山东 济南 271100；3.新兴交通建设有限公司，山东 烟台 264000；4.淄博职业学院，山东 淄博 255314）

纯电动汽车的驱动电机具有快速响应特性，一方面使电动车比传统车有更好的加速性能，另一方面也使电机悬置系统产生相对的冲击和振动较大。

目前国内针对电机动力总成悬置系统的研究已经取得了初步的进展。2006～2010年间，同济大学的一些学者对电机动力总成悬置系统进行了初步研究，并探索改善瞬态工况下悬置系统的振动响应问题［1-2］。2011年，辽宁工业大学的李莹探索了提高解耦率对电机动力总成悬置系统隔振性能的影响［3］。在国外，尽管许多科研院所和各大汽车公司都进行了电动汽车的研发，出于技术保密或其它原因，电驱动动力总成悬置系统的研究文献并未公开发表，较难阅见。

本文结合某电动车的瞬态振动问题进行其动力总成悬置系统的仿真和优化研究。

1 利用ADAMS进行电机悬置系统建模和仿真分析

1.1 动力学仿真模型的建立

该系统由3部分组成，分别为电机、减速器和3个橡胶悬置，一般对悬置系统的隔振性能进行研究时往往将其简化为6自由度的刚体模型，将橡胶元件简化为3向正交的弹簧阻尼模型［4］。

在ADAMS／View中导入用CATIA建成的电机模型，如图1所示。

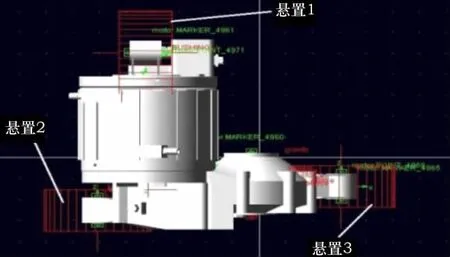
图1 ADAMS中电动车电机模型

1.2 系统模型仿真分析

电机悬置系统的固有频率极其重要，鉴于系统的简化模型，一般其各个自由度方向的振动不是没有联系的，而是存在着相互耦合，即某一个方向上受到激励，在整个系统上会产生多个方向的振动，这将导致系统振动时的振幅增大，频带加宽［5］。

由于耦合作用的存在，一方面会加宽系统振动的频带，另一方面也会在隔振以及频率的配置方面带来不小的困难。基于以上原因，在实际工程中，采取降低和控制系统的振动解耦是解决电机悬置系统振动耦合的方法，效果较为显著，并且被普遍采用。本文利用电机悬置系统的6自由度模型，来分析系统的耦合特性［6］。通常情况利用振动时的能力分布来表示其耦合特性。

在工程实际设计中，系统的解耦率基本无法达到100%，当解耦率达到或者超过90%时，通常认为系统达到解耦目标，对于电机悬置系统子模型，根据ADAMS／Vibration模块的仿真结果获得电动车电机悬置系统的能量分布，其频率和解耦率如表1所示。

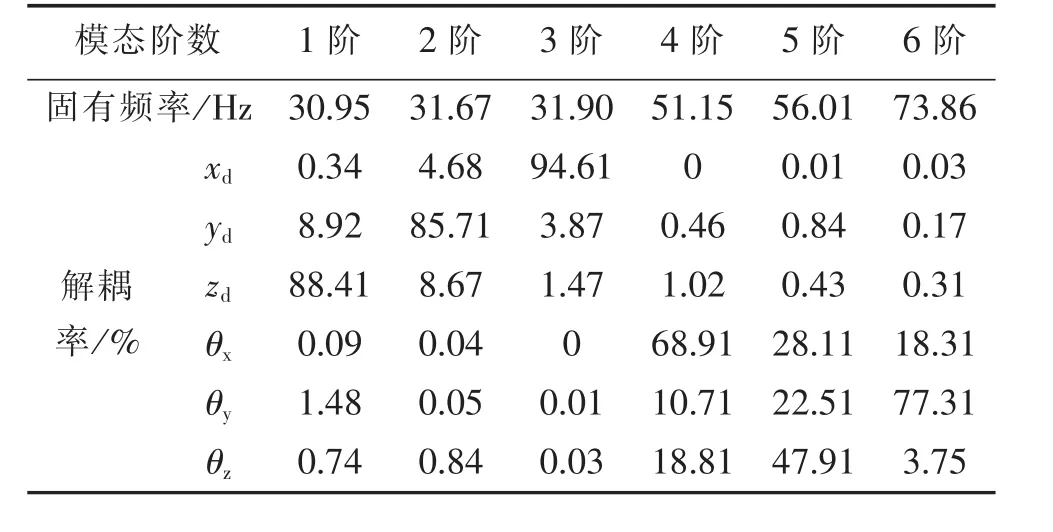
表1 电机系统的固有频率及解耦率

在各阶模态振动下，悬置系统的能量分布较为分散。最集中自由度能量发生在第1阶和第3阶，分别为88.44%和94.61%，最低的解耦率仅有47.98%，而其余各阶也均较低。这说明动力总成悬置系统的耦合比较严重，各个方向的激励对其他方向的振动有很大的影响，加剧了系统的振动，该动力总成悬置系统设计欠合理。

1.3 加速和制动工况下阶跃转矩响应分析

电动汽车的电机不同于传统的内燃机，其在没有转速的情况下也能提供并输出较大的转矩，而且电机能够提供很快的响应速度，即电机的输出转矩能够在极短的时间内提供较大转矩变化范围。但是在实际工作中发现，电动车的电机系统在两种工况下振动表现得非常明显，甚至很严重，就是在电动车急加速工况和紧急制动工况时表现出来。

基于以上分析，利用ADAMS／View对电机悬置系统在急加速和急减速两种工况下仿真，并分析计算其在两种工况下10s内的瞬态响应。起步急加速工况时，电机的最大驱动力矩为120Nm，在乘以传动比 （i=7.25）后作用于动力总成的驱动力矩为870Nm，而紧急制动工况时设汽车的制动减速度为0.8g，并按照前后制动力的分配关系转化成前后轮的制动扭矩，计算后得到制动力矩为580Nm，电机响应时间取1ms。仿真结果见图2～图4。

由仿真结果图2～图4中可以看出，在刚开始的时间里，即电动车急加速工况的起始阶段系统的瞬态振动情况，在此过程中系统的振动幅度较大，随后曲线慢慢稳定。在制动过程中，制动的起始阶段系统曲线再次由稳定状态变成瞬态阶段，同样在瞬态的起始阶段曲线幅度较大，随之慢慢稳定趋于直线。这个过程与车辆的实际情况相符合，即车辆起步阶段和减速阶段的初期，电机悬置系统由稳态变化进入瞬态，然后又将回复保持到稳态的情况。

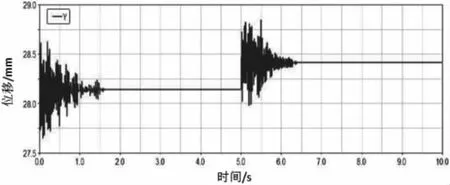
图2 优化前电机总成Y方向的位移

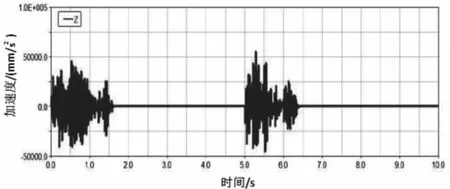
图3 优化前电机总成的Z向加速度

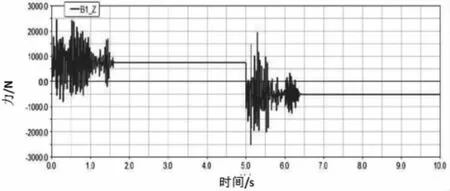
图4 优化前悬置元件1的Z向动反力

3个橡胶悬置元件的Z向受力和变形都比较大，最大值达到12800N，最大位移达到13.2mm，在制动过程中悬置元件的力和变形都有较大的变化。在这个过程中，系统容易发生运动干涉，而且由此可能会引起元件的疲劳损伤。

2 系统优化

1）目标：本文对系统的优化目标是能量解耦率。为了能够使系统在各个自由度方向达到尽可能最优的解耦，只能通过设计合理的参数来实现。

2）变量：参照以往的优化，系统的两个参数，质量、惯性不进行修改；阻尼的作用主要是为了降低共振的峰值，虽然其对系统的振动能够产生较大的影响，但是本文亦不作为变量，采用的是固定阻尼比；鉴于安装控件狭小，橡胶元件的位置和校对安装能够改变的可能性极小；因此结合各种因素的分析，变量设定为橡胶元件的刚度参数，以此来进行优化解耦。

3）约束：为了防止共振现象的发生，根据隔振理论，该电机橡胶悬置系统的1阶固有频率应该大于其车身和座椅的固有频率，至少为倍。

以该款电动车的电机悬置系统为对象，利用ADAMS参数化优化模块进行优化分析。经过ADAMS的优化计算，得到橡胶元件的刚度参数如表2所示。优化后的固有频率和解耦率如表3所示。

表2 橡胶悬置元件在优化前／后的刚度

表3 优化后悬置系统固有频率及解耦率

从表2和表3可知，优化前后固有频率的值也发生了较大变化，原先第1、2、3阶频率均在31Hz左右，由于频率值相距太近，无法满足不同阶次间固有频率至少相距1Hz的要求，经过优化后，各阶固有频率均有明显差距，而且能量解耦情况得到了显著改善，特别是对于电动汽车动力总成悬置系统非常关键的θy方向的解耦率达到了98.94%，其他方向的解耦率也都超过或者接近90%，满足了工程上解耦的要求［8］。

3 优化后悬置系统的动态响应

将优化后悬置系统中的悬置元件刚度替换优化前的刚度，继续在ADAMS／View中进行动态响应仿真分析，得到优化后的各悬置位移、振动加速度、动反力以及动力总成质心3向振动位移的幅值及响应曲线。具体仿真结果见图5～图7和表4～表7。

优化后，悬置系统瞬态响应较差方向Z向的振动得到了明显改善，无论是位移还是动反力，幅值都有所下降，除了起步工况的X向位移，两种工况下动力总成质心的3向振动位移幅值都明显减小，其中制动时Y向质心位移的降低最为明显，减小了接近40%。

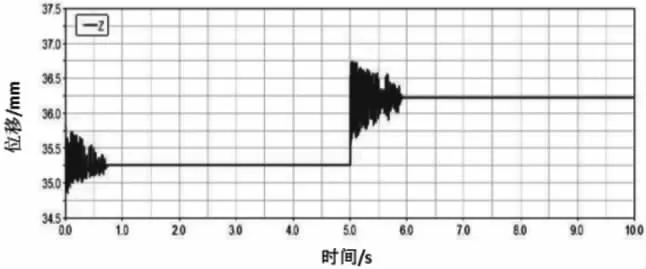
图5 优化后总成质心X向位移

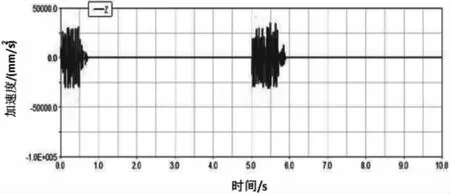
图6 优化后总成质心Z向加速度

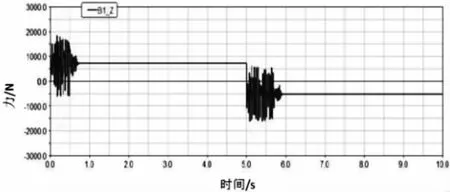
图7 优化后悬置1的Z向动反力

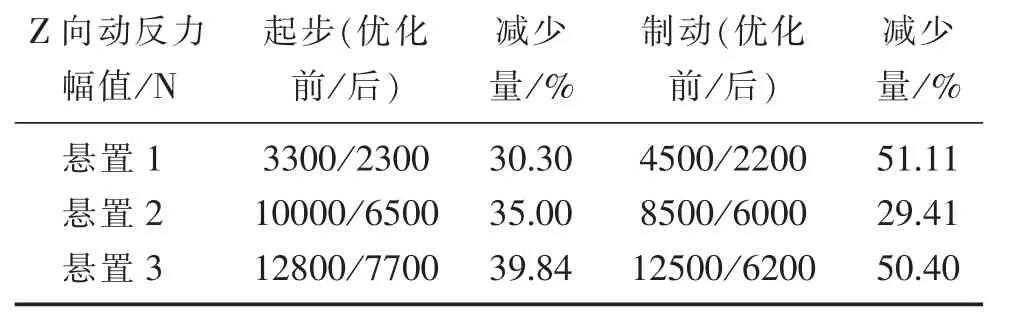
表4 优化前后各悬置Z向动反力幅值对比

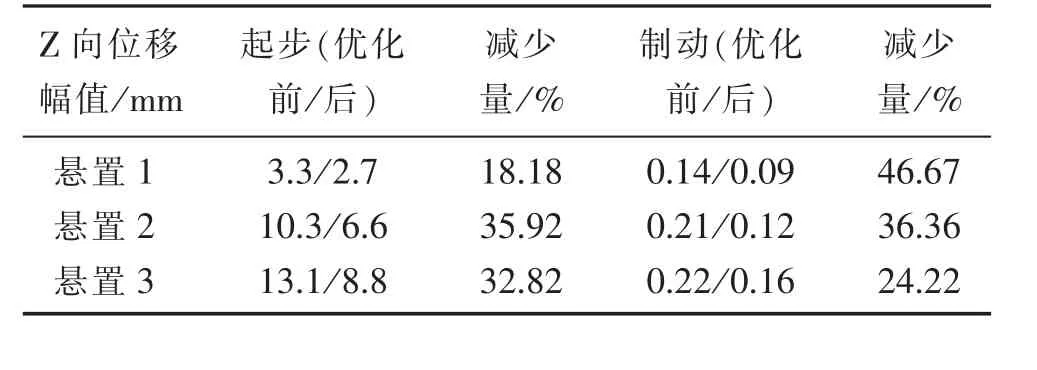
表5 优化前后各悬置Z向位移幅值对比

表6 动力总成质心3向振动位移幅值对比

表7 动力总成质心Z向加速度幅值对比

优化后，驱动和制动工况下，3个橡胶悬置元件Z向受力情况得到明显改善，力的峰值和幅值都有所降低。起步急加速工况的Z向动反力幅值均降低超过30%，而紧急制动工况下悬置1和悬置3的减小量甚至超过了50%。同时，两种工况下，电机悬置系统元件很快衰减了其振动，与此同时整个系统的NVH性能得以提高。

4 总结

本文利用ADAMS对该电动车的电机悬置系统进行了建模、仿真和分析，并对系统进行了优化设计，通过仿真分析和优化，使悬置系统的隔振性能得到了改善。悬置系统元件优化后，通过结果可以看出改善了系统的固有特性并且较大地提高了系统各个方向的解耦率，使其满足了工程要求。