地面层自适应光学系统多颗激光导引星位置优化研究

李彩凤，贾 鹏,2,3*，蔡冬梅

1太原理工大学物理与光电工程学院，山西 太原 030024；

2新型传感器与智能控制教育部(山西省)重点实验室，山西 太原030024；

3杜伦大学高等仪器研究中心，英国 杜伦 DH1 3LE

1 引 言

大气湍流对光束传输的扰动，严重影响了地基望远镜的观测能力。不同台址多年实测的湍流数据表明：越接近地面，大气湍流强度越强，其对来自天体光波的扰动也越大[1]。为此，科学家提出了地面层自适应光学系统的概念(GLAO)[2]：通过多个激光导引星和波前探测器对地面层大气湍流造成的波前畸变进行测量，之后利用一个变形镜校正地面层大气湍流的影响，进而可在较大的视场内适度提高地基望远镜的观测能力[3-4]。为保证有效的观测视场，地面层自适应光学系统多采用多颗激光导引星作为参考目标。考虑到激光产生与发射系统复杂且价格昂贵，多数地面层自适应光学系统仅使用3～5颗激光导引星[5-7]。

激光导引星的位置排布对地面层自适应光学的系统性能会有一定影响。其最优排布位置与很多参数有关，其中大气湍流强度随高度的分布函数(大气湍流强度廓线)是影响导引星位置的主要因素[8]。大气湍流是一种在空间和时间上随机变化的介质[9]，该特性使同一台址下的廓线变化具有一定随机性。随机变化的湍流廓线必然会对地面层自适应光学系统性能带来影响，因此在导引星数目有限的情况下，从统计意义上分析不同大气湍流强度廓线对应的导引星优化位置分布很有必要。当前地面层自适应光学系统中，多采用蒙特卡洛模拟法，在典型大气湍流模型下通过计算系统的性能，得到多颗激光导引星的排布方式[10-12]。由于大气湍流廓线具有随机分布的特性，分析不同实测湍流廓线下的导引星位置需要计算不同廓线对应的位置。此时，利用蒙特卡洛法需要计算大量不同的湍流强度廓线对应的地面层自适应光学系统性能，这会耗费极多的计算资源。

因此，本文针对大量实测的大气湍流廓线数据提出了一种导引星优化方案，首先引入一个简化的地面层自适应光学系统几何模型[13]，在该模型基础上使用遗传算法作为寻找导引星位置的优化算法，并且采用多进程、Numba库和多线程对上述两个过程进行加速处理，通过上述方法可以方便快速地分析实测湍流数据对应的导引星最优位置情况。

2 地面层自适应光学系统性能评估的简化几何模型

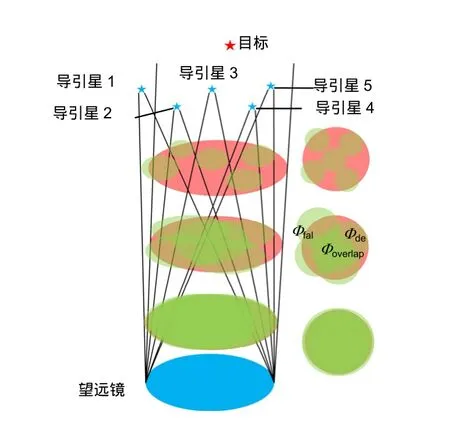
激光导引星的位置排布主要会影响地面层大气湍流的测量和重建结果，为快速估计不同导引星分布下的地面层自适应光学系统性能，本文采用一个仅考虑导引星发出的光波对地面层大气湍流采样能力的简化模型[13]。由于本模型采用了归一化的大气折射率结构常数系数，同时假设变形镜具有完美的校正能力，因此仅用于在视场确定、导引星数目确定的情况下，对导引星排布进行快速优化。模型将大气湍流等效为多层分布于不同高度的薄相位屏，如图1所示。其中科学目标处于无穷远，激光导引星处于有限高度。来自科学目标的光波所经历的大气湍流路径近似为柱状，而导引星的光波所经历的大气湍流路径为圆锥状。科学目标在每一层大气湍流截出一个和望远镜口径大小相同的圆形，而导引星截出一个半径随高度减小的圆形。

WF(the fraction of the wavefront)为激光导引星光束所采样的湍流信息占科学目标光束所经历的湍流信息的百分比(为了简写方便，用Φ表示)。如图1所示，多个激光导引星光波在每层的采样结果由三部分组成：位于科学目标光束路径之外的Φfal、在科学目标光束路径上由多个导引星共同采样的Φoverlap以及在科学目标光束路径上每个导引星各自独立采样的Φde。只有当激光导引星所采样的湍流信息与科学目标光束所经历的湍流重叠时，其测量结果才是有效的(根据这一校正结果，可以有效地提高科学目标信噪比)。定义激光导引星光束与科学目标光束重叠区域内的Φ为1。由于大气湍流相位分布是连续的，因此位于激光导引星光束和科学目标光束重叠区域之外的Φ对系统校正也有一定作用，可用下式表示：

其中：r0是大气相干长度，d是激光导引星在科学目标光束路径之外与路径之内最近采样点之间的距离，b是一个由相干长度r0和大气湍流的外尺度L0决定的常量。当d大于或等于大气湍流的外尺寸L0时，激光导引星在科学目标光束路径上的采样几乎没有任何贡献，则设置WF为-1。此时，可以由给定的r0和L0计算出b。本文将参数r0设为0.1 m，L0设为10 m(实际使用中，可以根据具体测量参数进行修改)。

在高度为h的大气湍流层，设该层的WF为Φ(h)，即：

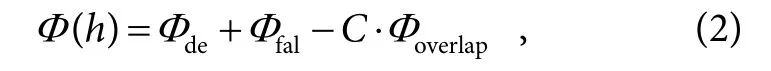
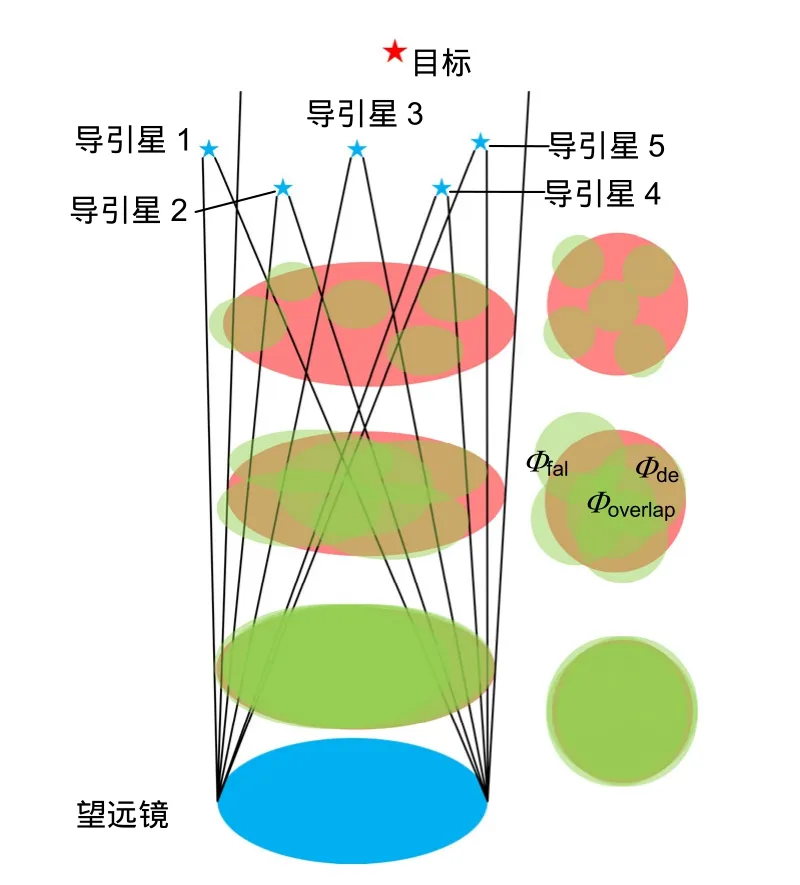
图1 地面层自适应光学系统简化几何模型图Fig.1 Geometric model for ground layer adaptive optics systems

其中：Φde、Φfal分别为N个激光导引星各自在该层目标区域之内和区域之外产生的 WF之和，Φoverlap为所有导引星在目标区域之内重叠产生的WF之和。C为多颗激光导引星同时采样同一位置波面时，每颗导引星对波前测量的贡献度。本文假设多颗导引星同时采样同一个区域时，波前测量结果对于系统校正的最低贡献将减半，则将C设为50%。Φde、Φfal、Φoverlap分别表示为

其中：N为激光导引星数目，A(h)为激光导引星光束在该层投影的面积πr2，r可以利用相似三角形公式快速算出。由于本文着重讨论不同廓线下的导引星位置优化，为去除不同视宁度对计算结果的影响，我们将大气折射率结构常数进行归一化处理。最终以为权重，通过加权求和计算大气湍流对系统的整体性能Φsys(h)，计算式：

最后，考虑不同视场所对应的观测区域大小不同，根据视场不同位置采样点对应的面积作为权重求和，计算出地面层自适应光学系统的整体性能，计算公式如(7)所示。

其中：rn代表采样点到视场中心的角距离，M为所有的采样点数目。

对一个具体的地面层自适应光学系统来说，该简化模型计算出的系统相对性能差异可以直接用来确定导引星的最优位置。

3 导引星位置优化算法

大气是一种连续随机介质，其湍流廓线分布与台址和气候环境息息相关。对某一处特定的台址，可以对该台址的海量湍流廓线数据进行随机抽样，结合地面层自适应光学系统模型，通过数值优化的方法获取湍流廓线和导引星最优分布之间的映射关系。

3.1 大气湍流数据来源与处理

对传统地面层自适应光学系统或者多层共轭自适应光学系统的性能进行估算，目前多采用一个统计平均的大气湍流廓线作为典型廓线，但其并不能真正反映出具体台址的特征。尤其当湍流廓线的统计分布不满足高斯分布时，统计平均值给出的结果估计和实际系统的性能差距较大。为更好地评估实际大气湍流廓线对激光导引星位置的布局影响，本文使用两组实测台址数据作为湍流廓线数据库[14-15]进行研究。如表 1所示，一组是杜伦大学高等仪器研究中心(CFAI)用Stereo-SCIDAR[16]方法在智利帕拉纳尔观测台址下获取的2016年～2018年共7563条数据，该方法的高度空间分辨率较高，约为150 m左右，可以测量地面层湍流廓线。另一组是三十米望远镜选址团队(TMT)用MASS方法[17]在夏威夷莫纳克亚山观测台址下获取的2005年～2008年共计163208条数据，该方法的高度空间分辨率比较低，一般只给出指定高度的大气湍流廓线数据，本文用到的典型高度为0.5 km、1 km、2 km、4 km、8 km和16 km。

帕拉纳尔的湍流廓线数据格式如表2所示。根据地面层自适应光学系统简化几何模型，只需考虑随湍流高度变化的对系统的影响。湍流廓线数据从近地面开始，每间隔250 m采样获取，仪器所能测量的最大高度在25 km左右，由此将湍流廓线定义成一个包含100层薄相位屏的模型，对于一些测量值不足100层的湍流廓线数据在高空处补零。测量值的数量级在10-14到10-19之间，为计算方便，将进行标准化：先对其取对数 log10(为防止高空处部分值为零造成的对数运算为负无穷大，可将加1之后进行对数运算)，最后将结果映射到[0, 1]之间为大小100×1的矢量，标准化公式见式(8)和式(9)。由于本文关注的是地面层自适应光学系统的相对性能变化(而非绝对校正能力)，上述变换可以减少数据差异对计算造成的不便，并不影响不同导引星排布的相对结果差异。

莫纳克亚山观测台址下的湍流数据格式如表3所示：分别是将廓线分解为三层或六层的数据。本文采用六层大气湍流廓线数据，对应高度分别为0.5 km、1 km、2 km、4 km、8 km、16 km，的数量级在10-14到 10-24之间。这组数据中没有为零的，可直接根据式(10)进行标准化，这里为大小6×1的矢量。

3.2 基于遗传算法的导引星布局优化

湍流廓线和导引星的优化分布之间的映射是一个复杂的函数，难以利用常规的凸优化方法求解。本文将其视为一般的非线性优化问题，利用迭代思想尽可能地逼近最优解。提出采用遗传算法[18-19]获取导引星分布，主要原因是：1) 遗传算法直接对导引星位置坐标进行相关操作，其目标函数Φall(h)可以是任意的，无需要求计算Φall(h)的过程是离散的或连续的。2) 遗传算法本身按照概率进行优化，不需要特定的条件就能自动获取和指导优化导引星位置坐标的搜索空间,可以自适应调整搜索方向。3) 导引星位置坐标在优化过程中用概率性传递规则代替确定性规则的重组变异各态历经性，能够使导引星位置坐标具有更好的全局优化解。

表1 大气湍流数据情况Table 1 Atmospheric turbulence data

表2 帕拉纳尔台址下的湍流数据格式Table 2 Turbulence data format in paranal

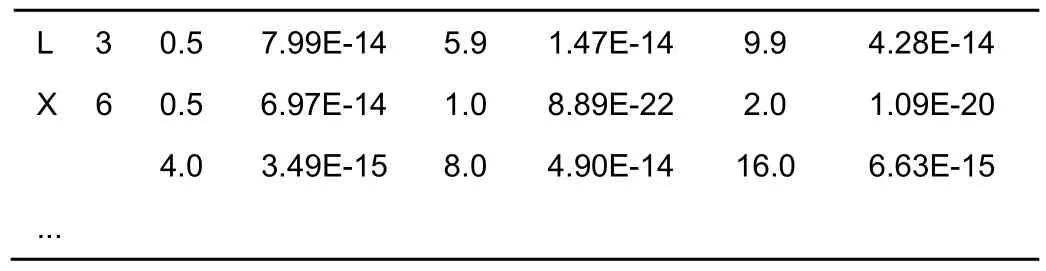
表3 莫纳克亚山台址下的湍流数据格式Table 3 Turbulence data format in Mauna Kea

本文针对一个口径为10 m，视场为14′的地面层自适应光学系统，首先考虑5颗导引星的情况，表4为地面层自适应光学系统参数。导引星位置采用极坐标(ρ，θ)表示，其中坐标原点为视场中心，极径ρ为视场方向上的位置，θ为圆周方向上的位置。ρ的取值范围为半视场角，即[0″, 420″]；θ的取值范围为整个圆周角，即[0o, 360o]，则遗传算法的搜索区域为一个半径420″的圆域，具体计算流程图如图2所示。

表4 地面层自适应光学系统的参数Table 4 Parameters of the ground layer adaptive optical system

3.2.1 初始化种群

将导引星坐标和坐标的边界范围初始化一个2×10的区域矩阵B，第一行为坐标上界，第二行为坐标下界，10列依次为坐标位置(x,y)，具体格式：

以B为限制条件，按整数值编码的方式创建种群矩阵G，其中Nind代表导引星坐标组数，Lind代表导引星对应的变量个数。

式(12)中，矩阵的每一行代表一组导引星位置坐标，坐标由随机的十进制整数构成，每个坐标就是对应变量的实际值。

3.2.2 导引星位置数据的重组和变异

导引星位置数据的重组选择减少代理的两点交叉方式，过程如图3所示，父代双亲染色体中的基因[a、b、c、d、e、f、g、h、i、j]、[A、B、C、d、e、F、G、H、I、J]分别对应两组导引星的坐标值，按照0.9的重组概率随机选中两个交叉点，该方式可以控制交叉点只出现在上一轮两个坐标不同的位置之间，避免子代中产生和父代相同的坐标。

导引星位置数据的变异方式采用实值突变，同时为了避免变异过程中使解陷入局部最优解，变异概率不宜太大，本文选为0.1，其变异示意图如图4所示，图中共有三个坐标值发生了变异，将变异后的坐标重新作为下一轮的父代坐标。

图2 遗传算法流程图Fig.2 Flow chart of the genetic algorithm

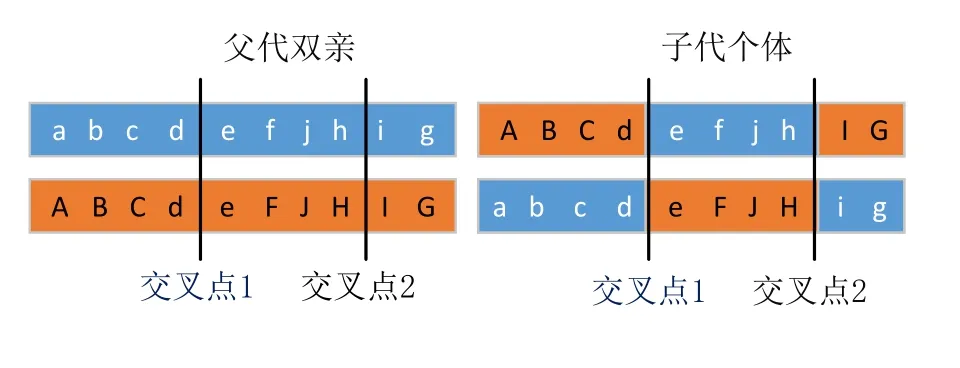
图3 遗传算法中染色体的重组过程Fig.3 Chromosome recombination process in the genetic algorithm

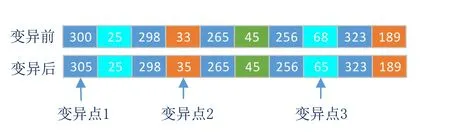
图4 遗传算法中染色体的变异过程Fig.4 Chromosome variation process in the genetic algorithm

3.2.3 适应度计算

本文采用等级划分的分配方式计算适应度，见式(13)。该方式根据Φall(h)的值从大到小对导引星坐标排序，然后根据坐标在排序中的位置来确定其适应度。

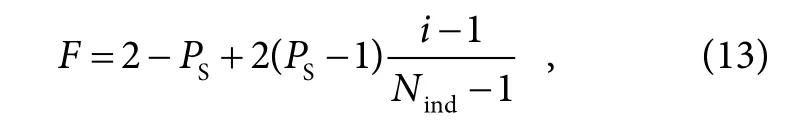
式中：PS为选择压力，决定种群的收敛速度，其取值必须在[1, 2]之间，本文选为2，Nind为导引星坐标的组数，i为每组坐标在种群中的位置。

3.2.4 导引星位置数据的选择

进化中的导引星位置用锦标赛式的方法进行选择，该方法模仿淘汰赛制，每次从种群中挑选出适应度最好的一组加入被选集合，重复该操作直到挑出0.5×Nind组新坐标作为子代，然后将选出来的个体和父代合并进行下一次的进化，每个个体i被选中的概率为P(i)为

3.2.5 子种群数目

图5 遗传算法中不同子种群数目的收敛效果Fig.5 Convergence effect of different subpopulations

子种群数目的多少与最优解的结果和计算时间息息相关。图5表示了不同子种群数目迭代了100次的收敛情况，图中不同颜色曲线依次代表子种群数目为20，30，40，50，100，不同数目的计算在 60代附近都达到收敛状态。虽然子种群数目越多，信息增益越大，但是运算时间也越长。本文主要考虑多个廓线下导引星的统计最优位置，信息增益的微小的差异可以忽略不记。所以最终选用的子种群数目为20。

3.3 计算时间加速过程

与蒙特卡洛法模拟相比，采用地面层自适应光学系统简化几何模型的计算速度得到了提升。但作为遗传算法中需要不断迭代优化的目标函数，其运行时间仍然较长(子种群数为1时，计算一条廓线下的地面层自适应光学系统性能需要近1 h)。

如果遗传算法迭代50次获得导引星最优值，对单个廓线而言，至少需要两天的时间，所以迫切需要提高整个过程的运算速度。

本文采用多进程、多线程和具有高性能计算能力的Numba库，分别对几何模型中计算量较大的模块和遗传算法子种群中多个独立个体部分进行并行处理。表5列出了研究过程中在算法不同部位的加速方法以及不同数目子种群个体下的运行时间。从表中可以看出，在几何模型中使用多线程，遗传算法中使用多进程的加速方法效果最有效(子种群个体为20时，加速比可达到3240：1)。

4 实验结果与分析

利用遗传算法，本文分别对不同实测台址廓线下的导引星位置，以及同一台址湍流廓线下不同数目的导引星位置做优化。

4.1 单条湍流廓线数据下的导引星位置优化分析

首先在帕拉纳尔观测台址下随机选取一条大气湍流廓线数据，用表1的地面层自适应光学系统参数，通过遗传算法计算5次该廓线数据对应的导引星最优位置，结果如图6所示。图6(a)～6(e)依次是5次的位置结果，图6(f)是5次总体结果，以下各图均用极坐标表示，其中极径为导引星半视场角上的位置，极角为圆周角上的位置。从计算结果可以看出，遗传算法算出的导引星位置在径向视场角的位置均为 320″(5.3′)左右，由于没有考虑风向的原因使角向圆周角的位置每次有所区别。

图6 一条湍流廓线数据下5次激光导引星位置结果。(a)～(e) 分别为5次相同条件下的导引星位置结果；(f) 5次位置的统计结果Fig.6 The position results of the laser guiding star for five measurements with single turbulent profile data.(a)～(e) The results of guiding star positions under the same condition for five measurements respectively; (f) Total positional results of five measurements

表5 不同加速方案的运行时间结果对比Table 5 Comparison of running time with different acceleration schemes s

选取另一条大气湍流廓线数据计算其对应的导引星最优位置分布，经过多次计算，该廓线下导引星的优化位置都在视场正中心。图7(a)～7(c)是选取3次的位置结果图，该结果证明了遗传算法计算同一个廓线最优位置时结果具有收敛一致性。

进一步分析上述两种位置排布不同的原因，图8(a)和8(b)分别画出了导引星位置呈正多边形和视场中心分布对应的大气湍流廓线，图中横坐标是标准化之后的对数坐标，纵坐标为湍流高度，从图中可以看出导引星位置分布为规则正多边形，对应的湍流强度集中在中底层，而导引星位置分布于视场中心时，湍流强度主要在中高层。由图1可知，与无限远处目标接近于平行光的传输路径不同，单个导引星测量的只是一定高度上到达望远镜口径的锥形路径上的波前畸变，高度和路径之外的大气湍流造成的波前畸变无法获得。当地面层大气湍流较强时，分散多颗导引星的排布可以保证校正整个视场内的科学目标图像质量。而当地面层湍流强度较弱时，高层大气对科学目标影响严重，多颗导引星分散分布会导致对不同视场的科学目标测量差异较大，因此导引星的位置分布更集中是一个相对稳妥的选择。另外，由于本论文提出模型更关注地面层自适应光学系统的相对性能，而非绝对性能。因此，目前尚无法衡量地面层湍流较弱时，地面层自适应光学系统的绝对性能如何。但是，从导引星排布情况大致能发现，当优化结果出现如图7所示情况时，将可能伴随地面层自适应光学系统性能下降的情况。

图7 另一条湍流廓线数据下3次激光导引星位置结果。(a)～(c) 分别为3次相同条件下的导引星位置结果Fig.7 The position results of the laser guiding star for three measurements with another turbulent profile data.(a)～(c) The results of guiding star positions under the same condition for three measurements respectively

图8 上述两种情形中对应的大气湍流廓线图。(a) 图6对应的大气湍流廓线图；(b) 图7对应的大气湍流廓线图Fig.8 Atmospheric turbulence profiles corresponding to the above two cases.(a) Atmospheric turbulence profile corresponding to Figure 6;(b) Atmospheric turbulence profile corresponding to Figure 7

4.2 多条湍流廓线数据下的导引星位置优化分析

为了具体分析不同实测台址下湍流廓线与导引星位置的分布关系，本文从统计角度考虑，在获取的全部湍流中随机采样 2000条帕拉纳尔和纳克亚山观测台址下的廓线数据，用遗传算法计算实测湍流廓线下导引星的最优位置。在湍流廓线到导引星位置这个映射空间内，每条湍流廓线之间彼此相互独立，而且随机采样过程中每个样本都服从同一个分布。机器学习理论指出服从独立同分布(i.i.d)的每个随机变量有着相同的分布形状和分布参数，即采样获得的湍流数据和该台址下对应的所有湍流数据有着相同的分布特征。所以，在随机采样的湍流数据下计算出的导引星位置，可以反映出该台址下所有湍流廓线与其导引星位置分布的关系。

图9(a)和 9(b)分别是两个观测台址在采样湍流数据下，用遗传算法多次计算得到的位置统计密度图，图中每个点代表一个导引星，颜色越深表示落在该位置的导引星数目越多。可以看出，两个观测台址下导引星位置集中分布的具体形状是不同的，但是均服从边缘呈正多边形以及中心一颗的规律。此计算结果表明，相比根据典型湍流模型计算出一致的导引星位置排布，本文提出的优化方案可以根据不同实测场景计算不同的导引星排布更有研究意义。

此外，发现帕拉纳尔的导引星位置分布更接近于规则的正多边形，其原因可能是由于莫纳克亚山测量的湍流廓线等效层只有6层，而帕拉纳尔测量的湍流廓线等效层具有100层。因此，对于大型光电望远镜，需要尽可能多地获取高分辨率大气湍流廓线数据，以利于包括地面层自适应光学系统在内的各类光电系统性能的评估和预研究。

图9 不同观测台址下激光导引星的位置分布图。(a) 帕拉纳尔下的位置分布；(b) 莫纳克亚山下的位置分布Fig.9 Location distribution of laser guiding stars at different observation stations.(a) Paranal; (b) Mauna Kea

4.3 不同导引星数目下的位置优化分析

本文用遗传算法对3、4颗的导引星也做了位置优化分析，图10(a)、10(b)和图11(a)、11(b)分别是用500条帕拉纳尔和莫纳克亚山的大气湍流廓线数据得到的三颗和四颗导引星的最优位置分布图。从图 10和11中可以看出，不同数目的导引星在同一台址下的位置分布类似，此结果表明在近地面层自适应光学系统中，不同数目的导引星对系统性能的影响远比大气湍流强度对系统的影响要小。

图10 帕拉纳尔下3颗和4颗激光导引星的位置分布。(a) 3颗星的位置分布；(b) 4颗星的位置分布Fig.10 The position distribution of three and four laser guiding stars in Paranal.(a) Three stars; (b) Four stars

图11 莫纳克亚山下3颗和4颗激光导引星的位置分布。(a) 3颗星的位置分布；(b) 4颗星的位置分布Fig.11 The position distribution of three and four laser guiding stars in Mauna Kea.(a) Three stars; (b) Four stars

5 结 论

目前激光导引星常用的正多边形排布模式一直是通过蒙特卡洛法多次模拟不同光学系统得到的，该过程需要消耗大量的计算资源，且模拟过程中用到的大气湍流模型无法反映随时间和空间变化的大气湍流特性。针对这两个问题，本文提出使用遗传算法作为导引星位置排布的方法，简化了地面层自适应光学系统几何模型作为遗传算法的目标函数，并且采用多线程、Numba库和多进程的方法对整个过程加速。此方案作为激光导引星的位置优化方法不仅可以节省大量的时间；而且减少了一些不重要参数引起的计算资源消耗；最重要的是可以根据不同台址的实测大气湍流分析其对导引星位置排布的影响，从而使导引星最大化地提升地面层自适应光学系统的性能。

利用上述方法本文从统计角度，分析了两个实测台址下大气湍流强度对导引星的位置排布影响，以及同一台址下3、4、5颗导引星的位置排布结果。研究结果表明，不同观测台址下导引星的位置排布方式不同，其中获取的方法空间分辨率越高，导引星的位置就越呈规则的正多边形。另外帕拉纳尔观测台址下的导引星位置结果表明，在强湍流集中于地面层的廓线下，导引星位置呈规则的正多边形；在强湍流集中于中高层的廓线下，导引星位置位于视场中心。最后同一台址下3、4、5颗导引星的位置结果表明，导引星的数目对位置排布影响不大，同一台址下不同数目的导引星最优位置分布几乎一致，均呈正多边形或视场中心分布。