变截面梁单元在任意荷载作用下固端内力的统一计算方法

赵志强，丁婷，丁圣果，李绮文

（1.贵阳市建筑设计院有限公司，贵阳550003；2.贵州大学土木工程学院，贵阳550003；3.贵州大学明德学院，贵阳550003）

1 引言

在杆系有限元编程中，总荷载列阵由各单元的固端力列阵集成：

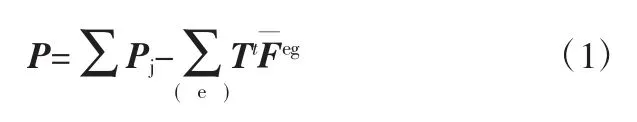
式中，为局部坐标系下的固端力列阵；Tt为坐标转换阵；Pj为结点荷载列阵。

的计算一般均按结构力学固端弯矩表中的计算式，并根据荷载形式用选择转向语句完成计算，对于杆截面变化的单元或较复杂的荷载形式，则存在计算程序的前处理输入冗繁，若采用实体单元，计算结果为应力，需作剖面将应力再转换成该剖面内力。采用基于力法的奇异函数方法及高斯求积法，有效解决了这一难题，编程方便简捷。

2 变截面杆固端内力列阵的统一计算式

2.1 计算固端内力的力法方程

任意变截面杆单元在任意荷载作用下的固端内力计算可用力法导出[1]，仅以连续梁单元为例，单元ij（见图1a）在竖向荷载作用下，计算固端弯矩的基本结构为端部铰支的静定梁，如图1b 所示。

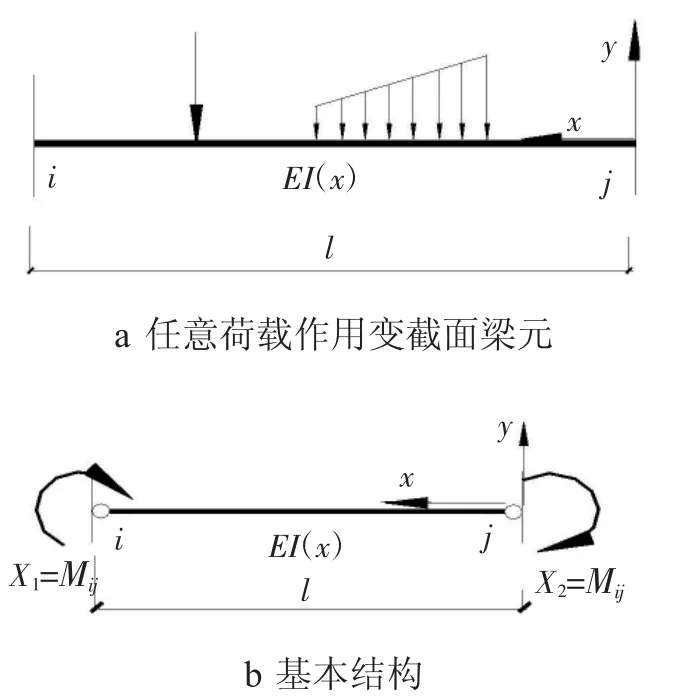
图1 渐变截面杆元及其基本结构

力法典型方程为：

式中，δij为柔度系数；Xi为x方向的力；ΔiP为荷载系数。

方程中的柔度系数δij（i=1，2；j=1，2）计算式为：

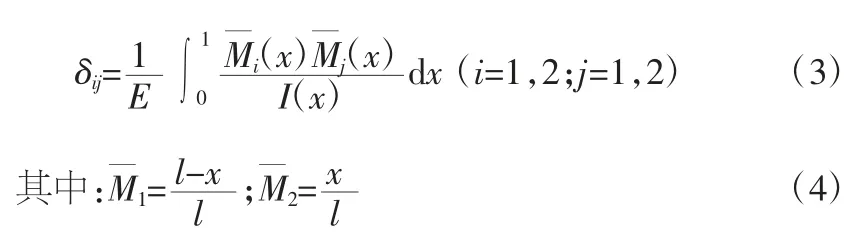
I（x）为杆截面惯性矩：

方程中的自由项：

式（3）和式（6）被积函数是x的分式，很难用一般积分运算完成。可采用高斯求积法进行积分运算。

(1)基坑的周围具有一个边界效应,即在基坑外的湿陷量量会迅速的减小，而基坑内部中心点沉降量最大，其沉降量沿半径方向较为均匀的减小。

2.2 用奇异函数表达的任意荷载作用下基本结构弯矩MP（x）统一公式

基本结构在任意荷载作用下的弯矩MP（x）可采用截面法导出，用奇异函数统一表达为：

该函数在编程中采用条件赋值语句即可实现。

V0为简支梁右端支反力（见图2）；对于每一个集中力Pk（k=1，…，np），几何参数akp为集中力所在位置；对于每一段分布力qk，Δqk（k=1，…，nq），几何参数bskq，bekq分别为分布力的起始位置和终止位置；式（6）已能既括梁上常见的大部分荷载工况（见图2），当作用均布荷载时，取Δqk=0；当作用有梯形分布荷载时，取q0k＞0，Δqk＞0 或q0k＞0，Δqk＜0；三角形分布荷载是梯形分布荷载的特殊情况，取q0k=0，Δqk＞0 或q0k＞0，Δqk=-q0k。

图2 任意荷载作用下的基本结构

2.3 梁变截面高 的表达形式

当梁截面高连续变化时，h（x）是x的连续函数，例如，梯形变截面高的梁（见图3a）

由截面尺寸的几何函数可确定矩形截面梁的截面惯性矩（Ix），如矩形截面

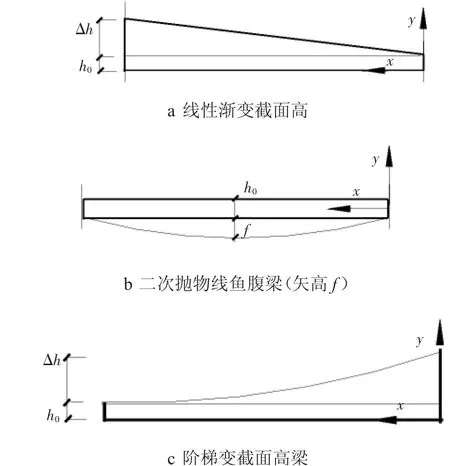
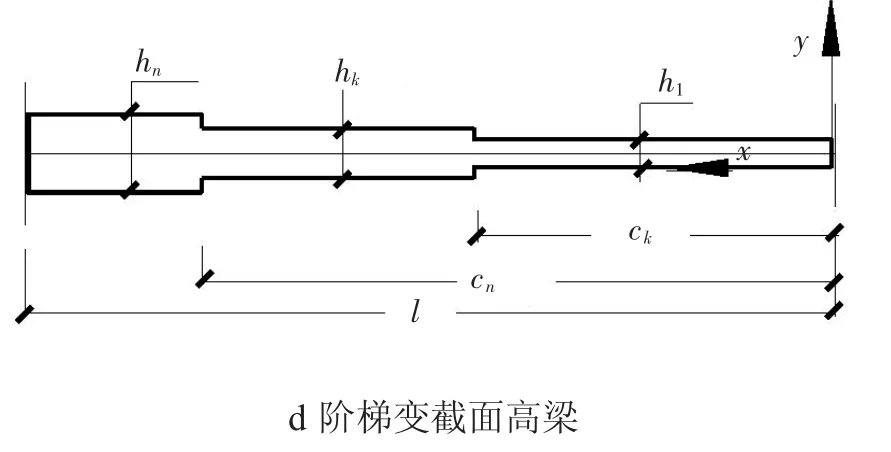
图3 变截面梁

2.4 计算固端弯矩的高斯求积法

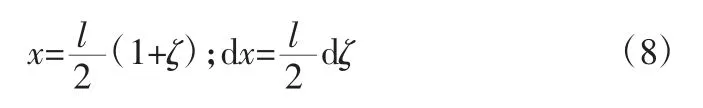
式中，ζi为非等距积分点值，是勒让德多项式方程的根，Hi为权值，nζ为积分点数，其值如表1 所示。

表1 高斯积分点及权值

原则上积分域范围[-1，1]的积分点数nζ可取2，3，…，式（3）和式（6）的积分采用高斯求积法完成而不至造成较大误差的条件是被积函数F（ζ）不存在间断点，经大量算例计算结果分析对比，对积分点数nζ的取值可按如下原则确定：

1）当MP（x）在（0≤x≤1）为连续函数且梁截面高h（x）也连续时，如分布荷载作用下的渐变截面梁，取nζ=3 已能很好地满足计算结果的精度要求；

2）当MP（x）的一阶导数不连续时，如集中力作用的MP（x）图，插值点数宜选多些，在后面算例中均取nζ=7；

3）当MP（x）存在第一类间断点，如梁结间作用有集中力矩时的MP（x）或梁截面分段突变，h（x）存在第一类间断点时，宜将集中力作用点及截面尺寸突变点设为单元结点。

用式（9）完成式（3）和式（6）的定积分运算后，杆的固端弯矩（方程（2）的解）为：

式中，V0ij，V0ji分别为简支梁左、右端剪力。

3 算例

表2 中各算例给出的计算结果精度在大量计算中具有典型性，表明采用本文方法计算的固端内力误差小于1%。

4 结论及讨论

1）采用基于力法的高斯求积运算计算杆单元的固端内力，计算结果精度可达99%以上。

2）方法适用于任意结间荷载作用下的梁单元固端内力计算，编程无须逐一根据荷载形式按结构力学固端内力公式计算。事实上，任何结构力学书籍中也不可能将各种荷载分布形式的固端内力计算概括完全。

3）方法适用于任意渐变截面梁单元，这是在现有杆系有限元程序中是难于实现的，当梁截面变化时，常规有限元程序只能用把梁域细分为较多高阶实体单元，其计算结果以细小单元应力形式给出，对杆系结构的工程应用中，需截面内力的计算结果并不方便。

4）在形成有限元法荷载列阵的编程中，采用本文的计算模型及方法，编程方便，计算力法方程中的柔度系数δij及自由项ΔiP仅需单层几次循环，循环数次根据高斯插值点数决定。

5）本文的方法也宜用于渐变截面单元的局部坐标系单刚推导[4]。因此，完成渐变截面杆系结构在任意荷载作用下的有限元编程完全可行，在这方面做的大量工作表明计算结果精确。

6）当梁域结间存在集中力矩或梁截面分段突变时，由于被积函数存在第一类间断点，将整段梁作为一个单元计算时高斯积分法可能造成较大误差，这种情况可在集力力矩作用点及截面尺寸突变点划分单元结点。

表2 固端内力计算值