多分量权值的树结构立体匹配算法

李亚旋，谢红薇，王春丹，张兴忠

(太原理工大学 软件学院，山西 太原 030024)

0 引 言

立体匹配算法[1,2]可以分为局部立体匹配算法和全局立体匹配算法。通常局部立体匹配算法包括自适应窗口[3]、自适应权重[4]等。然而，在弱纹理区域中局部立体匹配算法的匹配精度未达到理想效果[5]。相对于局部立体匹配算法，全局立体匹配算法[6]通过建立能量函数并最小化该函数来达到全局最优视差值以获得最终视差图。该算法虽然匹配精度有很大提升，但其计算复杂度高导致较慢的运行速度[7]。Yang等[8]提出了非局部代价聚合的方法。不同于之前依靠像素支持区域的方法，其在视差精度和运行速度方面都有了很大了提升。但是由于其权值的计算只考虑了像素点的颜色信息，则计算出相等的边权重会导致非唯一的树结构。Wang等[9]又提出了一种基于置信系数的非局部立体匹配算法，该算法改善了重复纹理区域的匹配精度。

上述的立体匹配算法都得到了较好的立体匹配效果，但还需要进一步提高深度不连续区域的匹配精度。对此，本文提出多分量权值的最小生成树匹配算法，解决了代价聚合阶段相似颜色处的像素点错误连接问题，更准确计算边权值的大小。该方法降低了时间复杂度，并且在深度不连续区域可以得到更为准确的视差图。最后，实验结果验证了算法的有效性和可行性。

1 立体匹配算法实现

本文算法主要融合像素截断强度差和图像梯度计算匹配代价，利用改进的颜色内相关性和颜色信息构建最小生成树，采用Winner-take-all策略计算初始视差值并且使用非局部视差精化来获取最终稠密视差图。本文算法框架如图1所示。

图1 算法框架

1.1 匹配代价计算

匹配代价计算是计算左图和右图的视差值，即将左图作为参考图像，计算参考图在视差范围内与右图的匹配值。建立匹配代价函数是整个匹配算法的基石，其结果最终将影响视差图的匹配效果。匹配代价函数的计算采用的是像素截断的绝对强度差(truncated absolute intensity diffe-rence，TAD)与图像梯度(gradient)相结合的代价方法，其公式如下所示

C(p,d)=α·CTAD(p,d)+β·CGRAD(p,d)

(1)

式中：α和β分别为CTAD(p,d) 和CGRAD(p,d) 的合成权重，用于平衡两种方法所占的比重。CTAD(p,d) 和CGRAD(p,d) 公式分别如下所示

(2)

(3)

上述代价函数既考虑了图像的颜色影响，又结合了图像的梯度大小，可以获得更为准确的匹配代价值。多特征融合计算匹配代价，很大程度上改善图像弱纹理区域或深度不连续区域的匹配性能。

1.2 匹配代价聚合

考虑到各个像素点之间的匹配很容易因噪声而受到影响，导致所求的匹配代价的最低值并不是所期望值，无法计算视差的最优值，所以通过匹配代价聚合，使得聚合后的代价值能够正确反应像素之间的相关性，从而降低噪声对匹配的影响。

1.2.1 多分量权值构建最小生成树

传统的非局部立体匹配算法是通过构建最小生成树(minimum spanning tree，MST)进行代价聚合，从而得到图像中每个像素点对待匹配像素点的作用，考虑到近点和远点的影响，例如，对于距离待匹配像素点远的像素点，该点的权重值很小，这使得可以更准确计算待匹配像素点的代价聚合值。但是该方法在构建最小生成树的过程中，边的权值定义为图像中两个像素点的灰度值之差的3通道最大值，如下面公式所示

(4)

传统方法可能导致相似颜色处的像素点错误连接，且忽略了其它两个通道的边缘重量对最终边缘重量的影响。在此基础上提出一种计算最小生成树边权重的方法，如式(5)所示

(5)

该方法考虑了三通道的像素信息，使得边缘权重函数的鲁棒性增强。再结合改进的颜色内相关性，共同计算边权值信息，使得获得的色彩信息可以更准确获取内部颜色特性，可以弥补原始边权值的颜色分量作为单一分量的不稳定性这一问题，从而减少误匹配的概率。

原始计算像素点的颜色内相关性Iln=[IRtG,IGtB,IBtR]仅仅取决于3个通道的差值，其公式为

IRtG=IR(x,y)-IG(x,y)

(6)

IGtB=IG(x,y)-IB(x,y)

(7)

IBtR=IB(x,y)-IR(x,y)

(8)

因此本文在原始颜色内相关性的基础上进行改进，改进的颜色内相关性记为I′ln=[I′RtG,I′GtB,I′BtR]， 主要计算过程如下

I′RtG=|IR(x,y)-IG(x,y)|2

(9)

I′GtB=|IG(x,y)-IB(x,y)|2

(10)

I′BtR=|IB(x,y)-IR(x,y)|2

(11)

(12)

改进的颜色内相关性将像素点的色彩信息更加具体展现出来，考虑了像素点颜色通道的取值情况，更充分权衡了边权值的大小。由此，将改进的颜色内相关性和颜色信息共同决定边权值的多分量权值信息如式(13)所示

(13)

式中：θ为预定义调整的参数，主要是权衡颜色内相关性和颜色信息在边权值的计算中所起的作用。在获取到边权值的大小后，利用克鲁斯卡尔算法将权值较大的边进行逐一去除，进行最小生成树的构建，为代价聚合提供有力条件。

1.2.2 基于树形滤波算法的代价聚合

基于最小生成树结构，将代价值沿着树结构进行两次遍历，从而完成代价聚合。其具体过程如下：

(1)将叶节点的原始代价自下而上的聚合到MST的根节点，其公式表示如下

(14)

S(p,q) 是用来表示两个像素点之间的相似度，其计算公式如下

(15)

式中：D(p,q)=D(q,p) 表示MST中p和q之间的距离，即边的权值。σ主要用来调整两个节点之间的相似性。

(2)将根节点的原始代价自上而下的聚合到MST的叶节点，其公式表示如下

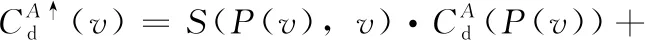
(16)

1.3 视差计算及其精化

视差计算采用WTA策略，公式如下所示

(17)

将计算出的每个像素点的最小代价聚合值选取出来，作为该像素的视差值，从而得到整幅图像的初始视差图。其中，D表示可能的视差范围，并且视差图具有与左参考图相同的大小，并存储每个像素的视差值，如果在已知双目摄像机的情况下，视差图可以通过计算转化为深度图，获取每个像素在空间中位置信息。

视差精化是将上述所得到的初始视差图更进一步优化为高质量的稠密视差图。采用非局部视差精化法作为优化初始视差图的方式。具体过程是依次以左图像和右图像作为参考图像来运行非局部成本聚合方法，以获得两个对应的视差图，利用等式(18)将所有像素划分为稳定或不稳定的像素

dL(x,y)=dR[x-max(dL,0),y]

(18)

式中：dL和dR为左右初始视差图。满足该式的视为稳定点，否则为异常点。使用左右一致性检测(left-right consistency check，LRC)的方法重新计算新的匹配代价值。计算公式如下

(19)

式中：D(p) 表示左视差图，并且对于稳定像素，针对每个视差水平d的每个像素p计算新的匹配代价值，对于所有不稳定像素(由于遮挡、缺乏纹理、镜面反射等)，匹配代价值为零。最后采用代价聚合的方法重新聚合新的匹配代价值，进而得到最终高质量视差图。

2 实验结果及性能分析

本次实验是在具有2.40 GHz的CPU和内存为4 GB的笔记本电脑上进行的。运行环境为Microsoft Studio 2010，并导入OpenCV函数库，使用c++语言进行实验，来验证算法的有效性。所提算法是在Middlebury平台上进行并测试，测试数据集包括4幅标准数据集：Tsukuba，Venus，Teddy和Cones，以可靠地评估本文提出的方法和其它近年来的前沿非局部立体匹配方法在准确性方面的性能。算法中使用的参数见表1。根据实验经验，θ的取值范围应该在[0.2，0.5]之间。

表1 本文立体匹配算法所用参数

2.1 本文算法的实验结果

本文算法实验结果如图2所示。

图2 本文算法实验结果

从图2可以看出，本文算法得到的视差图更平滑，类似于与标准视差图，在边缘部分有很好的效果，比如Tsukuba的桌子边缘区域；在丰富的纹理区域，比如Cones的木板区域，有清晰的匹配效果。

2.2 视差图求取及分析

为了更好展现对比的实验效果图，将非遮挡区域错误像素点标白，比较各个算法的白色区域的覆盖范围，结果如图3所示。图中从上到下依次是MST算法、ST-1算法[10]、ST-2算法、CS-MST算法[11]、CS-ST-1算法、CS-ST-2 算法和本文算法分别对4幅标准图Tsukuba、Venus、Teddy和Cones求取的不同视差结果图。MST是首次提出的基于最小生成树的非局部立体匹配算法，ST是在MST的基础上构建分割树并且ST-2在二次迭代时采用了颜色信息和深度信息，CS算法(CS-MST、CS-ST)考虑了多尺度的图像信息，构建了一种代价聚合模型，可以融合多种匹配算法。

图3 误匹配像素点对比

由图3可以看出本文算法在测试图像的深度不连续和弱纹理区域的白色区域明显减少，比如Venus图的平滑度比其它算法都要平滑，并且Teddy熊猫头部的误匹配像素点比ST-1算法少；Tsukuba书架背景的平滑度和连续性比CS-MST和CS-ST算法效果更精确；Cones的边界处更加清晰明显。

2.3 视差结果分析

为了进一步验证本实验的有效性，针对非遮挡区域(n-occ)、所有区域(all)和深度不连续区域(disc)的误匹配率进行了定量分析，并对各个算法的误差数据进行了比较，其中avgErr表示视差图的平均误匹配率。其误匹配率计算的数学公式为

(20)

式中：dC(x,y) 表示计算得到的视差值，dGT(x,y) 表示真实的视差值，δd表示视差阈值，本文取值1.0，大于该阈值则认为误匹配。

表2为不同的算法用上面4组标准测试图像进行评估的结果，实验结果数据如下。

从表2中可以看出，本文算法的平均误匹配率为5.79%，比ST-1、ST-2、CS-MST、CS-ST-1和CS-ST-2算法分别低1.44%、1.04%、1.09%、0.98%和0.97%。比MST算法仅高0.31%，但是本文算法在Teddy标准图的n-occ、all和disc区域比MST算法分别降低了0.28、0.34、0.05百分点。在Venus上，本文算法比CS-MST、CS-ST-1和CS-ST-2算法在深度不连续区域分别降低了3.75、4.68、3.81个百分点。

针对标准数据集的非遮挡区域匹配率，本文又与近年来几种改进的非局部立体匹配算法(IST-2算法[12]、文献[9]、IMST算法[13])进行了比较分析，结果见表3。

可以看出，本文算法在非遮挡区域的误匹配率比IST-2算法、文献[9]所提算法分别低0.24、0.01个百分比，虽然比文献[9]的结果较高，但在Teddy图的非遮挡区域本文方法效果较好。由此可见本文算法匹配准确度高，改善了深度不连续区域和弱纹理区域匹配率不高的情况，具有较好的鲁棒性，可获得高质量视差图。

2.4 时间复杂度分析

在代价聚合阶段，本文利用改进的颜色内相关性和颜色信息分量作为边权值信息，充分利用的像素色彩之间的信息，相较于MST算法仅单一的选取像素颜色3通道之间的最大值作为边权重，运行速度慢一点；而ST-2算法在进行第2次迭代时融合了颜色和深度信息，以及CS算法要考虑图像间多尺度的交互信息，所以通过比较分析，本文算法比ST-2、CS算法运行速度快，时间复杂度更低，其结果见表4。

表2 不同视差图在不同算法下的误差数据

表2(续)

表3 非遮挡区域中不同视差图在不同算法下的误差数据

表4 运行时间对比/s

3 结束语

本文提出一种改进的多分量权值的非局部立体匹配算法，首先通过像素的截断绝对差和图像梯度融合方法来计算匹配代价值。然后利用克鲁斯卡尔算法将改进的颜色内相关性和颜色信息相结合作为最小生成树的边权值，充分计算了像素之间的色彩信息，不会导致像素出现相同色彩的情况。之后运用树型滤波算法进行代价聚合，最后采用WTA和非局部后处理方法生成精细视差图。

本文降低了图像匹配噪声，在深度不连续区域和弱纹理区域都得到了较好的视差效果，提高了视差图的匹配准确度，由此本文算法具有一定应用价值。由于本文主要利用像素的颜色内相关性和颜色信息作为边的权值，下一步还可以考虑相似颜色的边界范围，提高像素边界的清晰性，使得匹配效果更准确。