超宽视场离轴光学系统畸变一致性校正技术

（北京空间机电研究所，北京 100094）

引言

近年来，随着光学遥感技术的快速发展，为满足海岸带超宽视场和高分辨率的动态监测需求，超宽视场离轴光学系统已成为空间光学遥感器的重要发展趋势[1]。离轴光学系统具有更多设计自由度，可消除轴外像差，具有更加优异的性能，能实现更大视场范围内各性能达到指标，满足相机大幅宽的要求。

本文介绍的某海岸带成像仪相机采用两台超宽视场离轴光学系统，单台光学系统视场角为32◦×1.3°，相机存在弧形畸变且畸变较大。光学设计最大相对畸变＜4%，相机畸变和线阵平行性不一致，都将直接导致最终两台相机图像的拼接质量，因此开展畸变一致性装调校正十分必要。

目前国内外现有的计算机辅助光学系统装调技术都是通过光学零件装调，使得RMS 波像差最小[2]，而并不以畸变作为评价指标，传统装调方法在镜头装调阶段难以开展有效的畸变均衡校正。

1 畸变一致性校正技术

1.1 全链路畸变仿真计算

在计算机辅助装调的方式中，其中常用的一种方式为“反向优化法”[2-3]，对系统进行失调仿真，将设计好的理论系统人为加入失调，建立起系统失调状态的模型库，得到各镜偏转方向与像质、视轴、畸变的多变量全链路仿真计算[4]，从而指导离轴光学系统镜头阶段像质和畸变的均衡校正调整。

将主镜、次镜和三镜各项最大公差输入到CODEV 光学设计软件中，选取初级像差作为校正对象进行仿真，计算离轴三反光学系统在不同偏心、倾斜量值下出瞳面的像差和相对畸变[5-7]。图1列出了各反射镜（主镜、次镜和三镜）和失调量对三阶像差的影响，如彗差、像散和畸变值的变化。

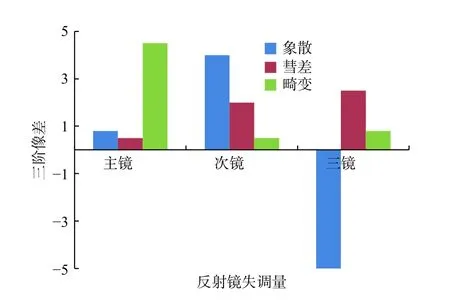
图1 各反射镜失调量对三阶像差和畸变的影响Fig.1 Influence of mirror misalignment on third-order aberration and distortion

由于该系统畸变为弧形，仿真计算分析主镜倾斜和平移对像散、彗差和绝对畸变值的影响，如表1所示。

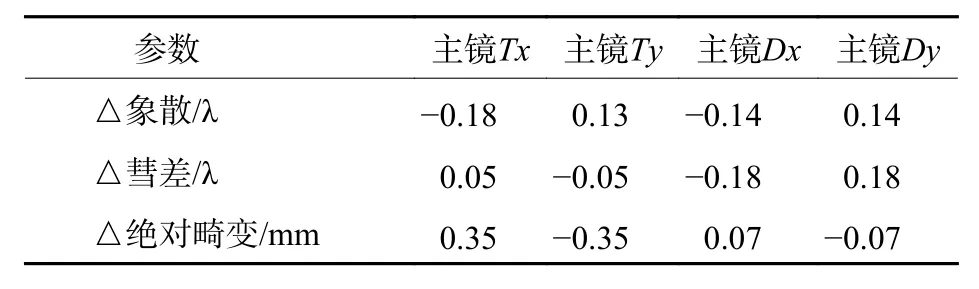
表1 主镜失调量对像差和畸变的影响Table1 Influence of primary mirror misalignment on aberration and distortion

从图1和表1可以看出，主镜对像散影响较小，但对畸变影响较大，而次镜和三镜对像差影响较大。因此，通过次镜和三镜对光学系统波像差进行校正，通过主镜Tx和Ty对光学系统畸变进行校正。

1.2 高精度畸变测量

以往的畸变测量方法如精密测角法[8]等受人文因素影响较大，测量结构不稳定[9]。本文结合工作实践，采用干涉仪、光电自准直仪和激光跟踪相结合的光学系统畸变测量方法[10-11]，并根据实际测量值对镜头畸变进行一致性装调校正。图2给出了利用干涉仪、光电自准直仪、激光跟踪仪和跟踪仪靶球搭建的测量光路。

图2 测量光路示意图Fig.2 Schematic of measuring optical path

该方法利用干涉仪接收到的光波波前power值对球面反射镜位置非常敏感的特性，并结合激光跟踪仪的空间几何量精密测量，可精确测量光学系统轴上和轴外视场的像高，并结合光电自准直仪的精密测角，可实现光学系统焦距的高精度测量。测试步骤如下：

1） 首先利用干涉仪建立光学系统轴上视场和轴外视场的波前测试光路；

2） 跟踪靶球放置在光学系统焦面位置，调整靶球使得干涉条纹成为零条纹，使用跟踪仪记录靶球的空间位置（x1，y1，z1），使用光电自准直仪测量干涉仪平面反射镜的法线角度值（h1，v1）；

3） 将干涉仪偏转一定的角度（约0.2°），记录跟踪仪靶球的空间位置（x2，y2，z2）和干涉仪平面反射镜的法线角度值（h2，v2）；

根据两次记录的跟踪仪靶球的空间位置和干涉仪平面反射镜的法线角度值，按（1）式和（2）式可计算得出被测光学系统的焦距值为

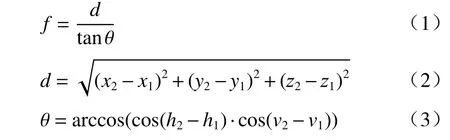
式中：f为被测光学系统焦距；d为跟踪仪靶球的空间位置变化量；θ为干涉仪平面反射镜的法线角度变化量。

4） 绝对畸变[12]在数值上是以理论像高h和主光线与理想像面相交的实际像高H之差表示

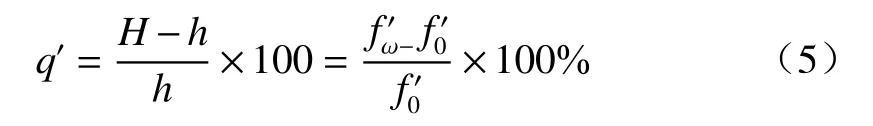
相对畸变值q′表示了光学系统不同视场下焦距值的不同。

2 实际装调

某海岸带离轴光学系统沿线阵方向（X方向）的畸变较大[13]，且垂直线阵方向（Y方向）存在弧形畸变。该相机线阵方向（X方向）最大相对畸变设计值为3.729%，边缘视场在Y方向的畸变约为1.9 mm，如图3所示。

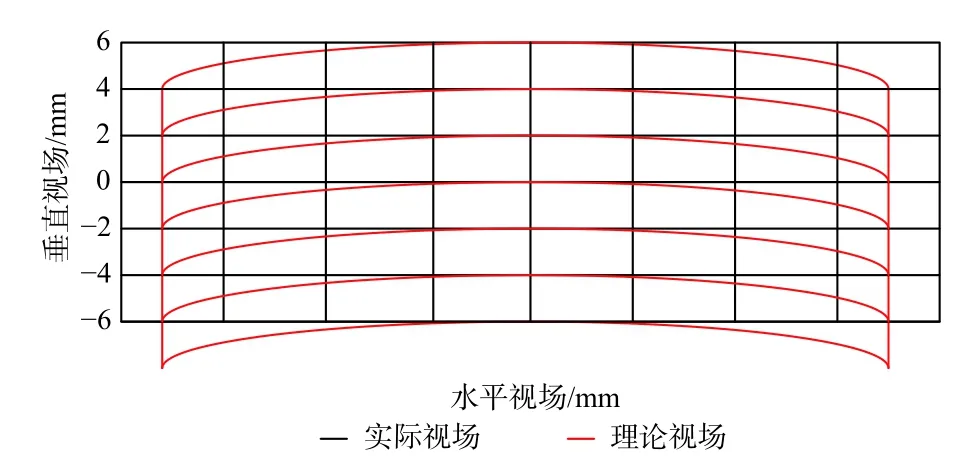
图3 光学系统畸变图Fig.3 Distortion grid of optical system

该相机CCD 光敏区宽度为2.2 mm，CCD 器件在成像区域中的位置如图3所示，要求（0°，0°）中心视场在焦面上的像点与焦面B4 谱段下边缘距离0.5 mm，（16°，1.3°）和（−16°，1.3°）边缘视场在焦面上的像点与焦面B1 谱段上边缘距离0.6 mm，如图4所示。

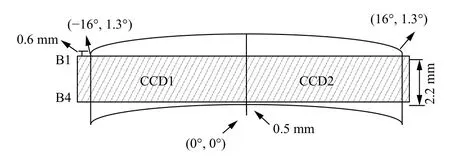
图4 CCD 器件在成像区域中的位置Fig.4 Position of CCD device in imaging region

为了使得CCD 焦面放置在整个成像区域的中心位置，同时还要求两台相机的焦面线阵平行性优于1'，这就要求镜头在系统精密装调阶段对弧形畸变进行一致性校正调整。

首先，根据自准干涉测量得到超宽视场离轴光学系统轴上和轴外各视场的波像差，使用计算机辅助装调求解出光学系统失调量，求得三镜和次镜自由度的变量值和方位进行像质精密调整，测试光路如图5所示。

图5 装调测试现场Fig.5 Adjustment and test site

其次，根据高精度畸变测试系统进行畸变测量，干涉仪的偏转角度和跟踪仪靶球的空间位置变化量按（1）式得到光学镜头边缘视场的焦距，从而获得镜头绝对畸变曲线。通过自编软件解算主镜的倾斜量作为自变量进行优化计算，使得弧形视场两边视场的绝对畸变差值最小。通过对镜头畸变进行2次迭代调整和测试，最终镜头畸变校正前后的曲线测试如图6所示。

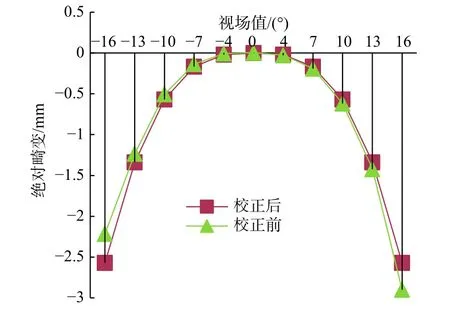
图6 绝对畸变校正前后曲线对比Fig.6 Comparison of curves before and after absolute distortion correction

最后，再通过三镜的倾斜量对镜头像质进行补偿调整[14-15]。最终，波长为632.8 nm的各个视场波像差平均值满足了光学系统成像质量的要求。

工程中对两台超宽视场离轴光学系统进行了实际畸变装调校正，两台相机最终的最大相对畸变和波像差值如表2所示。

表2 两台相机测试结果Table2 Test results of two cameras

两台相机最后相对畸变控制一致性精度优于0.1%，全视场平均波像差都满足指标要求。

3 结论

本文开展了兼顾像质和畸变的多变量全链路仿真，建立了高精密畸变测量系统，实现了超宽离轴光学系统畸变补偿的交互迭代调整。实验结果表明，该方法测量精度高，具有较高的重复性和实用性。