基于微面元理论的“猫眼”目标回波散射偏振特性研究

（北京信息科技大学 仪器科学与光电工程学院，北京 100192）

引言

激光探测技术中光电系统自身的“猫眼”效应得到了广泛的应用。“猫眼”效应的定义主要包含两点内容：1） 照射到目标光学窗口的激光，经过位于其焦平面上具有高反射率的探测器的反射，反射光方向将会沿激光入射方向原路返回；2） 反射光的强度远远高于背景中其他目标的回波强度。该定义主要描述了光电系统回波方向和强度2个特征[1]，通常将符合该定义的目标称为“猫眼”目标。

基于“猫眼”效应的激光探测技术，是对目标进行探测和实施精准打击的有效方式之一[2]。激光主动探测技术主要采用强激光照射的方式以达到对探测器干扰损伤的目的[3]，可通过分析被探测目标回波信号偏振度的变化判断其探测器表面的损伤程度[4]。因此，研究“猫眼”目标回波散射的偏振特性具有十分重要的意义。

偏振是光的基本特性之一，光与不同的介质或者同一介质的不同状态相互作用时，其偏振态都会发生改变[5]。偏振态的改变一方面取决于介质的材料及其表面粗糙度等物理特性，另一方面取决于入射角、观测角等探测方式的不同。利用偏振探测技术不仅可以获得被测目标表面的回波强度信息，而且能够得到传统探测技术无法获取的目标表面偏振特性，如偏振度、偏振角等。偏振信息可以反映目标的形貌以及纹理特征，大大提高了目标探测识别精度。依据这一特点，偏振探测技术在目标探测与识别、偏振遥感等方面得到了广泛的应用[6]。

双向反射分布函数（bidirectional reflectance distribution function，BRDF）反映了反射介质的本质属性，描述光波在目标表面反射后的能量分布情况[7]。偏振双向反射分布函数（polarized bidirectional reflectance distribution function，pBRDF）是在BRDF

基础上发展起来的，是表征粗糙表面反射偏振特性的典型模型，描述了光波入射到目标表面后，反射光在上半球空间的分布情况及偏振特性，表征了目标表面散射偏振特性与入射角、探测角、复折射率、表面粗糙度等参数之间的数学关系，是获取目标表面散射偏振信息的有力手段。偏振度的计算方式主要有实验测量和理论建模。实验测量是通过实验分析得出偏振度与各参数之间的对应变化关系，常用方法是斯托克斯矢量法。理论建模是通过理论推导得出偏振度与各参数之间的数学表达式，从而得到特定条件下偏振度的大小[8]。实验测量的方式受到实验条件与实验方法的限制，难以得到任意条件下的偏振度，因此利用部分偏振度测量值验证相应的理论模型是必要的。国内外有关学者主要是对现有的模型进行改进，推导出了适用于不同情形的模型[9]。

本文根据偏振双向反射分布函数模型，结合“猫眼”目标探测的特点，基于微面元理论，推导了“猫眼”目标在线偏振光探测条件下的回波散射偏振度表达式。利用Matlab 仿真得到“猫眼”目标回波偏振度与目标表面粗糙度参数σ的关系曲线。设计实验方案并搭建实验测量系统，选择经过不同砂纸打磨的硅片作为“猫眼”目标进行实验，得到“猫眼”目标回波散射的偏振度随其表面粗糙度的增大而减小的结论。实验结果表明，“猫眼”目标回波散射的偏振度变化趋势与Matlab 仿真结果一致。

1 偏振双向反射分布函数模型

1.1 双向反射分布函数（BRDF）

为了表征物体表面反射光的空间分布与传输特性，1977年Nicodemus 提出了双向反射分布函数（BRDF）的概念[10]。BRDF的定义为经过目标表面反射沿着 (θr,φr)方向出射光波的辐亮度dLr(θi,θr,∆φ)与沿着 (θi,φi)方向入射到目标表面光波的辐照度dEi(θi,φi)之比，即：

式中：θ、φ分别表示入射、反射光线的天顶角和方位角；下标i、r分别表示光波的入射和反射；∆φ=φi−φr为入射面和反射面的相对方位角，λ为入射光的波长。图1给出了BRD 定义的几何角度关系，目标表面法向为z。

图1 BRDF 几何关系图Fig.1 Geometric relation schematic of BRDF

通过测量入射光波辐照度及经过物体表面反射光波的辐亮度计算BRDF的方法并不常用，常常通过理论推导建立物体表面反射光传输特性的函数模型及其数学表达式。物体的表面大多数比较粗糙，其表面的反射也并非简单的镜面反射，因此相应的BRDF函数模型也比较复杂。常用的BRDF模型有:Torrance-Sparrow（T-S）和Beard-Maxwell（B-M）模型。T-S模型是根据镜面反射微面元理论得到的，其概率分布函数为高斯分布。物体表面粗糙度参数大于或等于入射光波长，就可看作是由微面元构成[11]。本文的理论推导将基于T-S BRDF模型，图2为微面元模型的角度关系。

图2 法向 zµ的微面元与法向 z的目标表面相对位置关系Fig.2 Positional relationship between zµ-normal microfacet and z-normal object surface

基于微面元理论的T-S BRDF表达式为

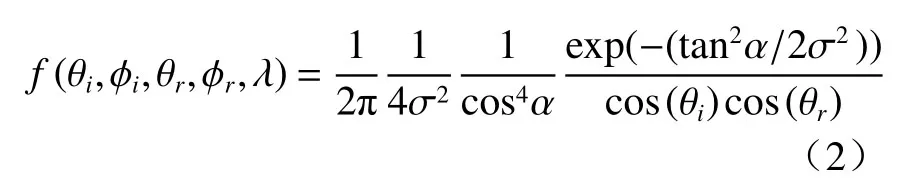
式中：σ为目标表面的粗糙度参数，其值越小（大）表示目标表面越光滑（粗糙）；α为微面元法线zµ与目标表面法线z的夹角；β为光波入射方向与微面元法线zµ的夹角。则有：

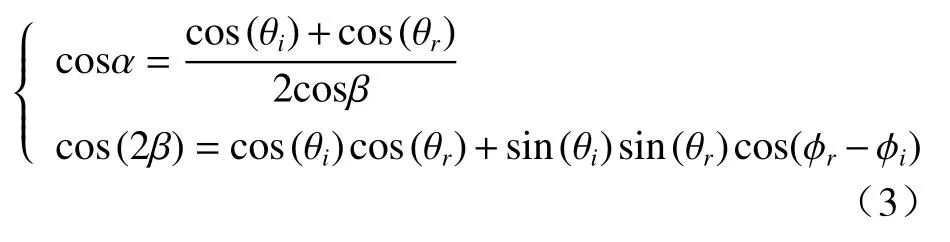
1.2 偏振双向分布函数（pBRDF）

pBRDF是在BRDF模型基础上考虑偏振特性推导而来的，由电磁场理论可知，散射光与入射光之间可通过琼斯矩阵建立联系，即：

式中：上标i、r分别表示入射和散射分量；下标S、P分别表示电场分量垂直和平行于探测面；η表示光线与微面元和目标表面入射面或反射面之间的夹角[12]。那么，琼斯矩阵可以表示为

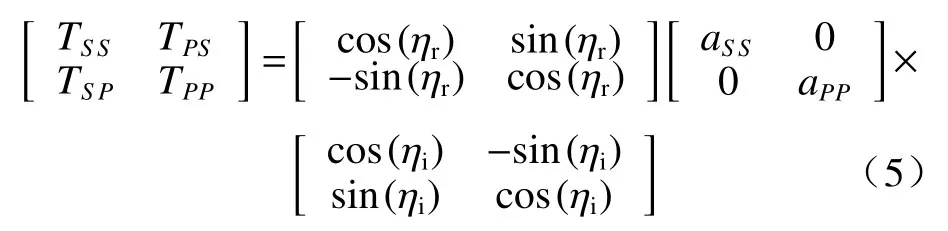
其中，

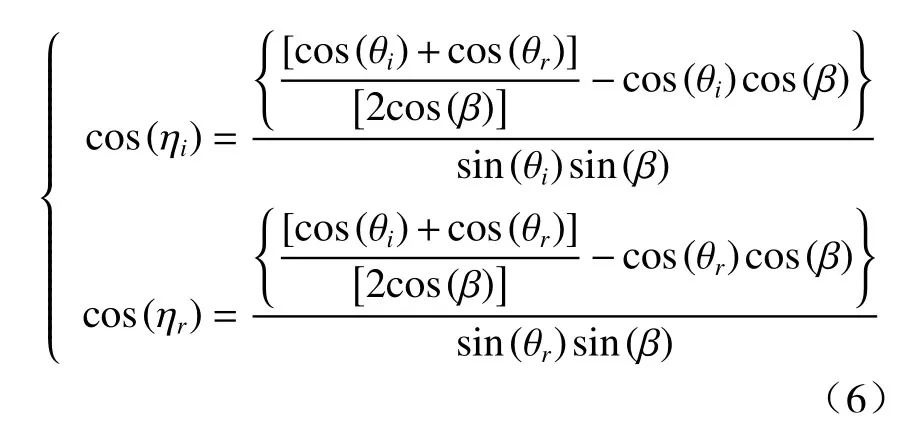
式中：aSS、aPP为菲涅尔振幅反射系数，可表示为

其中，

复折射率nt=n−ix，n、x分别表示材料复折射率的实部与虚部，x由光波在介质中传播的衰减决定。由（4）式和（5）式可得琼斯矩阵各项的表达式为

由于穆勒矩阵与琼斯矩阵之间存在转换关系，通常采用穆勒矩阵来描述光波偏振态的传输过程[13]。

从琼斯矩阵可得到穆勒矩阵各元素的表达式：

式中上标“*”表示复共轭。根据穆勒矩阵元素和（2）式，可以将标量微面元模型的BRDF 进行推广得到pBRDF的矩阵形式[14]，即：

式中：j、k的取值范围是0～3。

半球定向反射（HDR）是指BRDF 在目标表面上半球空间进行积分，其表达式为

由图3可知，平行光正入射到透镜表面并聚焦到其焦平面上，位于透镜焦平面上的目标可以看作由一系列微面元构成，入射到微面元的光波向其上半球空间反射，部分光波在微面元上反射后被透镜接收并按照原光路返回。τ为被透镜接收的反射光投射在微面元法平面的最大夹角。对原路返回的光波进行积分运算，可得：

图3 HDR 示意图Fig.3 HDR schematic

根据穆勒矩阵及T-S pBRDF模型，可以得到入射光和反射光的斯托克斯矢量的传递关系，由入射光的斯托克斯矢量Si得到反射光的斯托克斯矢量Sr[15]为

2 “猫眼”目标回波散射偏振特性模型的建立

2.1 自然光散射偏振特性模型

偏振度定义为完全偏振光的强度与该光波的总强度之比[16]，即

自然光的斯托克斯矢量为

自然光的散射光斯托克斯矢量为

因此得到自然光散射的偏振度表达式为

2.2 线偏振光散射偏振特性模型

入射线偏振光的斯托克斯矢量为

线偏振光的散射光斯托克斯矢量为

因此得到线偏振光散射的偏振度表达式为

由（16）式～（20）式可知，“猫眼”目标表面回波偏振度与入射角θi、探测角θr、复折射率nt、目标表面粗糙度参数σ有关。在激光正入射到“猫眼”目标的情况下，θi=0，nt=3.826+0.015i，将目标表面粗糙度参数σ代入到推导的“猫眼”目标表面回波偏振度表达式中，利用Matlab 仿真得到“猫眼”目标回波散射偏振度与目标表面粗糙度参数σ的关系曲线，如图4所示。由图4可知，随着目标表面粗糙度参数σ的增大，“猫眼”目标表面回波散射偏振度逐渐减小。

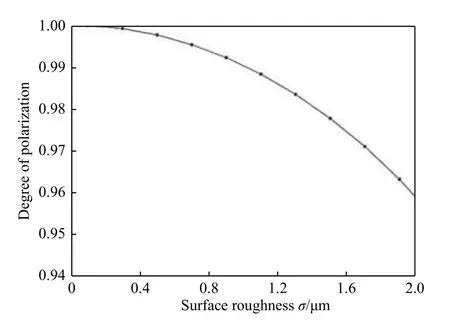
图4 “猫眼”目标回波散射偏振度与目标表面粗糙度的关系曲线Fig.4 Relationship between DOP and σof cat's eye target

3 实验与分析

实验测量系统原理如图5所示。该系统主要包含光源、扩束准直镜、半透半反镜、透镜、“猫眼”目标、精密三维移动平台、偏振片、光功率计。其中，光源采用CNI公司型号为MRL-III-671的固体激光器，该激光器的波长为671 nm，最大输出功率为200 mW，功率稳定性小于1.5%，光束发散角小于1.5 mrad。测得其出射激光的偏振度接近100%，可视为线偏振光。光功率计选择Thorlabs公司的PM100D系列功率计，PM100D可以连接近30种光电、热电、焦电探头。测量波长范围从0.19 μm～25μm，功率范围从皮瓦到几百瓦。

图5 测量原理示意图Fig.5 Schematic diagram of measuring principle

激光器发出的线偏振光经过扩束准直镜和半透半反镜后入射到透镜1表面，透镜1将光波聚焦在其焦平面上。调节精密三维移动平台使“猫眼”目标位于透镜1的焦平面，不断改变激光焦点在目标表面的位置，用光功率计测量并记录目标表面不同位置的回波功率，通过理论计算得到目标表面回波的偏振度。实际测量光路如图6所示。

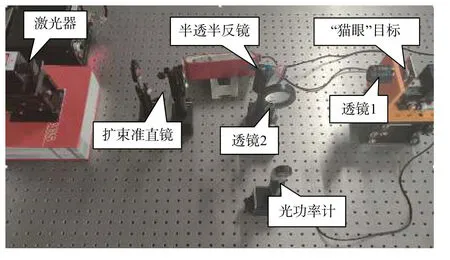
图6 “猫眼”目标回波偏振度测量装置Fig.6 Measuring device of degree of polarization for cat's eye target echo

在光电探测领域，光电系统因其自身的“猫眼”效应往往容易被探测并受到强激光的干扰。原本光滑的探测器表面会受到不同程度的损伤，从而使其表面粗糙度发生变化，探测器表面粗糙度的变化会造成回波偏振特性发生改变。为了验证“猫眼”目标表面粗糙度与回波偏振度之间的关系，实验中选择表面粗糙程度不同的硅片作为“猫眼”目标，进行目标表面回波散射偏振特性分析。硅片表面形貌由Zygo Lamda公司的ZeGageTMPRO HR 光学表面轮廓仪进行检测，该仪器采用非接触式测量技术，不会造成待测目标表面任何损伤，表面定量计量精度可达到纳米级。图7（a）～7（e）为光学表面轮廓仪拍摄的硅片表面的形貌图，硅片表面粗糙度参数测量值见表1所示。面粗糙度参数Sq为面均方根高度，其数值越大（小），表示目标表面越粗糙（光滑）。

图7 硅片表面轮廓测量结果图Fig.7 Measurement results of silicon wafers surface profile

表1 粗糙度参数测量结果Table1 Measurement results of roughness parameters

由微面元理论可知，目标表面粗糙度是影响目标表面反射光偏振特性的重要因素[17]。本文主要研究“猫眼”目标回波散射的偏振度与其表面粗糙度之间的关系。保持其他实验条件不变，分别取硅片的面均方根高度Sq为0.067 μm、0.554 μm、0.726 μm、1.651 μm、1.893 μm，通过理论计算得到硅片表面回波偏振度依次为98.83%、98.16%、96.08%、94.91%、94.6%。绘制硅片回波偏振度与其表面均方根高度Sq的关系曲线，如图8所示。

由图8可知，随着目标表面均方根高度Sq的增大，目标回波散射的偏振度将减小。这是因为当硅片表面粗糙度增大时，目标表面的遮蔽效应也将增强，同时入射光在目标表面发生多次反射的概率增大，导致漫反射增加，反射光的退偏现象越来越严重[18]。结合Matlab 仿真结果与实际测量结果，可以看出“猫眼”目标回波散射的偏振度随目标表面粗糙度的增大而减小。因此，目标表面粗糙度是影响“猫眼”目标回波散射偏振特性的重要因素。

图8 目标回波偏振度与表面均方根高度Sq关系图Fig.8 Relationship between DOP andSq

4 结论

基于微面元理论偏振双向反射分布函数（pBRDF）模型，推导了线偏振光在“猫眼”目标表面回波散射的偏振度表达式，结果表明：“猫眼”目标表面回波散射偏振度与目标表面粗糙度、复折射率等材料物理特性以及入射角、观测角有关。主要研究“猫眼”目标表面粗糙度对其表面回波散射偏振度的影响，利用Matlab 仿真得到“猫眼”目标回波偏振度随目标表面粗糙度参数σ的增大而减小。选择经过不同砂纸打磨的硅片作为“猫眼”目标进行实验，当硅片表面均方根高度分别为0.067 μm、0.554 μm、0.726 μm、1.651 μm、1.893 μm时，其表面回波偏振度的测量值依次为98.83%、98.16%、96.08%、94.91%、94.6%。硅片表面越粗糙，其表面回波的偏振度越小。实验测量结果与仿真结果具有一致性。通过探测“猫眼”目标回波的偏振度判断目标光电探测器表面的损伤程度，在光电探测领域具有十分重要的意义。