银川市红墩子矿区钻孔亚粘土数据kriging插值方法比较研究
孙 涵
(中国地质大学 信息工程学院,北京 100083)
0 引言
地质钻孔数据能够提供鉴别查明矿体、探知矿产资源分布和判定地质地层情况的信息[1],准确表达地质体内的各种地质构造[2],提高地质分析的直观性和准确性[3]。空间插值作为从已知地理空间向未知地理空间探索的主要方法[4],其主要任务是基于采样点的测量值模拟未知点或区域的预测值[5]。利用离散的钻孔数据采用空间插值的方法进行地质内部岩石或矿产的高程预测和可视化,是预估矿区岩石和矿产分布的重要手段。
1 问题提出
红墩子矿区是宁夏自治区近年来勘查发现的大型整装煤田[6],开采量大,作业消耗多,对其的研究大多针对煤矿的特征和开采、施工的建议、人力资源管理和周围生态环境整治等,而几乎没有对该矿区地质构造或矿产分布的高程预测的研究。本文以该矿区中北段较为密集分布的亚粘土数据为例,使用不同克里金插值方法对亚粘土分布的高程进行预测,综合预测误差、插值结果的统计特征和分布图来比较不同方法的插值效果。
1.1 研究意义
通过对亚粘土数据的高程进行插值预测,选取最优的克里金插值方法,一方面为红墩子矿区中北段的矿产开采、矿产分布和地质构造研究提供插值方法参考,获得岩石或矿产较为准确的高程分布面数据,从而在开采煤矿、环境整治等方面一定程度上节省人力物力;另一方面探讨利用钻孔数据对岩石高程分布进行预测时使用克里金方法进行插值的一般思路,进而为其他地区的岩石高程预测提供参考[7]。
1.2 研究区概况
红墩子矿区位于宁夏回族自治区东部,隶属银川市兴庆区管辖[8]。矿区呈南北向条带状展布[9],北起银川市和石嘴山市市界,南至水洞沟,西以黄河为界,东与内蒙古自治区相邻[10],南北长约35km,东西宽约10km,面积约200km2[11]。本次研究数据集中在红墩子矿区的中北段,为了得到较好的插值效果,将研究区缩小,选择红墩子矿区的中北段进行插值,在ArcGIS中对原始矿区进行了裁剪(图1)。
2 数据来源及处理
2.1 数据来源
本文利用的亚粘土高程数据共有47个,全部来源自“全国重要地质钻孔数据库服务平台”,钻孔数据的地质工作类型为矿产地质勘查钻孔。
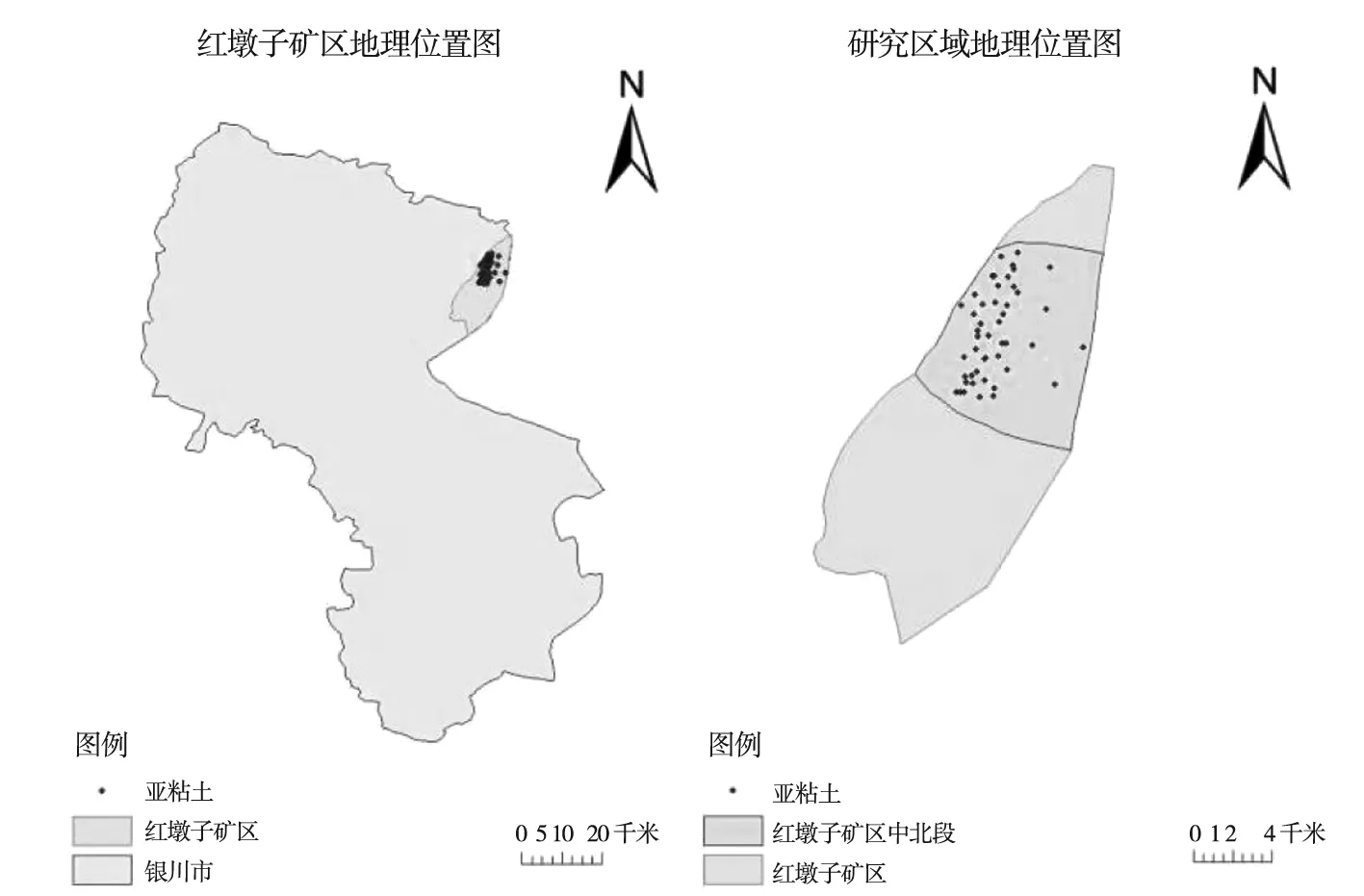
(1)银川红墩子矿区地理位置 (2)插值区域图1 研究区概况
2.2 数据处理
从银川市全部钻孔数据中通过查询检索的方式筛选出红墩子矿区的数据,并根据矿产地质勘查钻孔所包含的钻孔类型进行第二次筛选,从中先选取具有至少十层岩性的100条数据,然后再利用Excel表格的筛选功能进行第三次筛选,获得亚粘土数据共48个,并通过孔口高程和岩层深度计算出亚粘土的高程。将第三次筛选后的数据通过ArcGIS导入成为点数据。
2.3 数据探索与分析
2.3.1 正态分布
克里金插值要求数据要服从正态分布,插值效果才能更好,如果不能较好符合正态分布,则需要进行数据转换[12]。对于本次研究数据进行正态分布检验使用了正态QQ图检验。当数据符合正态分布时,正态QQ图拟合直线应该是沿对角线分布。对本次实验数据进行正态QQ图分析,未进行变换时数据基本沿对角线分布,但仍有一定偏差。进行对数变换和幂变换尝试,最终确定使用幂变换且指数为-0.5时符合正态分布最好(图2)。
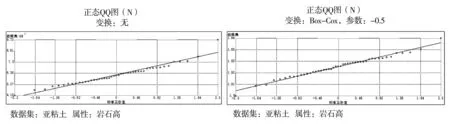
图2 数据正态QQ图
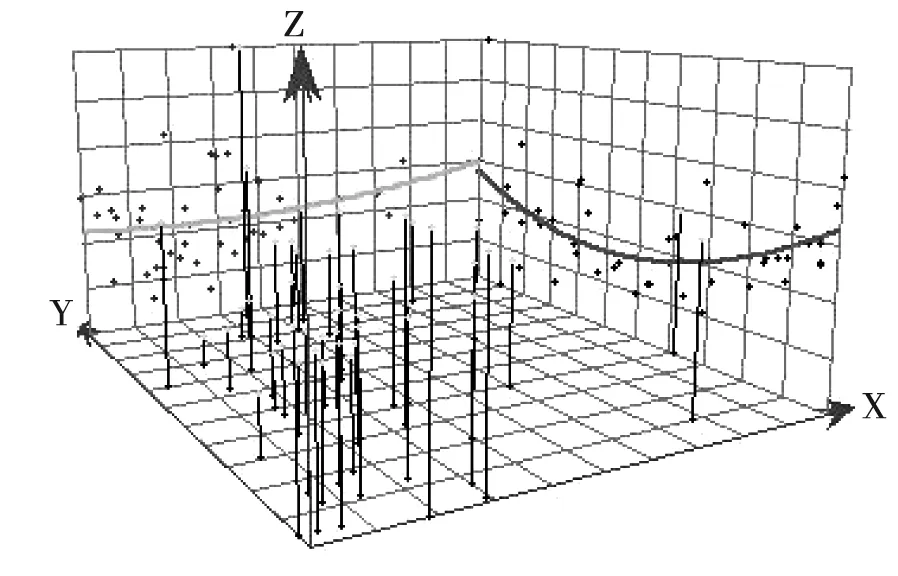
图3 趋势分析三维散点图
2.3.2 趋势分析
趋势分析三维散点图,能够检验数据的全局趋势。在ArcGIS地统计模块中的探索性分析中使用趋势分析功能(图3),X轴代表南北方向,Y轴代表东西方向,Z轴代表亚粘土岩石高程。南-北方向的亚粘土岩石高程分布趋势,可以看出大致为一阶趋势,有轻微二阶趋势。东-西方向上,岩石高程存在较明显的二阶趋势。由此,我们可以做出基本假设,本研究数据存在趋势为一阶或者二阶,但具体是一阶还是二阶拟合效果更好需要后续验证。
3 研究方法
3.1 克里金插值
本次研究采用了四种克里金插值方法,其基本原理和计算方法如下所述。
3.1.1 普通克里金插值法
普通克里金插值法以变异函数理论和结构分析为基础[13],利用原始数据和半方差函数,对区域化变量的未知采样点进行无偏估值的插值方法[14],其公式如下:
(1)
式中:Z(x0)为x0点的估计值;N为样本区钻孔总数;λ为克里金权重系数;Z(xi)为xi点的真实值。
3.1.2 简单克里金插值法
简单克里金插值法也是区域化变量的线性估计,它假设数据变化成正态分布,认为区域化变量Z的期望值为某一常数,其公式如下:
(2)
式中:Z(x0)为x0点的估计值;m为区域化变量Z的期望值;N为样本区钻孔总数;λ为克里金权重系数;Z(xi)为xi点的真实值;m(xi)为xi点的期望值。
3.1.3 泛克里金插值法
泛克里金插值法是普通克里金法的扩展,它将解释变量添加到模型中,以解决与普通克里金方法相关的平稳性问题[15],并考虑了漂移和波动的总和[16]。
3.1.4 协同克里金插值法
协同克里金插值法是一种多变量估值方法[17],采用交叉协方差和交叉半变异函数建模,以得到区域化变量的无偏和最优估计[18],通常用于感兴趣的变量(主变量)抽样较差,而其他变量(次变量)抽样较密集的情况[19],从而可以有效提高插值精度。协同克里金插值法的公式如下:
(3)
式中:Z(x0)为x0点的估计值;Z(xi)为初始变量xi的真实值;Z(xj)为同位二级变量xj的真实值;N和M为初级变量和同位二级变量的个数;αi和βj需要确定的协同克里金加权系数。
3.2 半变异函数模型
不同类型的半变异函数模型会影响未知值的预测,不同种类现象的最准确拟合模型不同。本次研究在ArcGIS地统计模块提供的11种半变异函数模型中选取了最常用的四种进行研究分析,分别为三角函数模型、球面函数模型、指数函数模型以及高斯函数模型。
3.3 交叉验证
本次研究采用了交叉验证的方法对插值结果进行比较,其五个参数分别为:平均误差(Mean Error,ME),均方根误差(Root Mean Square Error,RMSE),标准平均误差(Mean Standardized Error,MSE),标准均方根误差(Root Mean Square Standardized Error,RMSSE),平均标准误差(Average Standard Error,ASE)。其中:平均误差越接近0越好,均方根误差越小越好,标准平均误差越接近0越好,标准均方根误差越接近1越好,平均标准误差越接近均方根误差越好[13]。根据最优规则,对五个参数做了线性相加,作为判断插值结果好坏的辅助工具,在各项参数均很接近的情况下,给出用数字表征的最佳方法。该公式的数值越小,说明预测误差越小,插值效果越好。公式如下:
E(xi)=|ME(xi)|+RMSE(xi)-MIN{RMSE(x1),RMSE(x2)…RMSE(xj)}|+
|MSE(xi)|+|RMSSE(xi)-1|+||RMSE(xi)-ASE(xi)|-
MIN{|RMSE(x1)-ASE(x1)|,|RMSE(x2)-
ASE(x2)…|RMSE(xj)-ASE(xj)||}|
(4)
式中E(xi)为交叉验证判断值,x1到xj为拿来作对比的全部插值的交叉验证值,xi为本次插值的交叉验证结果,0≤i≤j。
4 结果分析
4.1 岩石高程趋势比较
在不考虑各向异性的情况下[7],选取普通克里金函数的高斯模型,只改变阶数,从交叉验证结果来看(表1),虽然二阶平均值较小,但其他四个参数均不如一阶更好。使用交叉验证判断公式,可以发现二阶数值明显大于一阶。因此从交叉验证结果来看,一阶趋势较二阶趋势更好。

表1 趋势分析的交叉验证结果
从插值结果图来看(图4),一阶趋势下结果图高程分布更加均匀,极大值和极小值范围较少,多集中在中等高程范围,一阶趋势插值结果较二阶趋势更好。因此,对于本次研究数据,其更加符合一阶趋势。
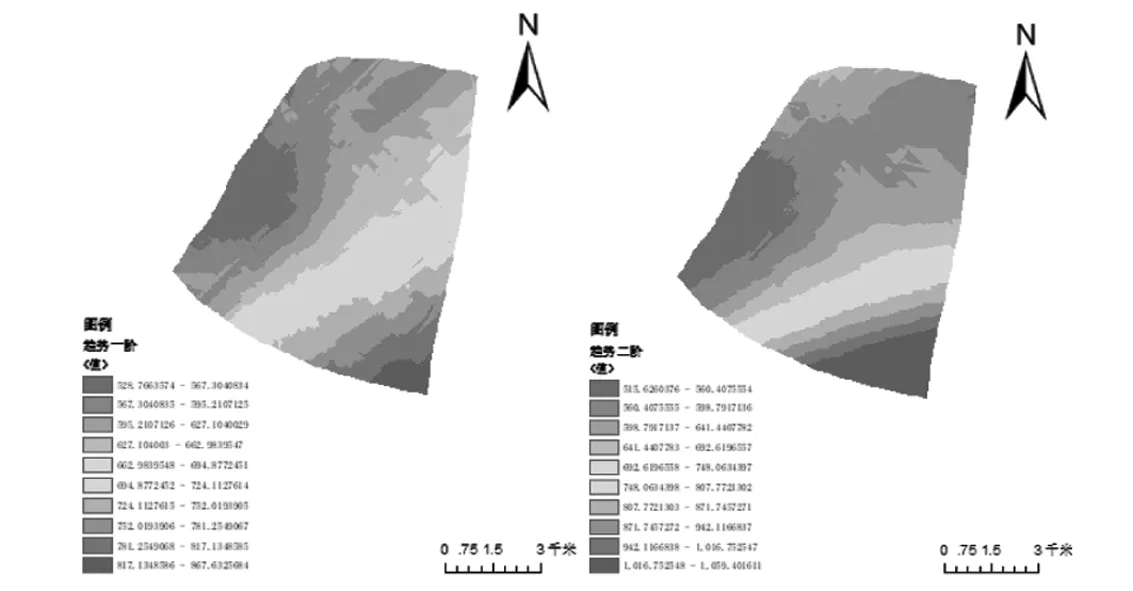
(1)一阶趋势 (2)二阶趋势图4 一阶和二阶趋势插值结果图
4.2 步长数目比较
在确定一阶趋势的条件下,考虑各向异性,对四种克里金插值分别用四种半变异函数模型进行插值。在前面探索性数据分析中,认为普通克里金和泛克里金最优步长数目在12、13左右,简单克里金最优步长数目在20、21左右,协同克里金最优步长数目在7、8左右。
4.2.1 普通克里金插值法
对岩石高程进行普通克里金插值,根据探索性分析确定的步长数目在12、13左右,在研究最优步长数目时步长选择范围为9-14。四种半变异函数模型下的最优步长数目确定运用公式判断方法。从交叉验证结果来看(表2),分别对于三角、球面、指数以及高斯函数模型的最优步长数目为10、11、12和10。
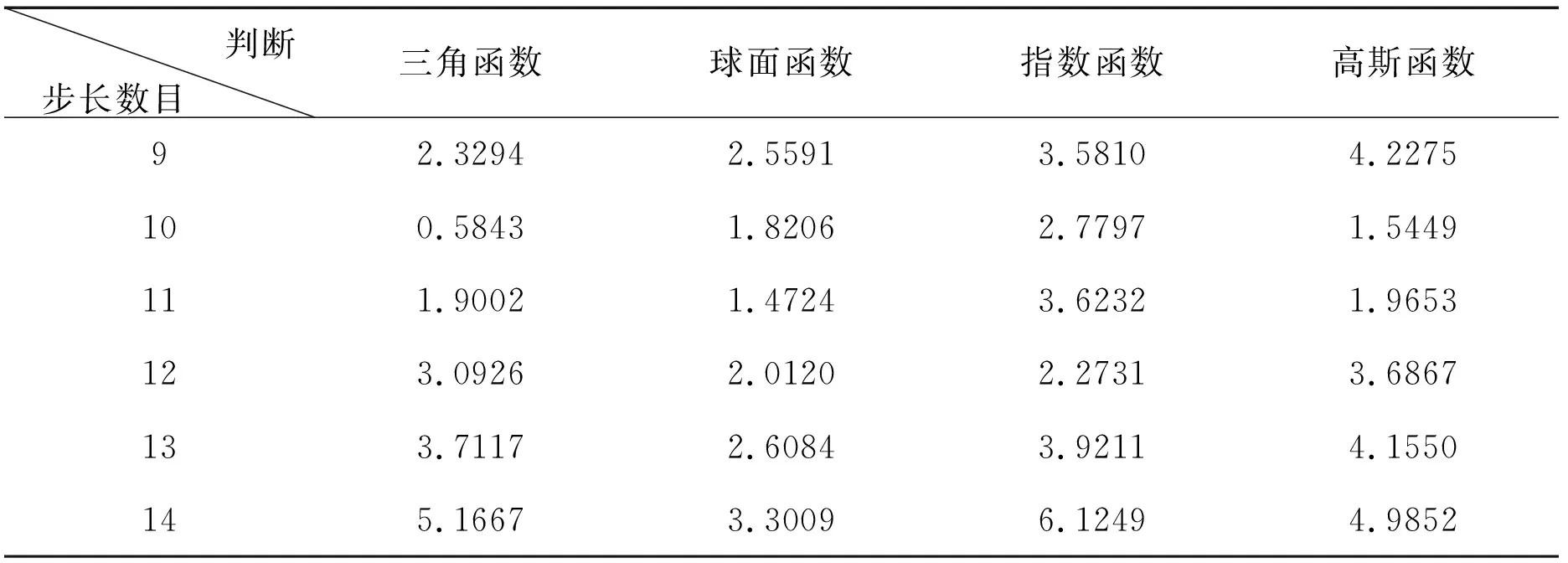
表2 普通克里金法最优步长数目交叉验证公式判断结果
4.2.2 简单克里金插值法
探索性分析确定的最优步长数目为20、21左右,再根据多次试验结果,确定研究最优步长数目范围为16-21。与上述方法一致,用公式判断得出四种半变异函数模型的最优步长数目均为21(表3)。
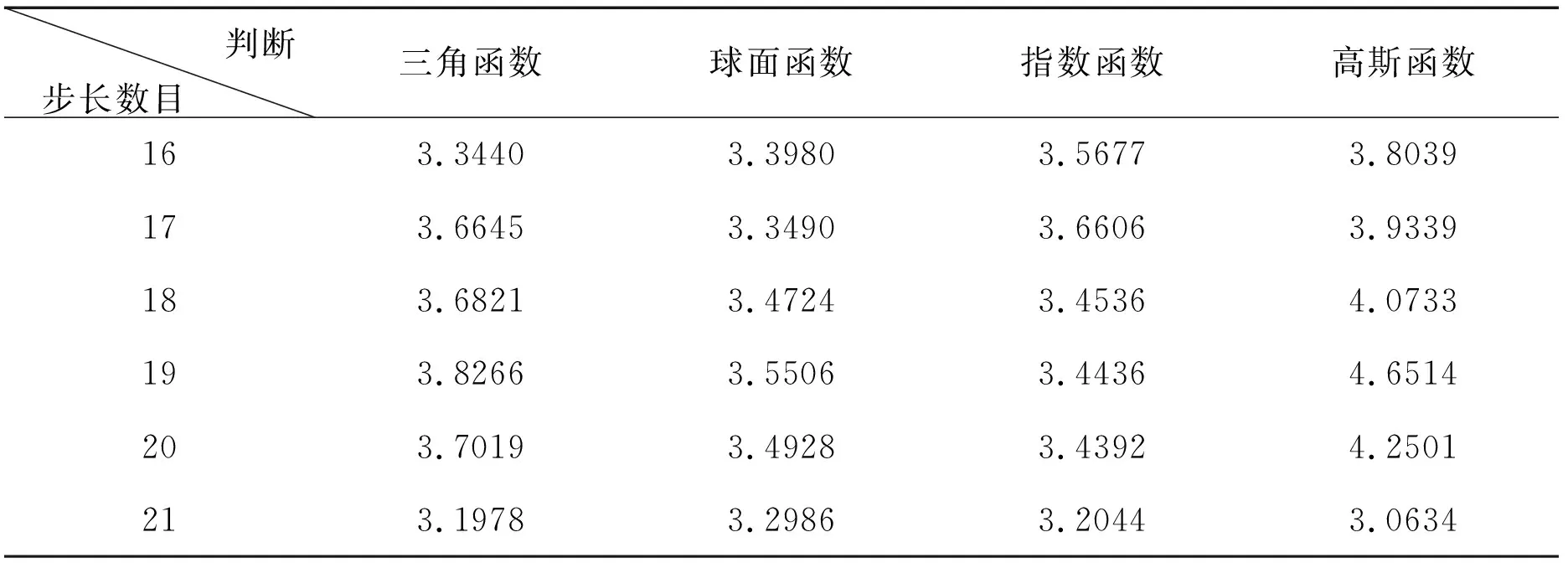
表3 简单克里金法最优步长数目交叉验证公式判断结果
4.2.3 协同克里金插值法
探索性分析确定的最优步长数目在7、8左右,经过多次试验,在插值过程中发现指数函数模型的预测误差明显大于其余三种,因此只对剩余三种模型进行了最优步长数目比较。对于三角和球面函数模型,最优步长数目范围在11-16,高斯函数模型最优步长数目范围在6-11。与上述方法一致,先用公式判断得出三角、球面和高斯函数模型的最优步长数目为11、12和8(表4)。
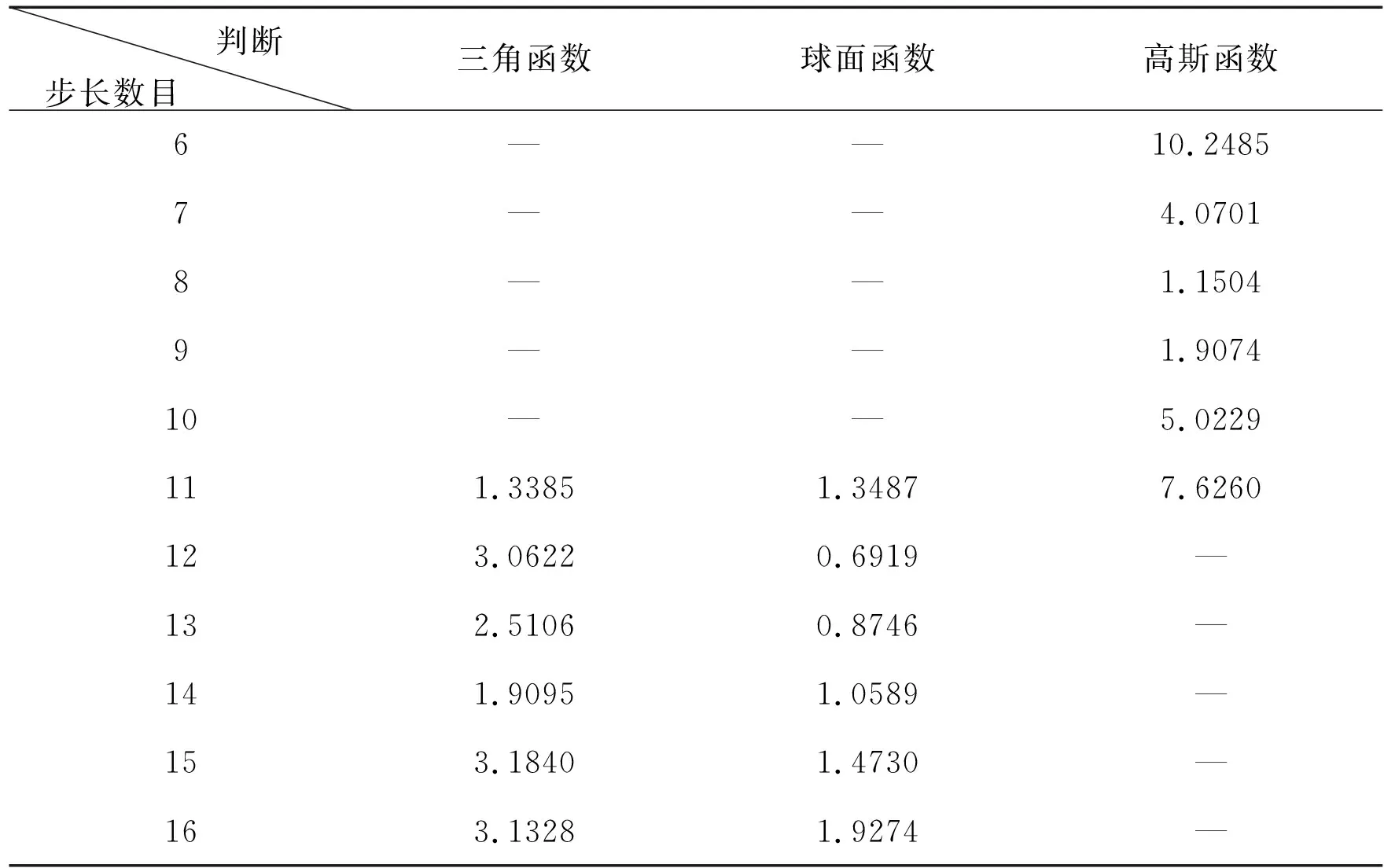
表4 协同克里金法最优步长数目交叉验证公式判断结果
4.2.4 泛克里金插值法
探索性分析确定最优步长数目为12、13左右,但经过大量试验发现泛克里金最优步长数目范围在5-10。与上述方法一致,用公式判断得出三角、球面、指数和高斯函数模型的最优步长数目为7、5、5和8(表5)。
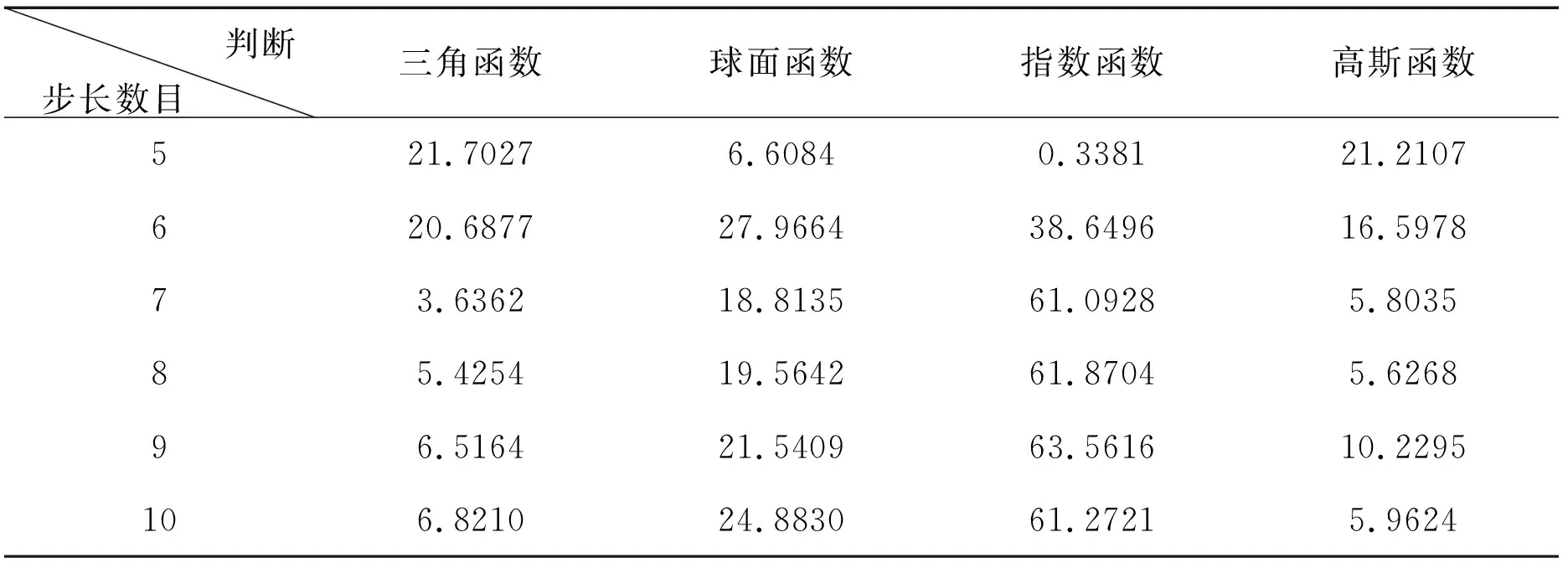
表5 泛克里金法最优步长数目交叉验证公式判断结果
4.3 半变异函数模型比较
现在进一步分析在最优步长数目的情况下,最优的半变异函数模型。通过交叉验证判断公式初步得出普通、简单和协同三种克里金法分别对应的最优半变异函数模型均为高斯函数模型(表6)。插值结果如图5-图7所示。

表6 不同克里金法的最优半变异函数模型交叉验证公式判断结果
从图5插值结果看,高斯函数模型的插值结果图插值高程多集中在中等范围,而且交错地带较少。综合来看,使用普通克里金法时高斯函数模型最优。
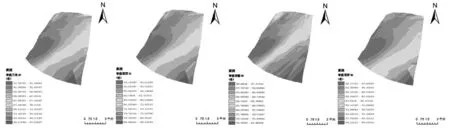
(1)三角函数 (2)球面函数 (3)指数函数 (4)高斯函数图5 普通克里金四种半变异函数模型最优步长数目条件下插值结果图
从图6可以看出,高斯函数模型插值结果图左上角没有牛眼现象,效果较其他三者明显更好。简单克里金法最优半变异函数模型为高斯函数模型。
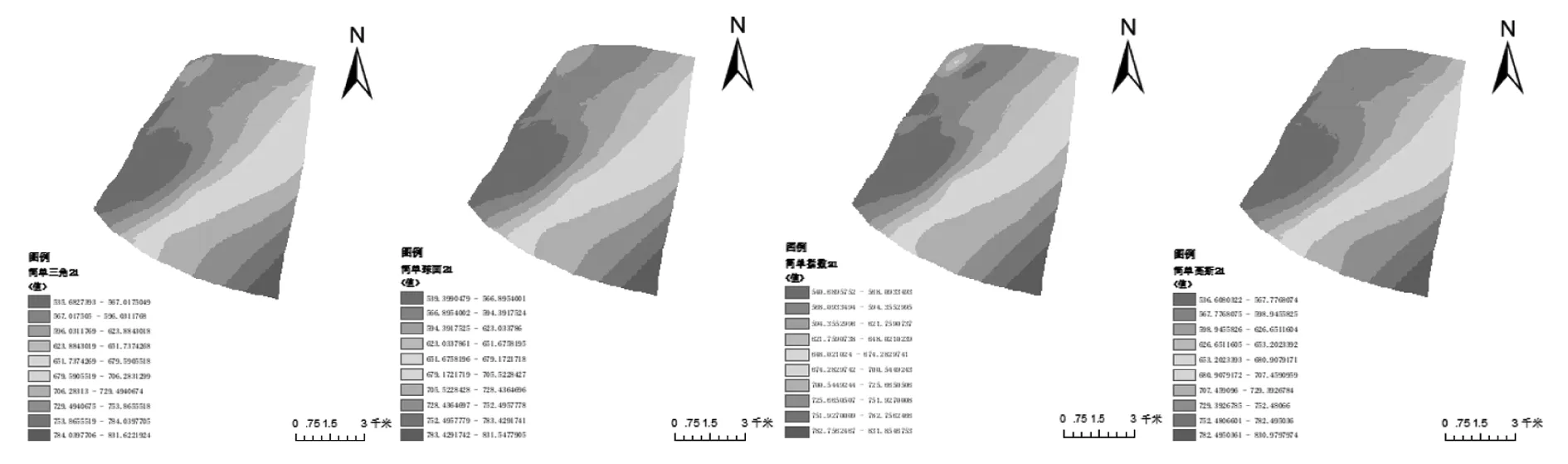
(1)三角函数 (2)球面函数 (3)指数函数(4)高斯函数图6 简单克里金四种半变异函数模型最优步长数目条件下插值结果图
如图7所示,高斯函数模型插值结果交叉带较前两个模型少。综合两方面,以预测误差最小为主要准则,确定协同克里金法的最优半变异函数模型为高斯函数模型。

(1)三角函数 (2)球面函数 (3)高斯函数图7 协同克里金三种半变异函数模型最优步长数目条件下插值结果图
4.4 克里金插值方法比较
在确定了三种克里金方法下的最优步长数目以及最优半变异函数模型之后,确定针对本次研究数据最优的克里金插值方法。利用交叉验证判断公式判断交叉验证五个参数,可初步得出最优克里金插值方法为协同克里金(表7)。

表7 不同克里金插值方法的交叉验证结果
从插值结果的统计特征来看,三种克里金插值方法的插值范围分别为500.50m-893.74m、482.14m-879.94m以及471.57m-910.90m,三者插值范围均合理,而协同克里金法的插值范围明显比其他两个更大。通过选取最优步长数目以及最优半变异函数模型,并经过多层多次对比,以预测误差最小为主要准则,最终确定针对本次研究数据,使用高斯函数模型且步长数目为8的协同克里金插值方法插值效果最优。
5 结论
通过上述的研究过程,得到如下结论:
(1)针对本次研究数据,使用协同克里金插值方法,半变异函数模型为高斯函数模型,步长为8插值效果最好。
(2)无论哪种插值方法,使用高斯函数模型都是最优的。
(3)从半变异函数/协方差云的最优步长数目判断和交叉验证人眼判断以及插值结果统计特征,再加上插值结果图的四方面综合来看,交叉验证时将五个参数根据最优条件进行线性相加,即交叉验证判断公式能够较好反映预测误差好坏,在交叉验证各项指标都很接近的情况下,给出数字表征的最优解。
(4)在研究数据较少,但其与其他数据存在较大相关性时可以使用协同克里金法,能够较大程度上提高插值精度。

