颗粒- 水两相流在直角弯管中的冲蚀特性数值模拟研究

何泽海 何金桥

（ 1、中国电建集团成都勘测设计研究院有限公司，四川 成都610072 2、长沙理工大学能源与动力工程学院，湖南 长沙410114）

冲蚀过程， 是指液体工质中夹带的固体颗粒与流动管道壁面发生接触，并致管道壁面发生损耗，该现象是导致流体输运管道发生破损或失效的重要因素之一[1-2]。 锅炉管路作为流体工质输运通道，是整个锅炉本体的高压边界，管路系统的可靠性，对整个锅炉系统的稳定安全运行具有重要意义。 已有文献记录表明，锅炉管道事故中，约有三分之一的事件为液相中夹带固体颗粒在固体壁面上冲击、切削等作用导致的冲蚀而引起，尤其是弯头结构形式导致该局部区域流动较为复杂，颗粒与金属壁面作用更为强烈，导致弯管的冲蚀比直管严重50 余倍[3]。 目前，国内外许多学者对管道内流动冲蚀问题进行了相关研究，以更好的认识冲蚀机理和主要影响因素，并为缓解管道冲蚀、提高管道输运过程的可靠性提供必要的技术支撑和预测评估方法。 计算流体力学是一种可靠的数值分析方法，可利用其从多种角度针对液固两相流冲蚀过程进行能够有效的数值模拟分析，并对其影响因素进行对比分析，以获得关键影响因素，例如流体运行参数、颗粒类型及尺寸、管道结构等。 Edwards 等人[4]对弯管及三通内的流动冲蚀进行了数值模拟分析，并提出相关缓解措施进行了分析。 曾莉[5]、胡跃华[6]、胡宗武[7]等对管道内冲蚀磨损的机理和水力特性进行了模拟研究和分析。 这些研究对冲蚀磨损的预防具有参考价值。本文采用计算流体动力学（ CFD）方法，对固- 液两相流体在90°直角弯管内管壁上的流动冲蚀特性进行数值模拟分析，以获得颗粒参数和属性、流动参数等因素对内壁面冲蚀磨损的影响规律。

1 物理模型

本文研究的对象属于液固两相流动，除了CFD 的基础模型之外， 主要采用的物理模型涉及到液固相的作用力和冲蚀模型，分别如下所述。

1.1 曳力：Schiller-Naumann

其中，α：微小颗粒相对壁面的入射角；ReP：微小颗粒的雷诺数；Vs：微小颗粒的滑移速度，m/s；Dp：微小颗粒直径，m。

1.2 流动冲蚀模型

固体材料类型、颗粒尺寸、颗粒入射角度、颗粒速度等因素是影响固液两相流冲蚀的重要参数。 流动冲蚀模型是建立在实验的基础上并耦合进CFD 计算程序中，本文主要采用使用较为广泛的Ahlert 模型和Oka 模型。 Oka[8-9]和Ahlert[10]等均围绕颗粒直径、入射角度、颗粒滑移速度等影响因素提出了描述流动腐蚀速率的数学模型。

1.2.1 Ahlert 模型

Ahlert 模型通过实验对测量碳钢和铝材管道的磨损情况，给出了其磨蚀模型，其模型与管道材料、颗粒速度、颗粒形状(球形、尖角型等)、碰撞角度有关。

其中，K：依赖于材料的常数；Fs：与微小粒子形状相关的因子（ 或形状因子）；含有尖角的颗粒取值为1;半球体颗粒取值为0.53；球体颗粒为0.2；α：微小颗粒相对壁面的入射角；f(α)：入射角的函数；Urel：微小颗粒相对于壁面的速度；N：常数；X，y，ω：用户定义；z：根据连续相的入射角函数获得。

1.2.2 Oka 模型

Oka 模型同样根据实验数据开发得到，并对冲蚀磨损的因素进行了更多的考虑，其影响因素还包括管道材料Vickers 数(表征材料硬度)、相对速度、颗粒直径等。

其中，α：微小颗粒相对壁面的入射角；g(α)：入射角的函数；e90: 颗粒入射角为90°下的腐蚀速率；n1、n2、Hv： 用户自定义常数，其中Hv表征腐蚀材料的维氏硬度，单位为GPa；Urel：微小颗粒相对于壁面的速度，m/s；Uref：用户定义的参考速度，m/s；Dp：微小颗粒直径，m；Dref：用户定义的参考直径，m。

2 几何结构与网格

计算分析中， 采用常见的90 度直角弯管作为分析对象，直管段内径为100mm，弯管半径取2 倍直管内径，即200mm，流体入口流动方向与重力方向相同， 直角弯管结构和边界条件选择如图1 所示。

图1 直角弯管结构示意图

计算中采用结构化网格进行计算域的空间离散，圆管横截面网格分布如图2-a 所示，采用O 型网格方法，沿管程方向采用拉申方法建立网格。

图2 直角弯管结构示意图

考虑到弯管及下游区域流动的复杂性，在进行网格敏感性分析时，沿流动方向的网格数量不进行尺寸调整，均采用100 层网格，只要对横截面方向的网格尺寸进行敏感性分析。首先需要进行网格无关性验证。计算中对比了3 种网格数量，表1 给出了不同网格尺寸方案的网格总数和物理参量对比结果。可以看出，当网格数为33 万时，管道内流动冲蚀速率与管道总体流动压降已与88 万网格相差不大，如图3 和图4 所示。因此采用33 万网格时，从计算经济性和准确性上均较为理想，后续计算分析均用33 万网格。

表1 网格方案敏感性分析结果对比表

计算中，入口液相的流速为5m/s，管道壁面采用316L 不锈钢。

3 数值模拟结果与讨论

3.1 磨蚀模型对比

图3 磨蚀率随网格数的变化曲线

图4 管道流动压降随网格数的变化曲线

本文计算分析了固体颗粒在工质水中的流动及对壁面的冲蚀过程。在磨蚀模型方面对比了Ahlert 模型和Oka 模型在相同条件下的磨蚀率差异。如前所述，Ahlert 模型通过实验对测量碳钢和铝材管道的磨损情况，给出了其磨蚀模型，其模型与管道材料、颗粒速度、颗粒形状(球形、尖角型等，)、碰撞角度有关。Oka 模型同样根据实验数据开发得到，并对冲蚀磨损的因素进行了更多的考虑，其影响因素还包括管道材料Vickers 数(表征材料硬度)、相对速度、颗粒直径等。

计算中其他边界条件均一致，图5 给出了分别采用两个模型时管道内壁冲蚀率的云图分布，此时颗粒直径为0.5mm，颗粒密度为7832kg/(m3*s)。从结果中看出，采用两种模型所得到的内壁冲蚀速率分布和主要冲蚀区域均基本相同，但是在磨蚀速率方面，Ahlert 模型的最大冲蚀速率为0.043kg/ (m2*s)，Oka 模型则为0.00041 kg/ (m2*s)，表明Ahlert 模型的磨蚀速率要显著高于Oka 模型。分析认为，这主要是由于Ahlert 模型主要基于碳钢和铝材模型开发得到，而本文计算管道材质采用了316L 不锈钢，导致Ahlert 模型得到的冲蚀速率预测结果偏高。因此，考虑到Oka 模型基于的实验数据宽泛性以及更全面的影响因素，后续计算分析中，已Oka 模型为主。

图5 相同颗粒直径时不同冲蚀模型的对比图

图6 采用Oka 模型时不同颗粒直径对冲蚀量的影响

图7 不同颗粒直径下颗粒分布及速度大小示意图

图8 不同颗粒直径下颗粒分布图

3.2 颗粒直径对比

颗粒直径大小决定了颗粒与流体工质的相互作用，会对其运动轨迹及相对速度产生影响，同时粒径大小还会影响自身的质量大小，从而决定其与管道壁面作用大小，如碰撞过程，最终影响壁面冲蚀的强度。本文分析了直径在0.05-2mm 范围内的颗粒对壁面冲蚀速率的影响差异，以分析不同粒径的冲蚀特性。

图6 给出了6 种颗粒直径下，得到的管道内壁冲蚀率云图分布情况，计算中入口的固体颗粒速度和材料相同，总质量也相同，即颗粒直径越大，颗粒数量越少。从内壁面冲蚀速率观察表明，颗粒直径越大，颗粒自身质量越大，受流体的作用而发生的流动轨迹变化越小，此时流动冲蚀主要集中在弯管底部区域，如d=2mm 时，局部最大冲蚀率为3.1E-3kg/( kg/(m2*s))，当d=0.05mm 时，局部最大冲蚀率降低为7.5E-5kg/( kg/(m2*s))。随着颗粒直径的逐渐减小，颗粒自身惯性力逐渐减小，在弯管处受复杂流场的影响增强，导致颗粒在流场中的分布更均匀，最终使管道内部的磨蚀面积进一步增大，而局部冲蚀率则减弱。

颗粒直径变化对冲蚀率的影响也可以从颗粒速度及分布情况两方面进行分析。图7 中给出了不同颗粒直径下，流体域内颗粒的分布情况，图中颗粒自身的参量色差表示速度大小。可以看出，当颗粒直径较大时，颗粒主要集中分布在弯管底部区域，即发生冲蚀的主要区域。随着颗粒直径的减小，颗粒随流动的跟随性更强，颗粒在弯管及下游分布更均匀，且速度分布也更均匀，基本与主流流体速度一致。从图8 中可以看出，随着颗粒直径的减小，颗粒在流场中的相份额分布更均匀，说明了更小颗粒直径具有更大冲蚀面积的原因。

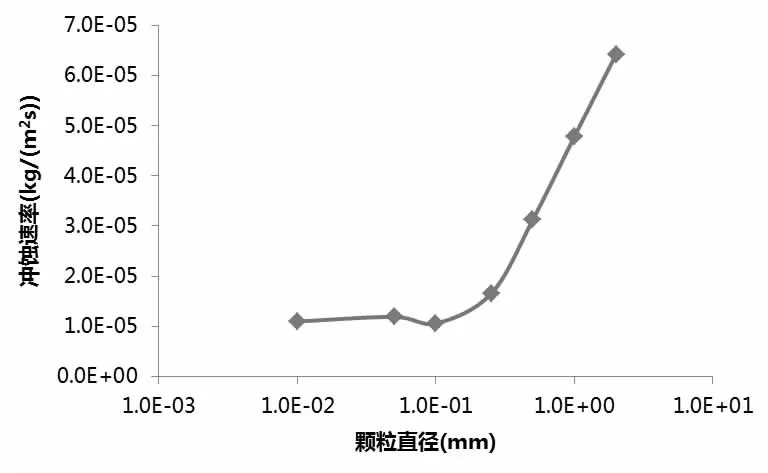
图9 颗粒直径对冲蚀速率的影响

通过提取不同直径下内壁面冲蚀速率的均值，如图9 所示，随着颗粒直径的增加，内壁面冲蚀速率迅速上升，这与沈雅欣等人[11]对90 度直角弯管内颗粒直径对弯管冲蚀速率的实验测量规律相一致。

3.3 颗粒密度对比

在实际情况中，管道输运工质中可能包含不同材料种类的固体颗粒，由于密度大小不同，对其惯性力大小产生差异，因此导致其对管道内壁的冲蚀强度存在差异。本文计算中考虑了5种不同颗粒密度进行了对分析，主要涵盖了金属型颗粒(密度大于4000 kg/(m3s))、非金属型颗粒(密度小于2000 kg/(m3s))两大类。

计算中颗粒直径取0.5mm，通过计算对比，发现对于密度大于4000 kg/(m3s)的固体颗粒，密度越大，局部冲蚀速率越高，此时由于颗粒质量较大，流体难以使颗粒运动轨迹发生明显改变，发生磨蚀的区域主要集中在弯管底部。当密度小于2000 kg/(m3s)，颗粒在流场中的分布区域更均匀，使管道内壁的磨蚀也更加均匀，而非集中于弯管底部区域。这一规律与更小直径颗粒的规律相似，说明单一颗粒的个体质量降低，会进一步提升颗粒在弯管内的分布均匀性，降低局部冲蚀情况。

还需注意的是，当颗粒密度小于1000 kg/(m3s)时，此时颗粒所受浮力作用明显，改变了颗粒的运动特性，使颗粒集中于弯管内侧，并使该区域的局部冲蚀率偏高，但从总的冲蚀速率看，如图10 所示，其冲蚀率仍处于可接受范围。同时，从图10 中可以看出，随着颗粒密度的增加，管内冲蚀率逐渐增加。

4 结论与建议

图10 采用Oka 模型时不同颗粒直径对冲蚀量的影响

图11 颗粒直径对冲蚀速率的影响

通过本文对直角弯管内的流动冲蚀特效开展的计算分析，可以得到以下几点结论：

4.1 由于Ahlert 与Oka 模型所开发基于的管道材质类型差异，导致磨蚀量存在明显差异；

4.2 颗粒直径对冲蚀的影响体现在磨蚀程度和磨蚀面积两方面，颗粒直径越大，磨蚀区域集中在弯管底部区域，磨蚀量越大，颗粒直径越小，磨蚀区域趋向于管内均匀分布，局部磨蚀量降低，同时磨蚀面积更大、更均匀；

4.3 颗粒密度变化会会改变颗粒重力与浮升力的综合作用方向，结合弯管内流场的局部压力梯度，密度越小，颗粒会聚集于弯管内侧，且磨蚀较小，密度增大，颗粒会加剧弯管外侧的磨蚀，且密度越大，磨蚀区域越集中、局部磨蚀量越大。