风电功率时间分层组合预测优化方法

王尚斌，王立峰，李洪海，任兴辉，王 楠

（1.山东鲁能软件技术有限公司，山东 济南 250002；2.国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

风电功率预测按时间长度可分为超短期、短期、中长期预测［1］，从电网调度角度来说，上述预测结果分别用于实时调度、日前调度和检修计划、年度发电计划等［2-3］。不同时间尺度的风电功率预测，关注的侧重点不同，利用的信息和统计方法亦不同，如风电功率中长期预测关注时间序列里起长期作用的因素，短期和超短期预测关注时间序列里起短期作用的因素［4-9］。因此，不同时间尺度风电场功率单独预测结果往往不一致，进而导致调度决策不一致。如以15 min 为间隔的风电功率预测值汇总得到的未来4 h 预测结果，与以1 h 为间隔的风电功率预测值汇总得到的未来4 h 预测结果，功率变化趋势等往往不同，导致调度决策不一致；如以周为单位的预测值汇总得到年度功率预测曲线，与以月为单位的预测值汇总得到年度功率预测曲线差异较大，会影响检修计划、年度发电计划制定等。

解决以不同时间单位为频率进行预测时，因利用信息和统计方法差异导致预测结果不一致的相关研究，最早可追溯至1972 年［10］。文献［10］中开创性研究了时间聚合对单变量时间序列模型的影响，提出基于聚合模型的预测结果要优于非聚合模型预测结果。

在2009 年之前的大多数文献，一般采用在单个层级生成预测，然后再聚合的方法［11］。例如，自下而上法（Bottom Up，BU）预测只在最底层生成，然后汇总到层级结构中的更高层级。文献［12］提出组合预测的方法，用以解决单层级预测结果聚合过程中信息丢失的问题。文献［13］对文献［12］中的方法进行了优化，提出每个层级的预测形成“原始”或“基础”的预测结果，对所有层级预测结果加权组合，确保整体层级预测结果的一致性。文献［14］在上述研究成果的基础上，第一次明确提出时间层级结构的概念及时间层级预测方法。时间层级预测首先在不同时间层级利用对应信息分别进行基础预测，再基于时间的层级结构对各层级基础预测进行整合和优化，得到各时间层级预测结果的修正值，并使预测结果满足一致性要求。

在时间分层组合预测方法的基础上，分析现有方法在时间分层预测校正时的不足，并引入交叉验证（Cross-Validated，CV）思路予以改进；将交叉验证算法应用到风电场不同时间尺度的功率预测中，对比传统方法，为提高不同时间尺度风电功率预测结果一致性和功率预测精度提供新思路。

1 时间分层组合预测方法

1.1 时间分层结构

以15 min 为采样间隔对风电功率时间序列进行分析，将其聚合为采样间隔为1 h 和1 d 的时间序列，如图1 所示。

从下到上3 个层级的时间序列，可用于超短期、短期和中长期的风电场功率预测。需要特别指出的是，图1 仅表示时间层级结构，层级数量和每层时间序列的采样间隔可根据实际情况进行调整。

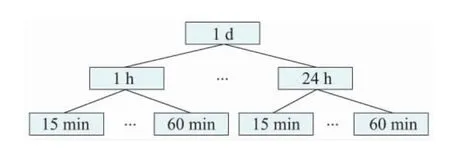
图1 时间层级结构示例

层级数量的改变，只影响层级结构聚合的次数，每层时间序列采样间隔的改变，只影响每层结构节点的数量，不影响时间层级组合方法的应用。如图1中，将第2 层采样时间间隔聚合为30 min，不影响时间层级组合方法的应用。

1.2 时间分层组合预测

首先，定义一个多时间层级序列｛yt｝，t=1，2，…，T，T 是时间序列的观测时长。设m 为时间层级结构中最底层时间层级的采样频率，可知T 是m 的倍数。设k 是每个时间层级中包含最大采样频率时间序列的个数，k 为整数，可知k 是m 的约数，由｛k｝组成了最完整的时间层级结构。

以图1 为例，m 为1 d 时间内风电功率采样频率，m=96。假设采样时长为1 年，则观测时长T=m×15×365，同时，可知最完整的时间层级k ∈｛96，48，32，24，12，8，6，4，3，2，1｝。在图1 中共有3 个层级，k∈｛96，24，1｝。令i=1，2，…，T／m，i 表示1 年内不同的观测日，令p=1，2，…，m／k，p 表示1 d 内每个层级的节点变化，时间序列｛yt｝中每个层级的节点值可表示为

图1 所示的时间层级结构，具体表示如图2 所示。

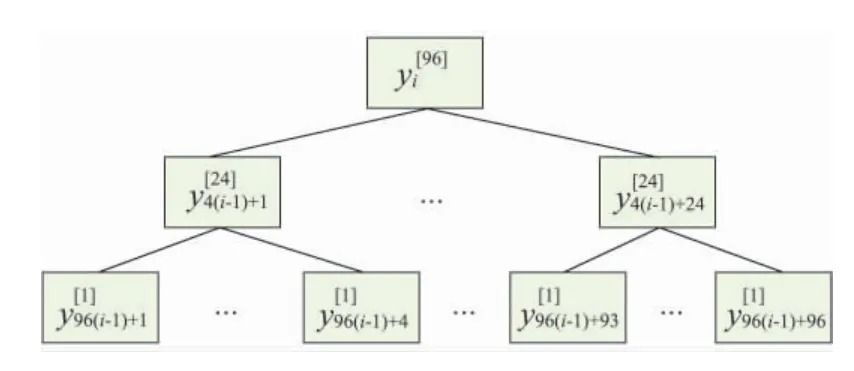
图2 采样间隔为15 min、1 h 和1 d 时间序列的风电功率分层预测结构

对于时间段i 内每个时间层级，可表示为

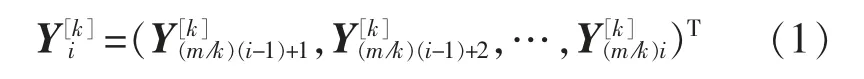
令｛l｝表示降序排列的m 的因子集合，则kl=m，k1=1，从而时间序列可进一步表示为

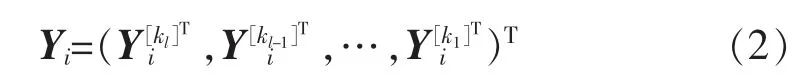
S由子矩阵Sk堆叠而成，而子矩阵Sk可通过逐行的复制m／k 大小的单位矩阵每个条目k 次而得到，从而S为Σ（m／k）×m 阶矩阵。当m=96 时，S可由子矩阵S1、S2、S3、S4、S6、S8、S12、S16、S24、S32、S48、S96堆叠而成，S为252×96 阶矩阵。

假设对时间层级结构最底层的风电功率进行h*步的基础预测，则h=1，…，h*／m 为整个层级结构预测步数。各时间层级的基础预测可表示为

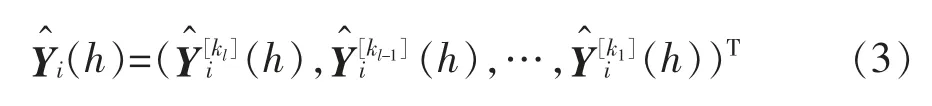
进一步，整个时间层级步的基础预测可表示为

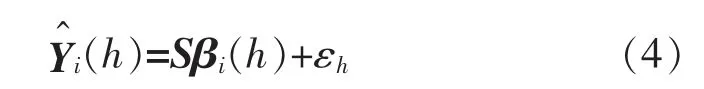
采用广义最小二乘法 （Generalized Least Squares，GLS）估计βi（h），可得：

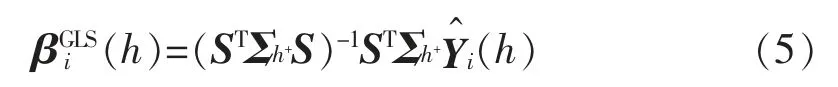
式中：Σh+是Σh的广义逆。

从而，可得到时间层级的组合预测模型

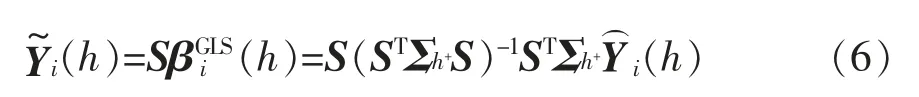
然而，实际中Σh是未知的。为求解Σh，需引入相关参数进行简化，利用的方法主要包括BU、平均底部法 （Bottom Average，BA）、全球平均值法（Global Average，GA）、线性平均值（Lineal Average，LA）、加权最小二乘法 （Weighted Least Squares，WLS） 等方法。

文献［13］中，Wickramasuriya 等人引入最小值估计量，即单步长基础预测误差协方差。即

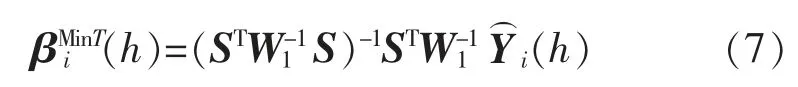
其中，

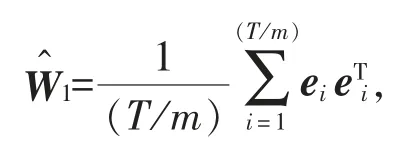
ei为单步长基础预测误差，即

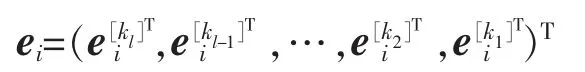
基于时间层级结构采用WLS 法，则

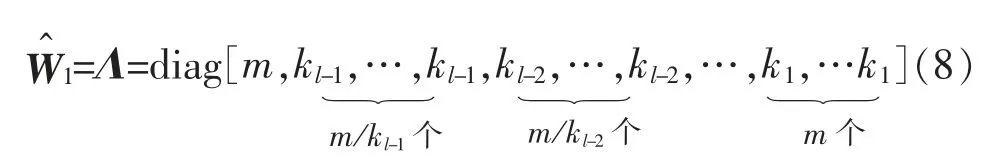
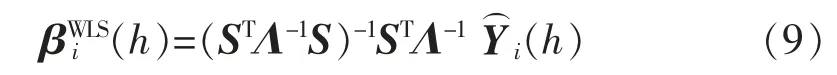
从而，

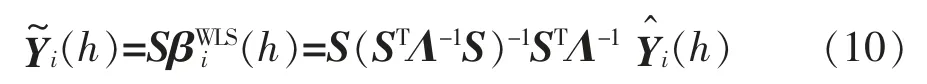
直接估计较Λ为复杂，文献［14］中Athanasopoulos 等人将Λ进一步简化为3 种对角矩阵：层级方差尺度矩阵ΛH、方差尺度矩阵ΛV和结构尺度矩阵ΛS。由于Λ为对角矩阵，非对角元素均为零，在采用上述方法进行预测时，不同时间层级结构的信息数据会丢失。

1.3 改进时间组合预测方法

为解决引入相关参数以简化求解时间层级组合预测模型Yi（h）过程中，不同时间层级结构的信息数据丢失的问题，提出一种采用CV 求解Yi（h）最优解的方法，可保留不同时间层级更多信息数据，使预测结果在各时间层级具有更好的一致性和更高的精度。

采用如下方法求解矩阵P：

1）将多时间层级序列｛yt｝分为不重叠的3 部分，训练集｛yt｝train、验证集｛yt｝val、测试集｛yt｝test。

2）使用训练集｛yt｝train中数据估计模型参数，并将这些估计值表示为～θtrain。引入累计分布函数（Cumulative Distribution Function，CDF），对验证集｛yt｝val中每个时间层级进行t+h 步的预测，得到未组合的预测累计分布函数。由左乘投影矩阵SP后，得到用于组合预测累计分布函数。

上述方法中，交叉验证目标函数值为

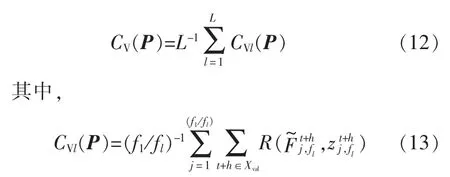
式中：fl为第l 时间层级对应的元素个数；L 为时间层级的层数；Xval为验证集中的样本。

由于矩阵P很大（96×121 阶矩阵），提出矩阵P的一种稀疏结构。以为f=［4，2，1］例，矩阵P可采用以下稀疏结构优化。

式中：vrl为时间层级l 中第r 个元素的权重。

在交叉验证过程中，考虑3 种情况对PCV中权重进行约束：PCV中所有元素为正，且每行元素之和为1；PCV中每行元素之和为1；PCV中所有元素无约束。

采用CRPS 函数作为评分规则，其中：

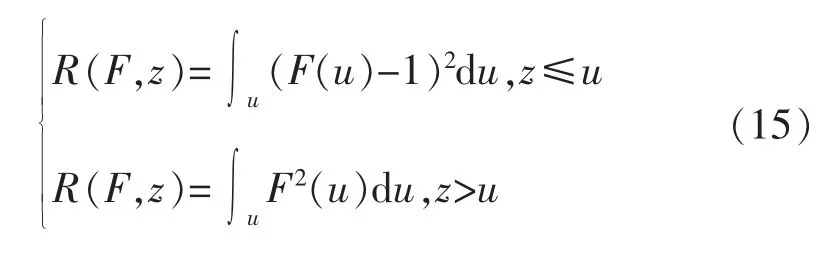
2 方法应用分析

为验证方法的效果，选择山东电网装机容量49.5 MW 的某风电场，2018 年10 月至2019 年9 月每15 min 时间序列的风电出力数据，进行应用研究。

首先，将12 个月的风电出力观测数据按6：3：3时间比，分为训练样本数据、验证样本、测试样本。即将2018 年10 月至2019 年3 月共计6 个月的风电出力数据用作模型训练，对各时间层级的风电功率概率预测模型进行训练；将2019 年4 月至2019年6 月共计3 个月的风电出力数据用作模型验证，对每个时间层级中概率预测结果进行交叉验证得到权重；将2019 年内7 月至2019 年9 月共计3个月的风电出力数据用做测试和评估模型的泛化能力。

然后，将时间序列按15 min、1 h、4 h、24 h 分为4 个层级，即f=［96，24，6，1］，对每个时间层级的风电功率进行单独预测，得到基础预测值。时间层级和预测方法如表1 所示。

表1 风电场各时间层级预测模型

采用所述交叉验证方法，基于验证样本数据，优化PCV不同约束下的权重。即PCV采用式（14）中的稀疏结构，以式（12）为目标函数，对表1 中各时间层级模型的预测结果进行修正。各时间层级不同约束下的权重均值如表2 所示。

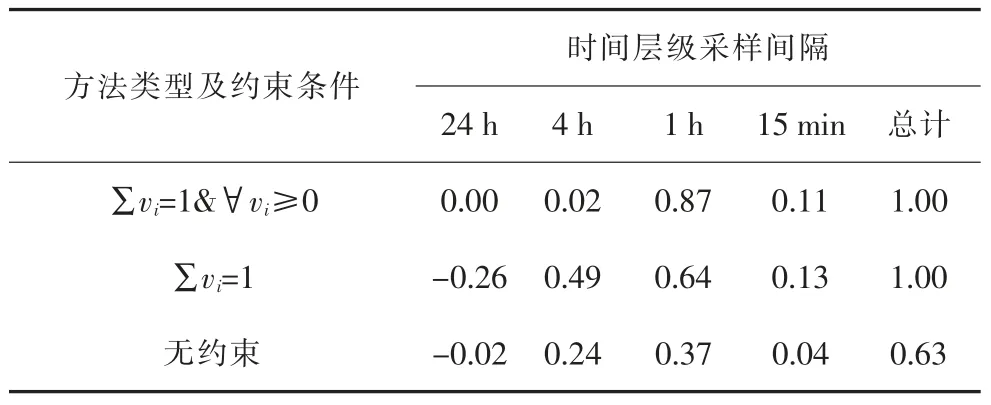
表2 各时间层级不同约束下的权重均值

在测试集｛yt｝test中，基于BU、BA、GA、LA、WLS、CV 等方法，对每种方法下每个预测原点127 （96+24+6+1） 个节点的风电功率预测值的CRPS 值进行评估。这些值在｛yt｝test中取均值，然后在每个时间层级中所有节点上再次取均值，得到表3 中第2—5 列的数据。表3 最后一列为时间层级结构中，每个层级CRPS 平均值的平均值。CRPS 越小，方法在时间层级结构的聚合约束效果越好。不同方法下，时间层级结构中每个层级CRPS 平均值如表3 所示。

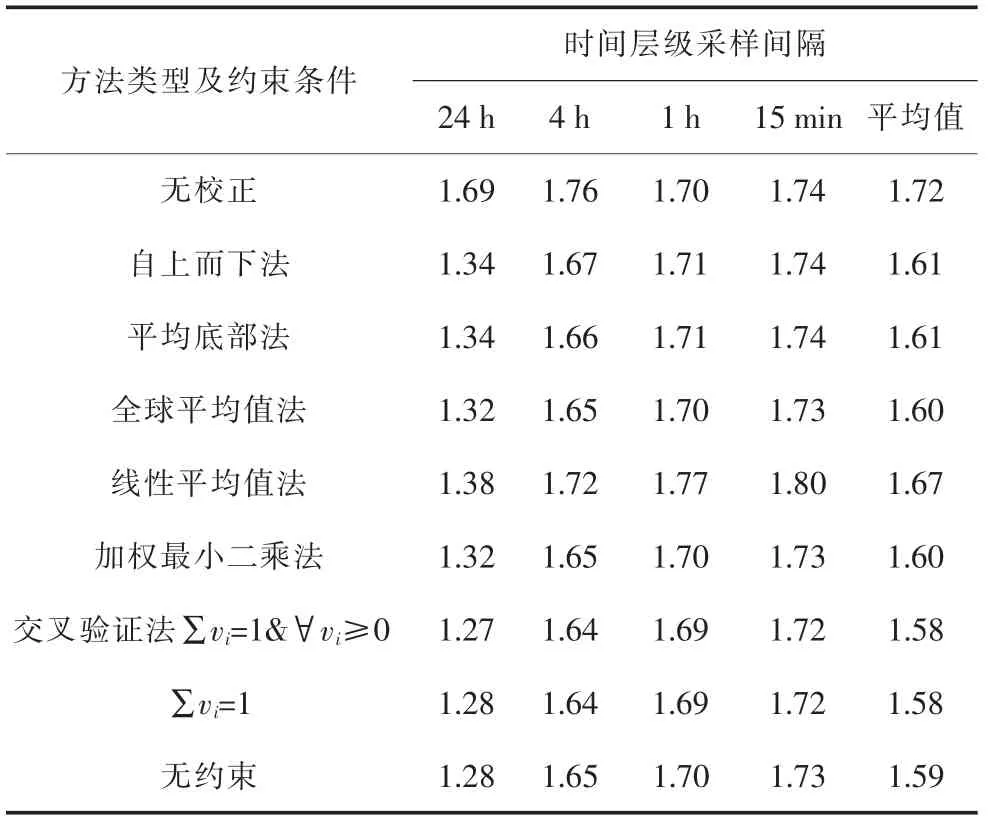
表3 时间层级结构中每个层级CRPS 平均值

由表3 可知：

1）基于时间层级结构，无论选择哪种组合预测方法对基础预测进行调整和优化，其预测结果的聚合约束均优于独立预测。

2）时间层级组合预测方法中，对采样间隔较大的时间层级优化效果优于采样间隔较小的时间层级，即时间层级组合预测方法对采样间隔较大的时间层级预测精度的提升，较采样间隔较小的时间层级更加明显。

3）提出的交叉验证方法预测结果的一致性优于其他常规组合预测方法。

3 结语

介绍时间分层组合预测的概念以及相关方法，针对目前组合预测方法中协方差估计困难，提出一种交叉验证时间分层组合预测方法，通过优化尺度缩放矩阵P的结构，保留不同时间层级结构更多信息。

对风电场实际功率数据进行预测的结果表明，交叉验证时间分层组合预测方法，可有效提升各时间层级尤其是采样间隔较大时间层级的预测精度，其预测结果较其他常规组合预测方法的一致性更佳。