基于Shapley 值的园区分布式综合能源系统利益分配研究
闫庆友,于振华
(华北电力大学经济与管理学院,北京 102206)
0 引言
在环保压力加剧、能源供应紧缺的状况下,提高能源利用效率、实现能源互联互通、保障可再生能源消纳成为必然选择。综合能源系统作为一种人类社会能源的承载形式,可以实现多种类型的能源耦合,灵活接入和消纳分布式能源,逐渐进入人们视野。国家电网有限公司在确定了向综合能源服务商转型的战略后,于2020 年又进一步确立了“建设中国特色国际领先的能源互联网企业”的新战略[1],其中能源互联网在功能上要实现“源网荷储”协调互动,保障综合化服务需求,综合能源系统已经成为未来能源系统的发展方向[2-3]。伴随着综合能源系统研究的逐步深入,相关业务服务将产生新产业、新业态,形成不同的商业模式。园区的能源需求包括冷、热、电等多种形式,并且园区本身具备各种分布式电源之间的互联条件,因此成为分布式综合能源系统的重要应用场景[4]。随着电改的逐步深入,电源运营主体向用户直接售电成为可能。园区内各参与主体如何在协同优化配置资源的同时保障各方利益,成为促进分布式综合能源系统建设的重要研究内容。
关于综合能源系统收益分配,目前已有研究侧重于非合作模式下的收益问题或仅考虑部分主体的收益。例如杨峥等[5]针对三方市场主体,提出了以能源运营商为主体的市场交易框架,建立了三方理性追求自身利益最大非合作博弈模型。马恒瑞等[6]建立了储能参与调频服务的区域综合能源运营优化模型,保证了电能与调频服务市场总体利润最大。王旭东等[7]从整体角度出发提出了多主体商业运营模式,但未考虑整体收益如何分配至各参与主体。薛金花等[8]提出了3 种光伏运营模式,并分析了用户及能源投资商在不同运营模式中的效益,但并未考虑用户负荷和光伏系统之间的联系。WANG 等[9]针对多能交易问题,提出一种基于分层Stackelberg 博弈模型用以解决交易中各主体的利益均衡问题。LEE 等[10]重点研究了微网间分布式能源交易机制,提出收入按销售额比例进行分配。Shapley 值法具有计算方便、所得解唯一的特点,广泛用于研究供应链利益分配问题,付秋芳等[11]将TOPSIS 与Shapley 值相结合,并将之应用于供应链利益分配。李军等[12]在研究企业协同创新联盟利益分配问题时,对Shapley 值法进行改进,使其联盟更加稳定。Shapley 值近年来也逐渐应用到能源领域,闫庆友等[13]构建了基于Shapley 值的碳排放因素分解模型,并分析了京津冀火电行业碳排放因素。周长城等[14]建立了工业园区综合能源的合作博弈模型及效用函数,但未能建立不同运营模式的收益模型。
鉴于目前研究较多集中在多能系统的单独运营,只追求单方利益最大,对合作模式下的多主体行为和各主体的收益分配研究较少。以分布式综合能源系统为研究对象,针对园区分布式综合能源系统商业模式和运营特点,建立各市场主体在不同运营模式下的收益计算模型;在此基础上,考虑多方主体合作运营的整体利益,运用Shapley 值法对增量收益进行分配;并将其应用到一个由分布式光伏、热电联产和用户三方主体组成的分布式综合能源系统中。
1 园区分布式综合能源运营模式
分布式能源作为一个系统工程,包含众多子系统。如图1 所示,所研究的园区综合能源系统中主要参与的主体包括光伏系统(Photovoltaic,PV)、热电联产联供系统 (Combined Heating and Power,CHP)、分布式储能系统(Distributed Energy Storage System,DESS) 以及园区内的工商业用户(User,U)。其中分布式储能采取恰当的充放电策略,保障园区供电可靠,提高能源利用;光伏和热电联产为园区提供电能,CHP 将低品位的热量为用户供热。
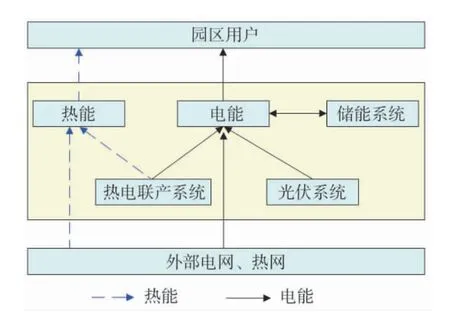
图1 园区分布式综合能源系统能量流动
在合作供能模式下,各参与主体可以组建合作联盟,按照一定规则合理调配各种资源,该模式下的能量流和资金流如图2(b)所示。
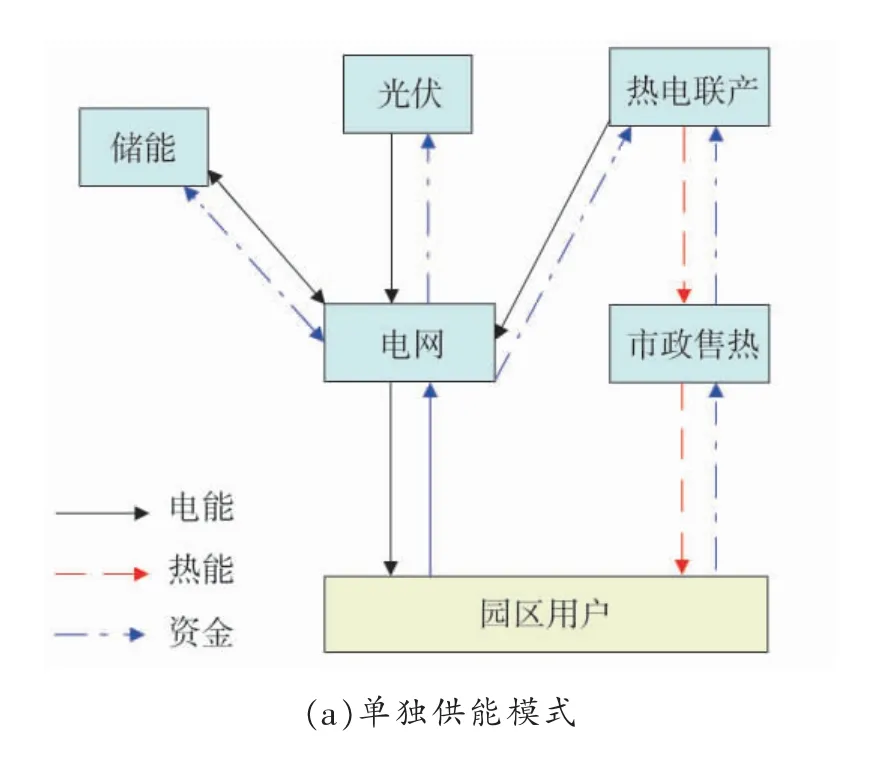
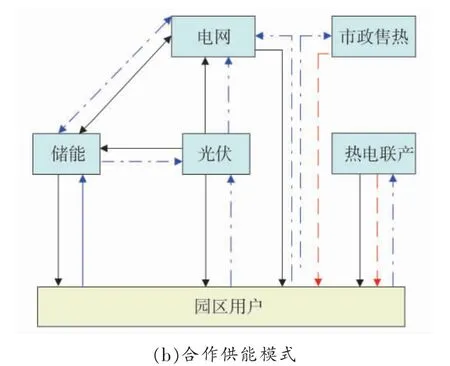
图2 园区各参与主体供能模式
1.1 传统单独供能模式下收益模型
1)储能主体收益:储能在传统的电力系统中不具备规模经济性,在日内未进行充放电操作,所以没有直接的经济收益。即

2)光伏主体收益:在传统独立供能模式下,光伏主体的收益主要来源于光伏全额上网的收益和补贴收益。即
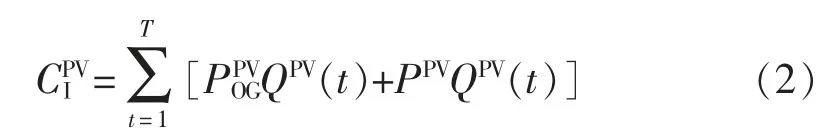
3)热电联产机组收益:由于热电联产机组热出力按成本价出售给市政部门,其收益来源主要是发电全额上网。即
选择培养基,从牦牛酸醡肉中共分离纯化得到乳酸菌11株、芽孢杆菌10株、真菌17株(不排除同种菌),一一编号,保存于4 ℃冰箱备用。
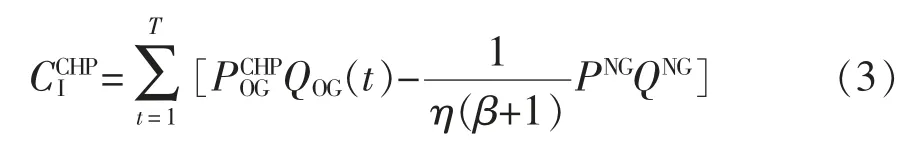
4)用户收益:用户收益主要包括用电和用热所花费用的总和,主要和用能单价和用能负荷有关。即
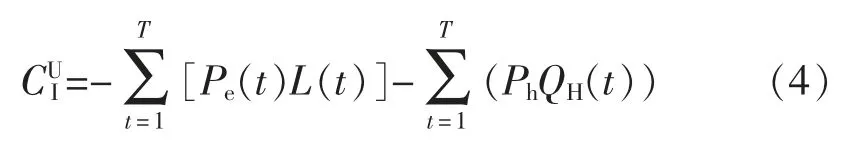
1.2 综合能源合作供能模式下收益模型
1)储能收益:储能收益主要为赚取峰谷价差。即
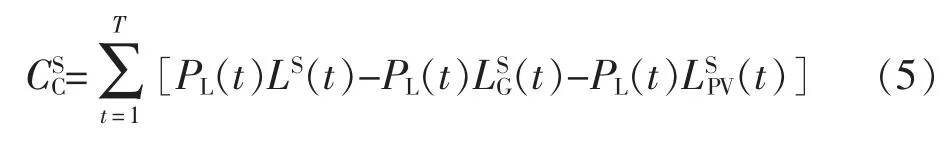
2)光伏收益:主要包括政府补贴、余电上网收益以及出售给储能企业的收益。即
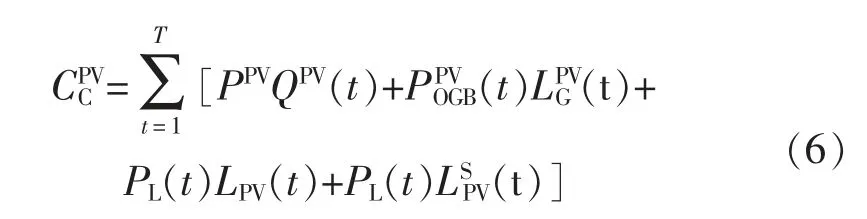
3)热电联产机组收益:主要包括出售给用户的电收益和热收益。即
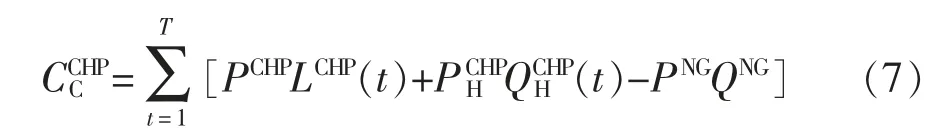
4)用户收益:主要包括购热收益和从热电联产、光伏、储能以及电网的购电收益。即
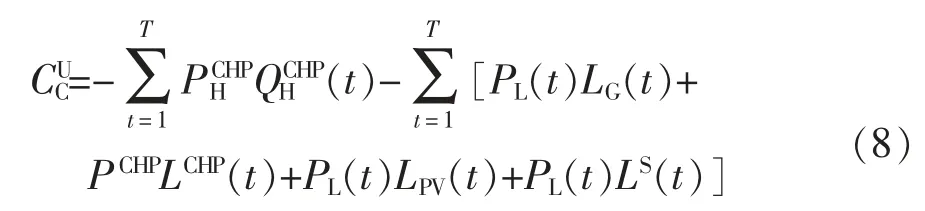
式中:LG(t)为t 时刻园区用户的购电量。
2 基于Shapley 值的区域综合能源系统利益分配
Shapley 值法最早由美国学者提出[15],该方法将联盟成员所应分配的利益与成员贡献相匹配,同时可以体现联盟成员之间的个体博弈,可以体现分配的公平性,被广泛用于解决动态联盟中多人的收益分配问题。本文研究的合作供能模式即是多主体参与的合作博弈问题,根据各个主体在合作项目中的贡献来对收益进行合理分配,即主体i 的收益等于i对其所参与联盟的边际贡献均值。
假设I={1,2,3,…,n}为n 个参与合作项目的主体集合,对于I 的任一子集S∈I,均对应一个实数函数F(S),该函数满足:
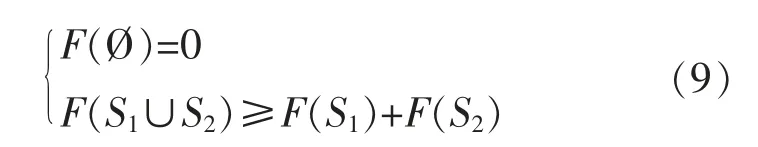
式中:F(S)为联盟S 的合作收益,即使联盟人数增加,其收益也不会减少。联盟内主体i 的利益分配所得值为
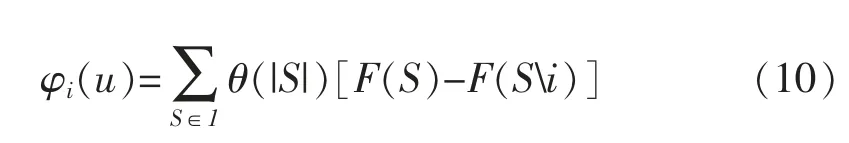
式中:S 为包含成员i 的所有子联盟;|S|为子联盟S中成员的个数;F(S\i)为子联盟S 除去成员i 后的收益;F(S)-F(S\i)为成员i 对子联盟S 的边际贡献;θ(|S|)为联盟S 出现的概率,计算公式为

园区分布式综合能源系统中由多个主体进行合作时,根据理性原则,合作收益应不小于各主体单独供能时的各主体收益之和。园区主体通过合作联盟增加的收益包含两部分:联盟参与者增加投资所产生的收益和联盟内部对于所掌控资源的合理配置所产生的协作收益,两者合称增量收益,可由式(12)表示。基于此,应用Shapley 值法对增量收益进行分配。

3 算例分析
3.1 园区基本情况
以某工业园区为研究对象,园区位于我国北方区域,存在冬季供暖负荷,供暖季为国家法定121 天,供暖建筑面积为10 万m2,选取冬季典型日的园区电热负荷曲线作为基础数据,如图3 所示,典型日时长取24 h。园区内主体主要包括分布式光伏运营商、热电联产运营商以及用户三大主体。分布式光伏出力特性曲线如图4 所示,其他边界计算条件分别为:光伏全额上网电价0.65 元/kWh,光伏余额上网补贴电价为0.32 元/kWh,光伏直供电价为0.7 元/kWh。园区热电联产机组采用人马座40 型号的机组,燃机出力为3 418 kW,热电比为164.59%,天然气消耗量为1 280 m3/h,当地的天然气价为2.31 元/m3。园区储能装置暂未投入使用。用户从市政购热价格实行两部制热价,基础热价为18 元/m2,计量热价为0.25元/kWh,用户从热电联产直购热价为91 元/GJ,从电网购电的分时电价如表1 所示,从热电联产购电的直供电价如表2 所示。
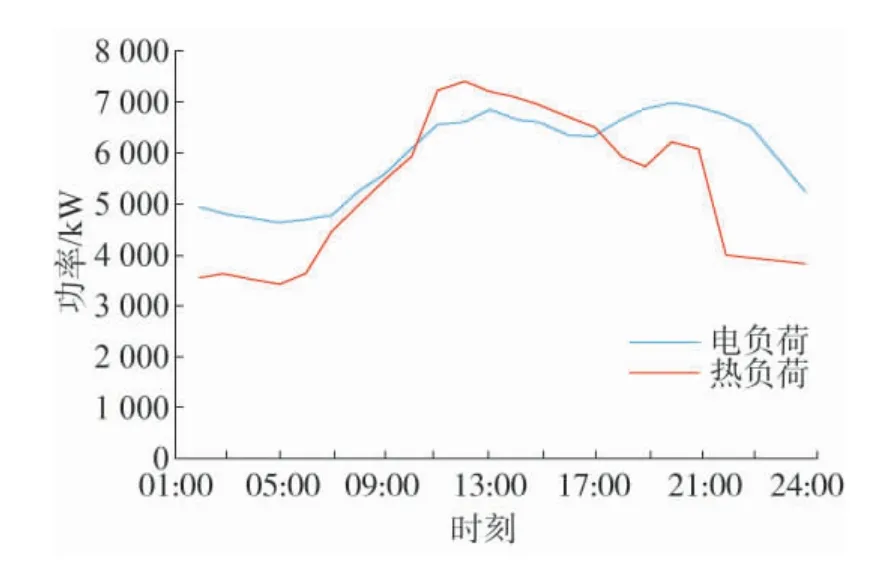
图3 冬季典型日园区负荷曲线
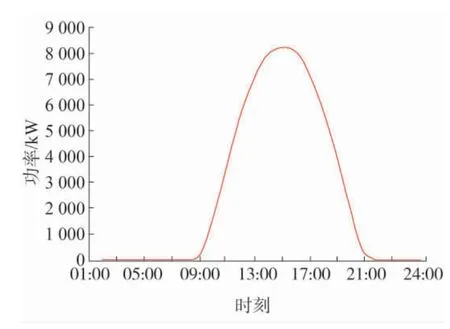
图4 冬季典型日园区光伏出力特性曲线
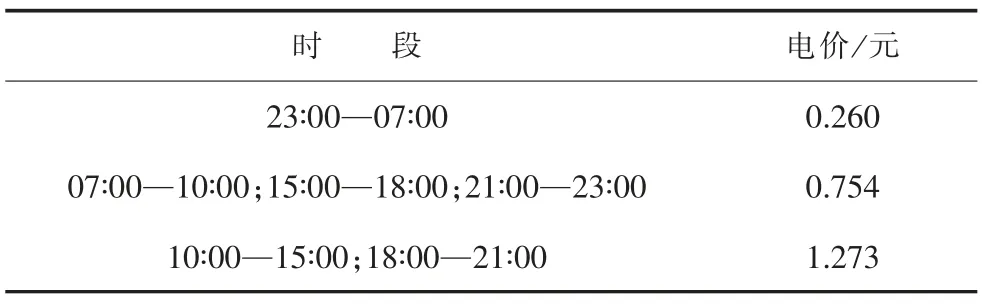
表1 电网购电分时电价
应用构建的园区各主体收益模型,分别测算园区独立运营模式以及合作运营模式下的总体收益可得,独立模式系统总体收益为-9.943 8 万元,合作运营模式下总体收益为-5.889 3 万元,两种模式相比,其增量收益为4.054 5 万元。由于用户用能需求量以及系统内的能源供应量均不会随着模式转换而改变,增量收益主要来源于在因合作运营模式下对系统内能源的合理调度。两种模式下总收益为负是因为系统内电能和热能供应不足,需要从外部电网、热网获取能源。

表2 热电联产直供电价
3.2 增量收益分配
将园区内3 个主体通过合作运营创造出来的增量收益作为分配的总收益,直接应用Shapley 值法可得各种在主体的分配结果,分别如表3—表5 所示。
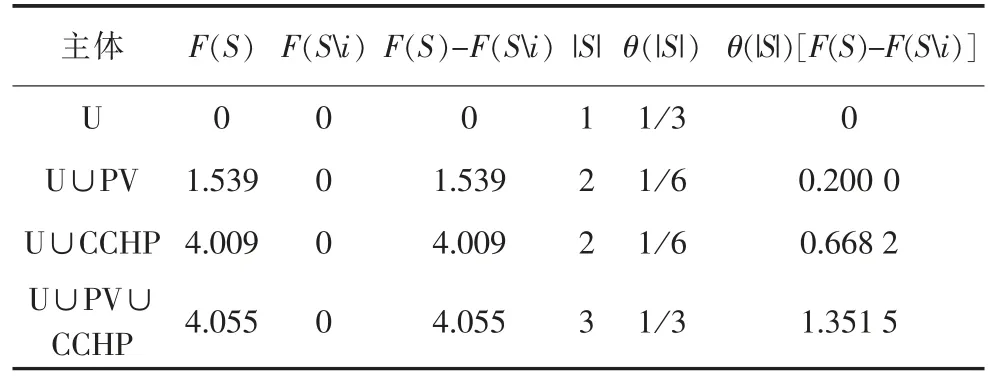
表3 用户收益分配
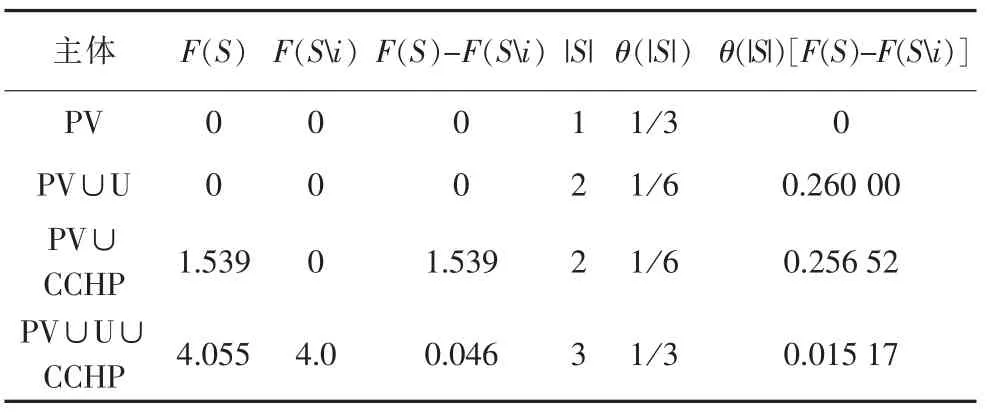
表4 分布式光伏收益分配
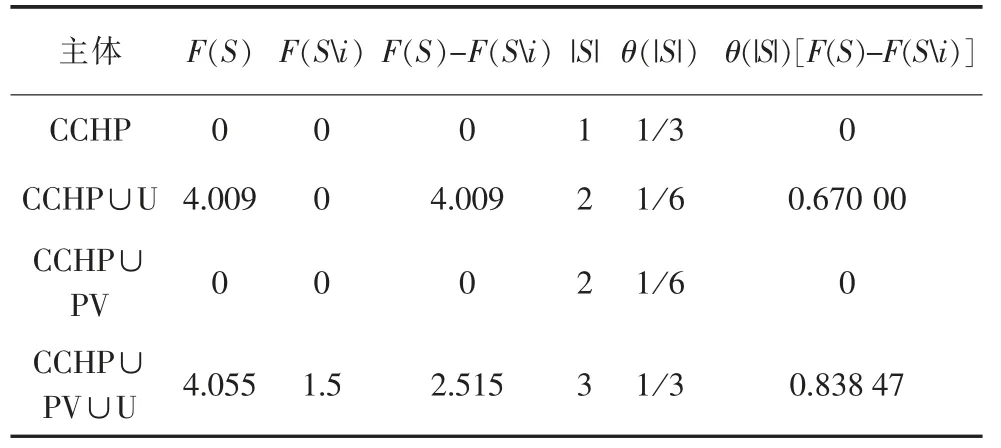
表5 热电联产收益分配
将表3 中最后一列数字相加得到园区内用户应分配的增量收益φU(u)=2.276 2 万元,同理,可得园区内光伏运营商应分配的增量收益为φPV(u)=0.271 7 万元,园区热电联产运营商的收益为φCCHP(u)=1.506 6 万元。从计算结果可以看出,合作模式下用户的用电用热成本降低,其余主体的收入均有所增加;因此系统内各主体直接进行电量和热的交易有益于降低运行成本,提高收益。合作供能模式中,用户用能成本降低2.276 2 万元,光伏系统增加收益0.271 7 万元,热电联产增加收益1.506 6 万元。因此园区分布式综合能源系统更适合采用合作供能运营。
4 结语
针对分布式综合能源的特点,得出园区内多个主体参与下的2 种运营模式,即独立供能模式和合作供能模式;通过对2 种模式下不同主体的行为分析,建立各主体收益函数和总体增量收益函数;应用Shapley 值法对增量收益进行分配。计算结果表明,园区内多主体进行合作联盟,在合作供能模式下能增加整个系统的总体收益,有效应用提升整个系统的经济效益,Shapley 值可以较为公正合理的对增量收益进行分配,有利于加强合作联盟的整体协作,保障园区分布式综合能源系统创造的社会效益。

