随机需求下双渠道供应链库存动态交互优化

赵 川，苗丽叶*，杨浩雄，何明珂

（1.北京工商大学商学院，北京 100048；2.北京物资学院物流学院，北京 101100）

0 引言

随着互联网应用的普及与电子商务的发展，越来越多的企业采用传统线下分销式零售与线上网络式直销相结合的双渠道运营方式，双渠道供应链分别指由厂家直销的线上购买渠道和通过门店、实体店等进行产品销售的线下渠道。现有文献关于双渠道供应链的研究主要集中在定价策略、渠道间的竞争与合作以及渠道选择、博弈和协调等方面，而随机需求下的双渠道库存策略和库存控制是近年来兴起的研究重点之一，有少部分文献考虑了双渠道研究中的库存优化，但并未将控制理论应用其中，也鲜有文献考虑库存控制的时效性和交互性。针对渠道间补货的交互性和动态性，本文以反馈控制理论为基本指导思想，通过将动态微分方程转化为控制模型的方式描述交叉补货的动态过程，考虑到双渠道交叉补货过程中周期间的交互性，上下游供应链成员间的交互性，以及线上线下渠道间的交互性，构造了双输入、双输出、多状态的复杂交互系统，利用延迟控制、反馈控制和比例-积分-微分（Proportion-Integral-Derivative，PID）控制，提出了一种随机需求下双渠道库存的动态交互优化模型，使库存系统达到缺货次数最少，缺货量最低的动态稳定状态。通过分别考虑双渠道在相同需求分布和双渠道不同需求分布情形下，单独控制、集中控制和交叉补货控制三种模式下的动态库存优化问题，对比双渠道供应链的最优决策策略。

1 相关工作

本文从双渠道库存优化和基于控制理论的库存优化两方面分别进行回顾和述评。

传统零售和网络直销并存的双渠道供应链是当今企业运营模式的新特点，针对这种新模式的库存控制方法，可使企业在激烈的市场竞争中占据优势地位，因此双渠道供应链库存控制已成为学术界研究的重点。文献［1］中提出了一个基于MTS生产方式的制造商和一个销售多种物品的零售商构成的两层供应链，研究了由制造商原材料、产成品和零售商商品构成的三层库存系统的多物品生产和补货问题。文献［2］中分析研究了双渠道是如何控制库存成本的，制造商利用传统渠道和直接渠道运送货物，采用马尔可夫链模型来制定总成本绩效，并根据泊松过程对库存进行补货。文献［3］中研究了集中式决策和基于Stackelberg博弈这两种情况下的双渠道供应链的定价、服务及库存需求的关系。文献［4］中针对由仓库和多个零售商组成的二级供应链问题，考虑仓库面临零售商和网络销售两种渠道以及不同零售商的优先级不同的情况，建立解析模型。以最小化供应链总成本为目标，设计了一种改进型遗传算法，并提出了一种两阶段分配策略求解模型。文献［5］中研究了在需求扰动的情况下，由传统渠道和在线渠道组成的系统库存控制策略问题。参考固定需求下的双渠道独立库存模型，建立了需求扰动下的双渠道独立和联合两种库存控制模型。文献［6］中考虑了由多个供应商、一个配送中心组成的二级供应链系统在市场需求为随机情况下的多品种库存问题，建立了一个混合整数非线性规划模型，利用求解多元函数条件极值的办法来求解该问题模型。文献［7］中考虑了供应链中传统线下渠道和线上渠道的定价决策问题。在此基础上，利用三种不确定规划模型推导出渠道成员在三种权力结构下的定价决策。文献［8］中提出一种在线渠道价格折扣和线下渠道价格折扣契约来协调供应链库存决策。以上文献都主要是从数理统计方面研究双渠道库存控制问题，而鲜有文章从动态供需平衡的角度讨论库存，也没有文章考虑生产延迟和物流延迟。众所周知，现实生活中的库存问题相关因素甚是复杂，只有充分考虑相关因素，才能深层次地研究库存问题。

另一方面，随着控制理论在经济、管理领域的发展，一些学者开始将控制理论应用于库存管理的研究中。首次将控制系统思想应用于库存控制的是美国学者Herbert A.Simon。文献［9］中将库存优化问题看作一个控制系统，并且应用拉普拉斯变换将微分方程转换成控制系统的传递函数。文献［10］中针对闭环供应链中的库存优化和牛鞭效应等问题，通过对单级库存系统的传递函数进行Z 变换后，利用遗传算法经过参数整定对闭环库存PID控制后发现，PID控制器能够有效降低库存和系统的牛鞭效应。文献［11］中通过建立库存系统的状态空间方程，利用极点配置状态反馈的方式构建了库存控制系统，并通过实证研究证明了该系统的可行性与有效性。文献［12］中在顾客到达时间间隔、回收品到达时间间隔、制造和再制造过程都服从不同参数的指数分布时，建立了无限期折扣总成本准则下的马尔可夫决策模型，并通过系统的最优方程，分析得到了最优策略的结构解析性质。文献［13］模拟了一个切换时变延迟系统，研究了具有马尔可夫跳跃参数和时变时滞的两时间尺度生产库存系统的H∞控制，基于Lyapunov-Krasovskii 理论，给出了足够的条件，使得两个时间尺度的生产库存系统通过有效地减弱牛鞭效应而呈指数稳定。文献［14］中运用仿真优化技术，基于离散事件系统仿真原理，建立了随机性（Q，r）库存系统的仿真模型，设计了一种改进的遗传算法并应用它优化库存系统的库存控制策略。文献［15］中基于随机动态优化理论和自抗扰控制两种不同方法，对比研究经典的随机生产库存模型。文献［16］中构建了一个由第三方逆向物流企业回收废弃产品模式下的闭环供应链混合库存动态模型，并应用鲁棒控制和线性矩阵不等式算法对闭环供应链系统的动态性能进行研究。以上文献都主要从经典的输出反馈控制、PID 控制以及现代控制理论的角度研究了确定型需求和随机型需求的库存系统优化问题，但还鲜有文章利用控制理论研究双渠道库存动态交互优化问题。

由于渠道间的补货过程具有动态性和交互性，即上一周期的库存经过订货、交货和运输延迟到达下一周期时，并不是静态的进销存计算过程；且上一周期的剩余库存需反馈回到下一周期的进销存过程中，以此指导下一周期的订货。因此，交叉补货的周期变化不仅影响到线上线下间的进销存系统，也影响到上下游间的进销存系统，还会影响到前后周期乃至全周期的进销存系统，是一个复杂动态的交互变化过程。再者，双渠道库存的大幅度动态变化极易造成大量缺货或库存积压、资金链断裂等情况，因而保持库存系统持有量低且稳定是极为重要的，这也是本文要解决重点的问题。

本文针对以上两类文献研究的不足，综合考虑现代库存研究的相关因素，结合控制理论和库存优化，并根据线上线下不同销售渠道的特点，基于反馈控制理论，首次刻画了双渠道单独控制、双渠道集中控制和双渠道交叉补货控制三种模式下的库存动态控制系统，构造了多个双输入、双输出的复杂（交互）系统。通过仿真模拟渠道间动态补货、反馈指导订货过程，并利用延迟控制、反馈控制和PID 控制优化库存系统，通过Simulink 中的一系列控制模块，优化了双渠道库存系统每一周期的订货、运输延迟、交货、交叉补货的动态过程。

2 问题描述与基本假设

在一个随机需求下的线上线下双渠道供应链系统中，首先考虑线上线下不同分布的情况，可参考文献［17-18］，即假设线上需求函数服从均匀分布，线下需求函数服从正态分布。在动态库存系统优化的研究中，生产延迟、物流延迟等构成的交货延迟是影响库存管理的重要因素，延迟越大，提前期越长，不确定因素越多，导致缺货与积压等库存系统的不稳定。本文采用“订至点”订货策略，即首先根据上期实际销售情况预测本期期望库存，进而与现有库存进行对比决定是否进货。本文基本符号设计如表1所示。

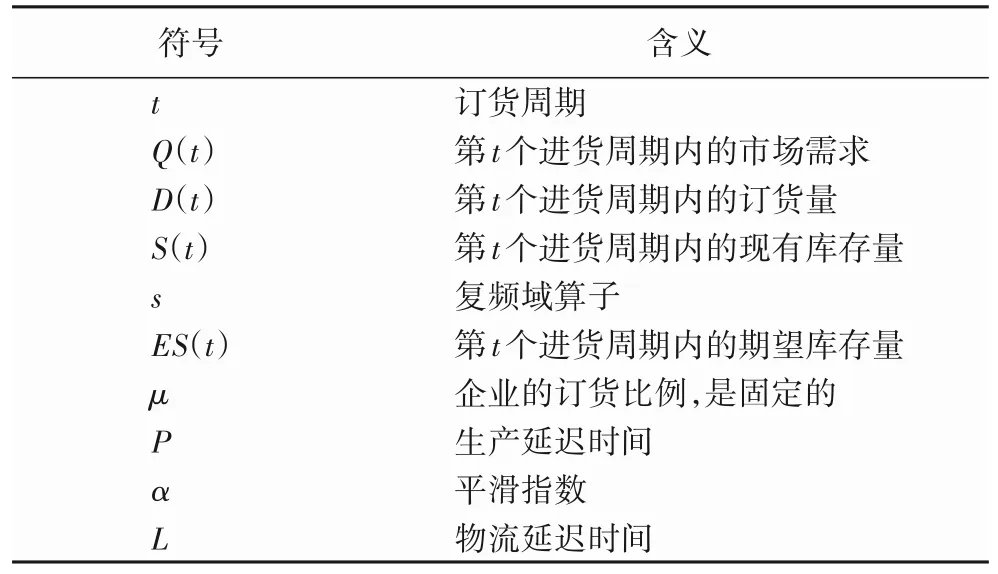
表1 基本符号设计Tab.1 Basic symbol design

现作出以下假设：

1）只考虑单级供应链库存系统，即一个供应商和一个零售商。

2）存在生产延迟。即当企业向上级供应商发出订单后，上级供应商经过一定时间结束现在的生产任务后才会展开对新的订单的生产任务。

3）存在物流延迟。即当上级供应商收到订单后，需要一定的运输时间。

4）市场需求是随机的，即Q(t)=x，x为随机数。

5）渠道间存在交叉补货，即存在物流延迟。

6）物流延迟0＜P＜1，生产延迟0＜L＜1，且0＜P+L＜1，即物流延迟和生产延迟之和小于一个生产周期。

3 模型建立

零售企业在一个进货周期t中，向供应链上游企业订货并收到货物进而形成库存s（t），通过对货物进行销售消耗掉一部分库存，使随机市场需求Q（t）得到满足；至该销售周期期末，对现有库存量即剩余库存量进行盘点；根据本期实际销售情况预测下一期需求并制定期望库存水平ES（t）；通过比较本期剩余库存量和下期期望库存量得到库存偏差，根据库存偏差决定是否订货。根据订至点逻辑模型分别对基本库存控制、双渠道集中库存控制和双渠道交叉补货库存控制三种不同方式建模。

3.1 基本库存控制建模

按“订至点”补货策略订货，并考虑生产延迟和物流延迟，订货量为库存偏差的一定比例。

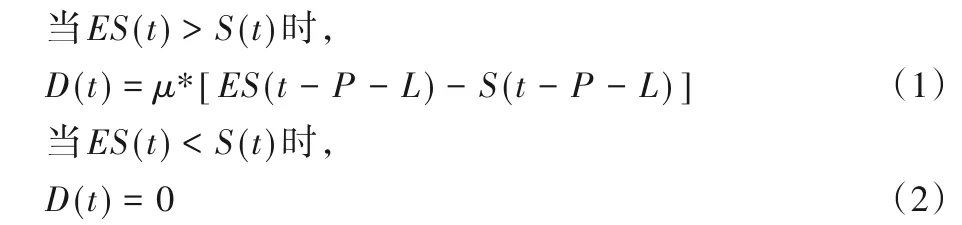
经过一个周期的销售，库存的变化量为该周期的订货量和市场需求之差。

当ES(t) ＞S(t)时，

3.2 集中库存控制建模

集中库存控制是指两个渠道分别销售，面对服从不同分布的随机市场需求，共用同一库存，但分别根据共用库存的状态制定订货策略。逻辑框图如图1所示。

图1 集中库存控制系统逻辑框图Fig.1 Logic diagram of centralized inventory control system

角标为1代表线下渠道，角标为2代表线上渠道。对于线下渠道：

利用指数平滑预测随机需求，可得到集中库存控制系统的闭环传递函数。

3.3 交叉补货库存控制建模

交叉补货库存控制是一个典型动态交互优化的过程，指的是两个渠道分别管理各自库存，但形成互相补货的同盟。以线下渠道缺货向线上渠道补货为例，当线上渠道缺货时，由于生产时间和物流时间较长的原因，不会向供应链上游申请补货，而会立即向坐落在附近的线下渠道仓库调货；线下渠道收到调货申请后会先满足自身市场需求，随后盘点剩余库存，若有剩余，则向其补货。若发生补货，货物不会经过生产延迟，只会经过少许运输时间到达线上渠道。线上渠道的需求得到全部或部分满足，此时线上渠道的剩余库存为零，并据此制定下一周期的订货策略，线下渠道也会根据补货后的剩余库存制定下一周期的策略。同周期只会发生单向交叉补货，当双渠道同时缺货时，不发生交叉补货。交叉补货库存控制基本逻辑流程如图2所示。

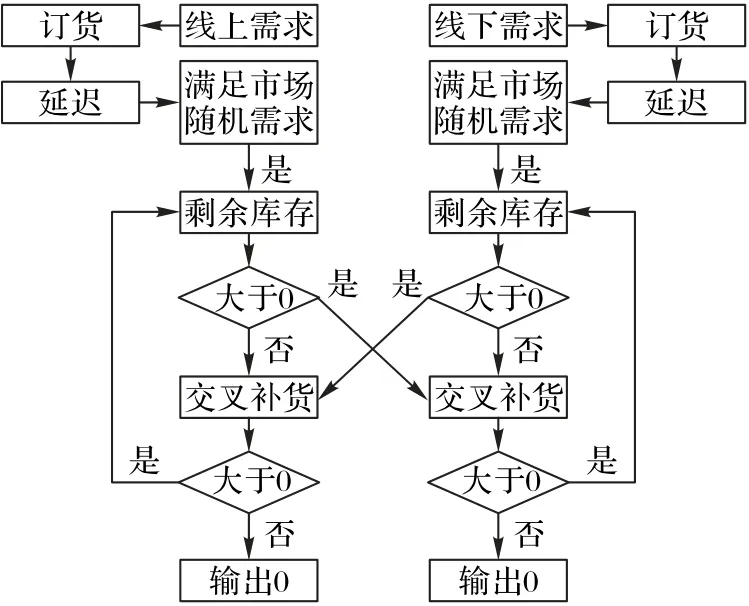
图2 交叉补货库存控制系统逻辑流程Fig.2 Logic flowchart of cross-replenishment inventory control system

角标为1代表线下渠道，角标为2代表线上渠道。经过一个周期的销售后，线下渠道剩余库存为：

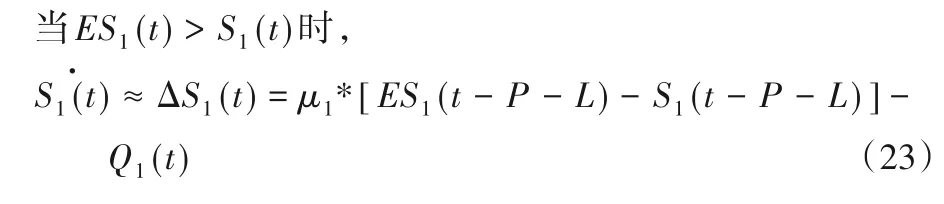
4 算例分析

为了达到更高的精度，采用将连续系统进行离散取样。当线上线下渠道为不同分布时，进行独立库存、集中库存和交叉补货库存控制仿真。

4.1 独立库存控制仿真

独立库存控制是指线上线下两个渠道分别控制库存，互相之间不进行沟通和调货补货。不失一般性，此处假设线上销售渠道的市场需求服从均匀分布，而线下销售渠道的需求服从正态分布，在SIMULINK仿真平台上建模并仿真。

1）线上渠道库存控制。

本文利用Matlab 随机生成一列300～800 的服从均匀分布的随机数列以模拟线上随机市场需求。根据调研，行业平均延迟时长为半个周期。据此，不失一般性，本文设定总交货延迟时间为0.5个周期，故生产延迟时间P和物流延迟时间L选取为0.2和0.3，订货比例µ设为1.6，平滑指数α设为0.5。对线上渠道库存系统的反馈控制模型进行仿真，仿真结果如图3所示。

图3 线上渠道的期望库存量和剩余库存量Fig.3 Expected stock and residual stock of online channel

结果显示，在这套参数下，库存系统受均匀分布的随机需求影响，在第5个进货周期达到稳态，从第6周期开始观测（下同），平均剩余库存为274，缺货6 次，分别是第11、19、30、31、37、49周期，但缺货幅度较小。

2）线下渠道库存控制。

本文利用Matlab 随机生成一列均值为600、方差为12 的服从正态分布的随机数列以模拟线下随机市场需求，生产延迟时间P和物流延迟时间L分别选取为0.2 和0.3，订货比例µ设为1.6，平滑指数α设为0.7。对线下渠道库存系统的反馈控制模型进行仿真，仿真结果如图4所示。

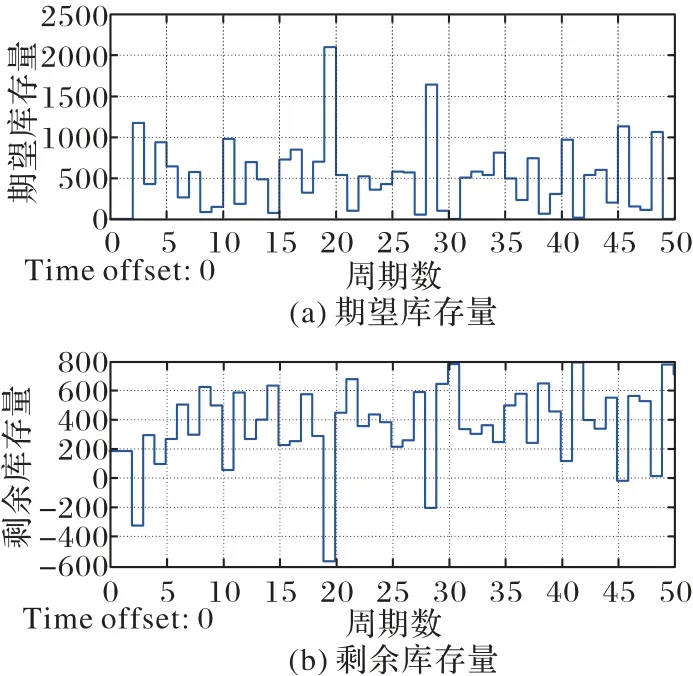
图4 线下渠道的期望库存量和剩余库存量Fig.4 Expected stock and residual stock of offline channel

结果显示，在这套参数下，库存系统受正态分布的随机需求影响，从第5个进货周期达到稳态，从第6周期开始观测，平均剩余库存为234，缺货6 次，分别是第10、19、28、40、45、48周期。图中可看到有明显的缺货，如第19 周期，究其原因，是因为在第19周期需求大幅增加，导致缺货量幅度较大。

4.2 集中库存控制仿真

集中库存控制是指线上、线下渠道分别面对市场需求进行进货决策，并将库存保存在同一仓库内集中控制。变量设置如表2 所示，对双渠道集中库存反馈控制系统进行仿真，SIMULINK仿真框图如图5所示。

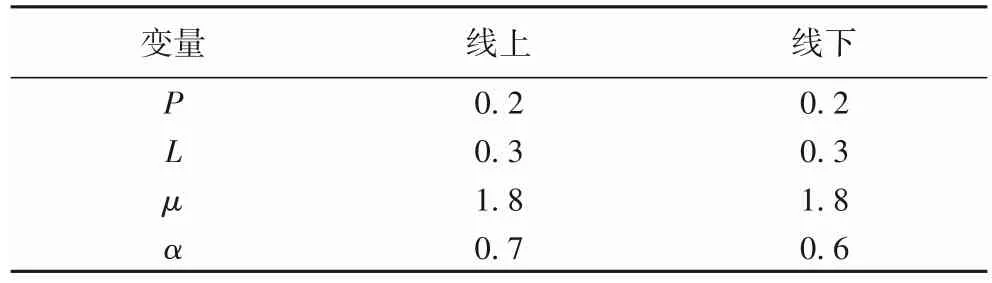
表2 集中库存控制变量设置Tab.2 Variable setting of centralized inventory control

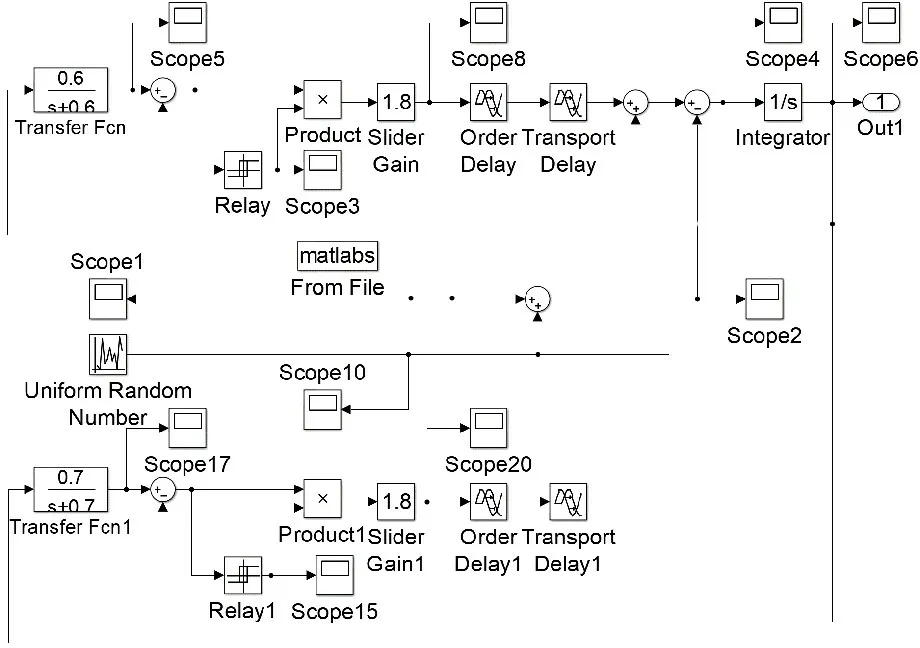
图5 随机需求下集中库存控制系统仿真框图Fig.5 Simulation block diagram of centralized control inventory system under stochastic demand

仿真结果如图6所示。结果显示，在这套参数下，线上、线下渠道共同的平均剩余库存为399，缺货次数为6次，分别是第21、28、37、39、46、48周期。此结果在同一参数同一缺货次数的条件下，比独立库存控制两个渠道相加的平均剩余库存要小。虽有6次缺货，但缺货幅度均不大，说明集中库存控制虽无法明显降低缺货次数，但在降低平均剩余库存方面效果显著。在此需说明，集中库存控制如果出现缺货，则是两渠道均缺货。

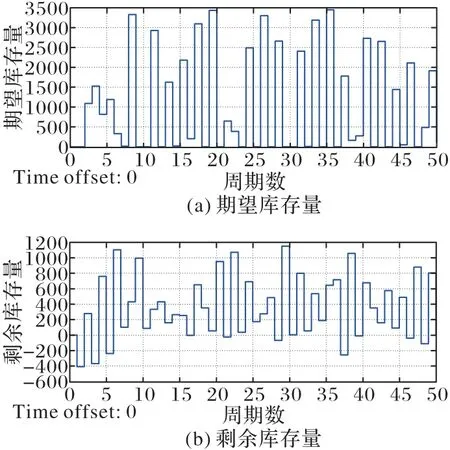
图6 集中控制下期望库存量与剩余库存量Fig.6 Expected stocks and residual stock under centralized control

4.3 交叉补货库存控制仿真

交叉补货库存控制是指，当其中一个渠道缺货，而另一个渠道库存有剩余时，由有剩余库存的渠道向有缺货的渠道进行临时补货，进而使两个渠道的库存得到充分利用，可以最大化销售所得利益，同时达到降低库存的目的。初始条件和参数设定与独立库存控制的设定一致，不同的是，此处增加了渠道间交叉补货的物流延迟，设定为0.1，变量设置如表3所示。对双渠道交叉补货库存控制模型进行仿真，SIMULINK 逻辑框图如图7所示，SIMULINK仿真框图如图8所示。

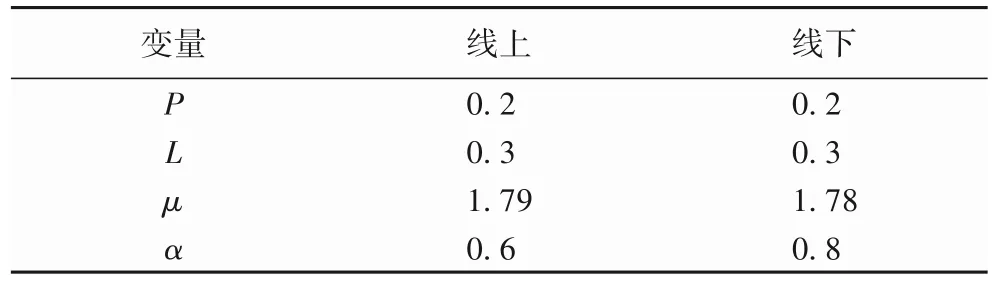
表3 交叉补货库存控制变量设置Tab.3 Variable setting of cross-replenishment inventory control

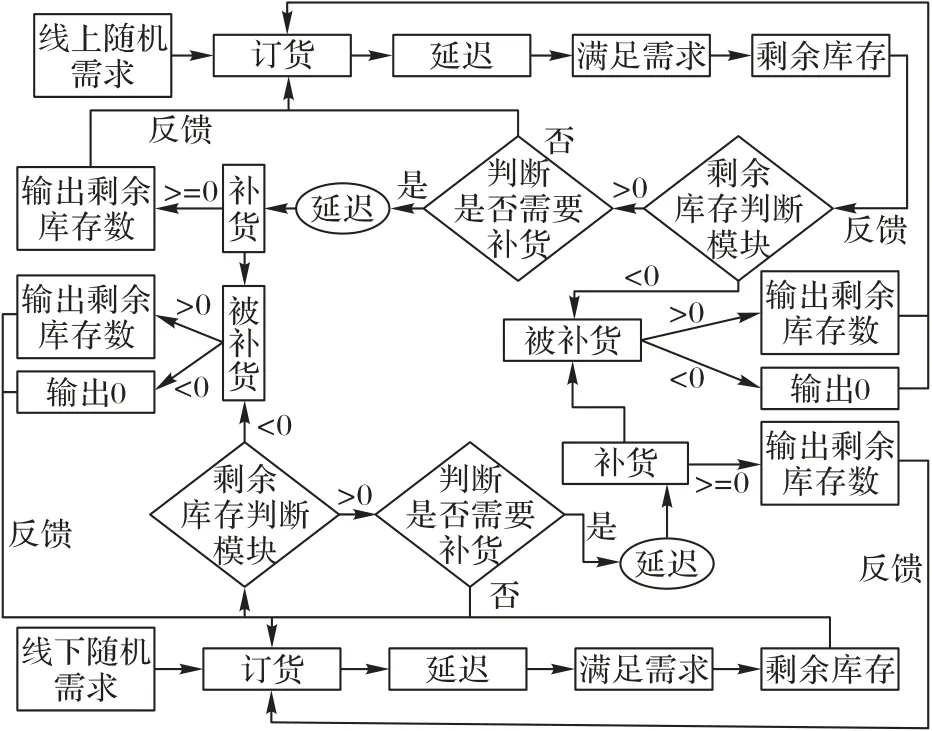
图7 交叉补货库存控制系统逻辑框图Fig.7 Logic diagram of cross-replenishment inventory control system

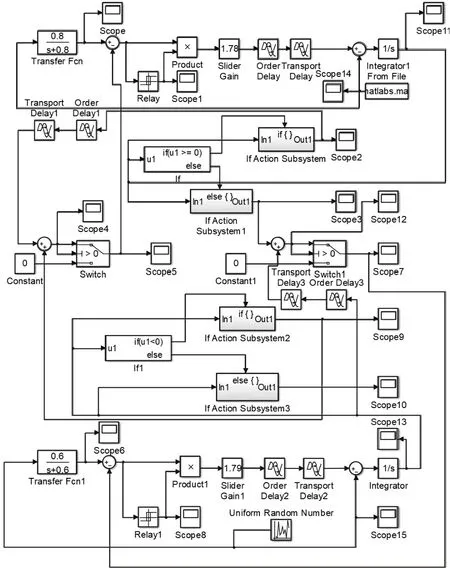
图8 随机需求下交叉补货库存控制系统仿真框图Fig.8 Simulation block diagram of cross-replenishment inventory control system under stochastic demand

仿真结果如图9 所示。结果显示，在这套参数下，线下渠道缺货次数为5 次，即需要补货的周期数为5 个，分别是第10、16、19、28、40 周期，平均剩余库存为231；线上渠道缺货次数为6 次，即需要补货的周期数为6 个，分别是第26、30、33、37、43、46 周期，平均剩余库存为279。接下来将进行交叉补货，交叉补货后，双渠道库存系统的仿真结果如图10所示。

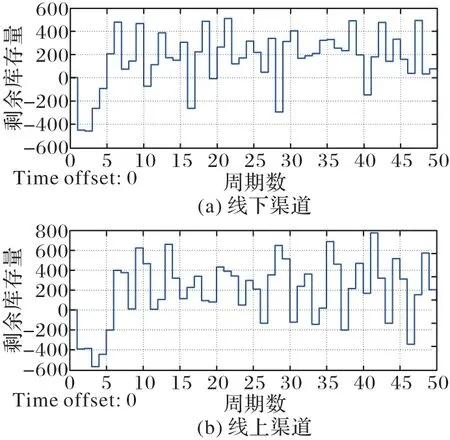
图9 交叉补货前线下线上渠道系统剩余库存量Fig.9 Residual stocks of offline and online channel system before cross-replenishment

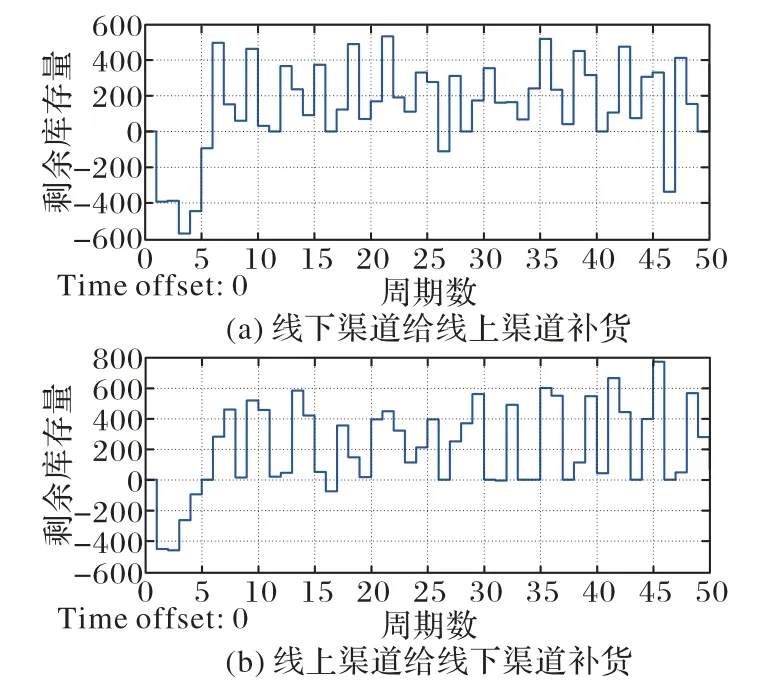
图10 交叉补货后线上线下渠道系统的剩余库存量Fig.10 Residual stocks of online and offline channel inventory system after cross-replenishment

由图10可知，线下渠道给线上渠道补足了4次货，分别补足了第30、33、37、43周期。其中：第30周期，线下渠道向线上渠道补货476 单位，补货后剩余库存353；第33 周期，补货211单位，补货后剩余库存66；第37 周期，补货242 单位，补货后剩余库存39；第43 周期，补货209 单位，补货后剩余库存74。补货完成后，线上渠道缺货从6 次下降到2 次，分别是第26、46周期，此时平均剩余库存为266。仿真结果见表4。

线上渠道给线下渠道补足了3次货，分别补足的是第10、19、40 周期。其中：第10 周期，线上渠道给线下渠道补货530单位，补货后剩余库存454；第19 周期，补货28 单位，补货后剩余库存18；第40 周期，补货192 单位，补货后剩余库存43。补货完成后线下渠道缺货2 次，分别是第16、28 周期，平均剩余库存为217。仿真结果见表5。

对仿真结果进行分析可得，当两个渠道发生交叉补货后，除个别周期会有少量缺货发生外，一般情况下交叉补货均可满足两个渠道的需求，说明交叉补货不仅可以满足双渠道不同的市场需求，获得利润，还可以降低两个渠道的库存成本，同时在减少紧急补货成本方面也有很大的优势。

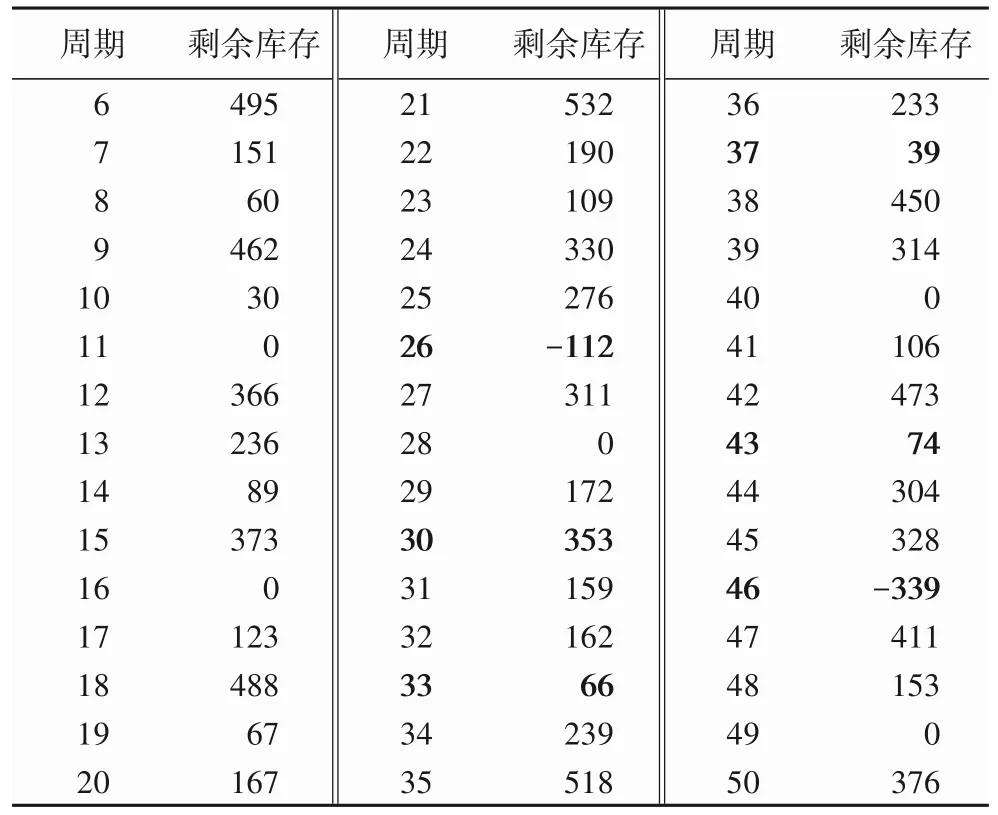
表4 线下给线上渠道补货后的反馈控制系统剩余库存量Tab.4 Residual stocks of feedback control system after offline channel replenishing online channel

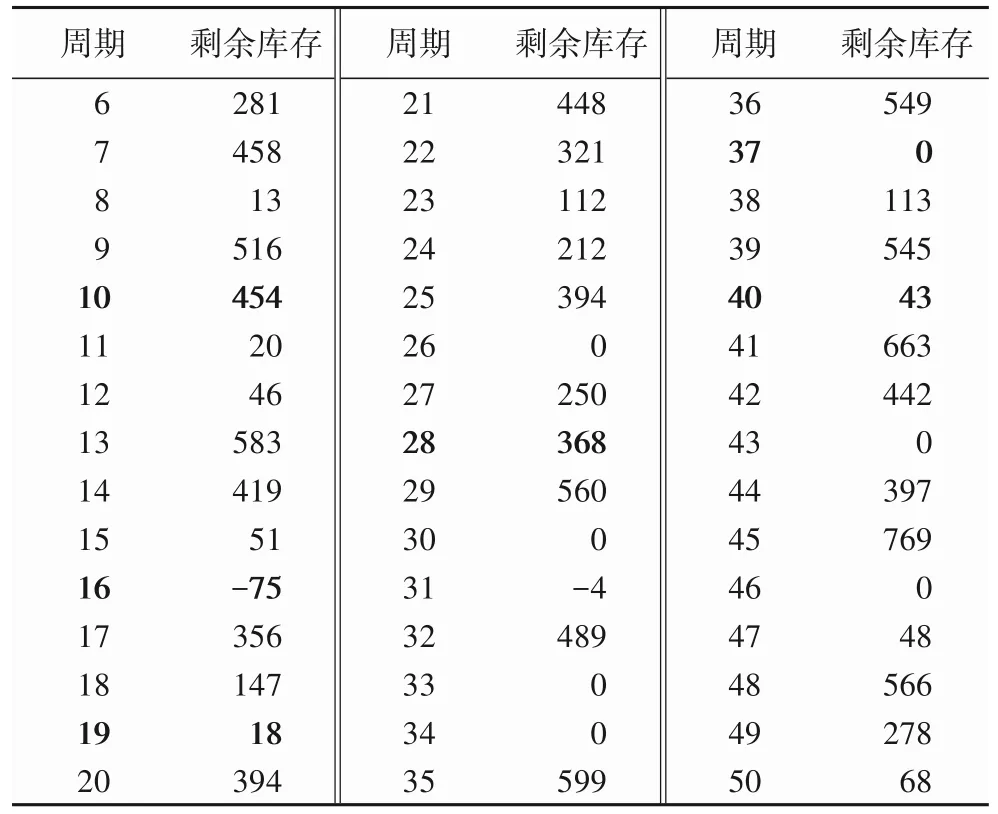
表5 线上给线下渠道补货后的反馈控制系统剩余库存量Tab.5 Residual stocks of feedback control system after online channel replenishing offline channel

为了更直观显示交叉补货的有效性，本文选取对应参数对双渠道独立库存控制、集中库存控制和交叉补货库存控制的库存情况做了同维度的对比研究，即保持平均库存一致，比较缺货次数，或反之。结果见表6所示。

根据对比结果分析可得：

1）随机需求下，集中库存控制优于独立库存控制。在缺货次数相同的情况下，集中库存控制平均剩余库存（399）比独立库存控制（274+234）少109 个单位，说明集中库存控制可以降低双渠道库存成本。

2）随机需求下，交叉补货库存控制优于独立库存控制。交叉补货库存控制的平均剩余库存（483）比独立库存控制（274+234）少25 个单位，且缺货次数大幅减少，说明交叉补货库存控制可以大幅降低双渠道缺货成本。

3）随机需求下，交叉补货库存控制优于集中库存控制。为了便于将交叉补货库存和集中库存相比较，本文将集中库存控制的平均剩余库存调整到了483。故在平均剩余库存相等的情况下（483），交叉补货的缺货次数远低于集中库存控制，说明交叉补货库存控制可以有效降低双渠道缺货成本。

表6 不同分布下三种情况平均剩余库存及缺货次数对比Tab.6 Comparison of average residual stock and out-of-stock times in three conditions under different distributions

为考虑实验完整性，本文在相同背景下假设线上线下渠道为同种分布，得到如表7结果。

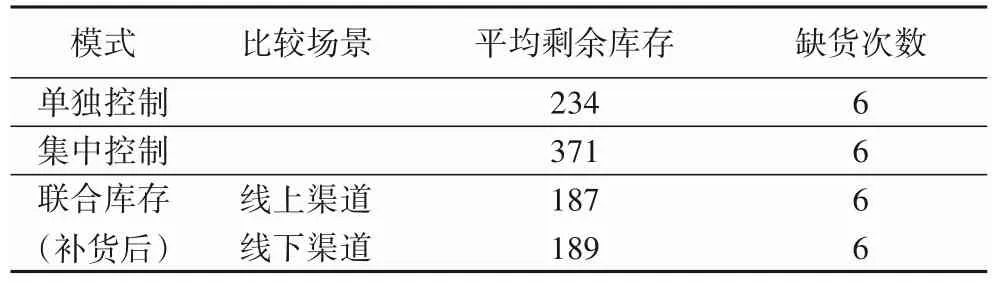
表7 同种分布下三种情况平均剩余库存及缺货次数对比Tab.7 Comparison of average residual stock and out-of-stock times in three conditions under the same distribution

由表7 可得，当线上线下渠道为同种分布时，与不同分布的结论有所不同。

1）随机需求下，集中库存控制优于独立库存控制。在缺货次数相同的情况下，集中库存控制平均剩余库存（371）比独立库存控制（234+234）少97 个单位。因为集中控制相较独立库存来说，库存集中，在应对需求波动较大时有优势。

2）随机需求下，交叉补货库存控制优于独立库存控制。交叉补货库存控制的平均剩余库存（376）比独立库存控制（468）少92 个单位，且缺货次数大幅减少。因为交叉补货重在相互之间的补货，可以动态地调节库存，相较独立库存，在减少缺货次数和剩余库存方面都有显著改善。

3）随机需求下，集中库存控制略优于交叉补货库存控制。集中库存控制的平均剩余库存（371）比交叉补货库存控制（187+189）少5 个单位。在线上线下渠道为同种分布时，面临市场需求差别不大，上下渠道同时有剩余库存或产生缺货的概率较大，故交叉补货并不能发挥其优势，致使交叉补货策略在减少剩余库存方面和集中控制差别不大。

5 结语

从供应链管理的角度来看，将控制理论与库存模型相结合，可以为企业的库存优化提供参考。随着市场竞争的日益激烈，缺货已经成为库存成本增加的重要因素，在满足市场需求的同时降低补货运营成本成为了企业迫切需要解决的问题。随着双渠道经营方式的广泛应用，渠道间补货的经营方式也应运而生，如何协调和提高渠道间补货的效率也显得尤为重要，本文的主要工作就在于利用交叉补货策略动态优化双渠道供应链库存系统。本文的难点在于，通过控制理论将动态微分方程转化为控制模型以此描述交叉补货的动态过程，并通过调整Simulink仿真参数模拟渠道间动态补货、反馈指导订货的过程，使双输入双输出的复杂交互库存系统达到稳定状态。因此，本文综合利用延迟控制、反馈控制和PID控制优化了周期间、上下游间、双渠道间的订货、运输、交货、交叉补货的全过程。

综上，通过Simulink 仿真研究，双渠道库存系统可以达到交叉补货中的供需动态平衡，并可以使补货过程中的库存系统保持稳定状态。通过数值仿真实验，对比三种双渠道库存控制策略得出，在线上线下渠道为不同分布的随机需求时，使用双渠道交叉补货策略能很好地降低剩余库存，从而为企业优化库存运营提供策略，为企业的实际生产运营提供理论借鉴。

对于双渠道供应链的企业，充分利用渠道间信用优势，加快双渠道间物流和库存的动态交互，相辅相成，节约成本节约时间，最大化系统获利，从而实现共赢。依托本文可进一步从多个方面进行拓展研究。本文只考虑了双渠道供应链库存系统，未来可针对多渠道混合供应链库存系统进行研究；另外，在未来的研究中，可以考虑按比例交叉补货的方式，降低双渠道交叉补货对自身系统的冲击。