铁路客运量预测模型对比分析

王雷，金勇，刘岩

1.大连交通大学 交通运输工程学院，辽宁 大连 116028；2.大连市国土空间规划设计有限公司，辽宁 大连 116000

0 引言

科学准确的预测铁路客运量是铁路规划的前提和基础，其目的在于获取规划区域内客流的特征和规律、交通基础设施的建设现状，为规划设计提供全面、系统、真实、可靠的参考资料和基础数据［1］，为铁路建设规划、项目投资和运营提供决策依据。

近年来，许多学者开始使用混合智能算法预测客运量。梁小珍等［2］针对时间序列包含噪声、单一模型预测不稳定的问题，提出了基于奇异谱分析的集成预测模型，并应用于我国年度航空客运量的预测中。李万等［3］提出改进粒子群算法，建立粒子群算法与长短时记忆神经网络相结合的预测铁路客运量的模型。纪鸿濛［4］比较微观和宏观预测领域不同模型的实用性和优缺点，提出了适用于高速铁路客运量预测的中观重力模型。鲜敏［5］在灰色系统理论和前反馈（back propagation，BP）神经网络原理的基础上构建预测模型，可较好地预测非线性铁路客运量。齐杉等［6］运用系统动力学方法分析铁路客运量的影响因素，运用多元回归预测理论，建立中长期预测模型。吴华隐［7］在分析铁路客运量影响因素的基础上，构建基于无偏灰色残差理论的铁路客运量预测模型，并以此预测未来5 a的客运量。褚鹏宇等［8］针对短期铁路客运量的特点，提出一种基于灰色理论的变权重组合预测模型。孙丽等［9］在考虑灰色特性和多重相关影响因素的基础上，运用偏最小二乘回归模型和灰色预测模型（grey prediction model，GM）（1，1）预测我国高速铁路客运量。袁胜强［10］通过分析灰色预测模型和BP神经网络模型的优缺点，最终采用马尔科夫链模型优化灰色BP神经网络模型的组合模型预测甘肃省铁路客运量。贺晓霞等［11］基于GM-周期扩展组合模型预测铁路客运量，充分考虑铁路客运量的周期性波动特征。陶海龙等［12］针对BP神经网络模型的缺点，提出基于粒子群优化算法优化BP神经网络参数，以此预测我国铁路客运量。Roos等［13］提出一种预测巴黎城市铁路网短期客流的方法，该方法基于动态贝叶斯网络，即使在数据不完整的情况下也可以预测。Glisovic等［14-15］比较了参数法和非参数法2种方法，提出基于遗传算法和人工神经网络集成的混合模型，用于预测塞尔维亚铁路的月客运量。Prakaulya等［16］分析时间序列成分，将时间序列分解模型应用于铁路乘客历史数据分析中。

综上所述，学者大多以年统计数据为基础，忽略了客运量周期性和趋势性的特点。本文在分析客流历史数据变化的基础上，采用季节性指数平滑法和季节差分自回归移动平均法（seasonal autoregressive integrated moving average，SARIMA）分别预测我国的铁路客运量，对比判断两种方法的短期预测精度，为铁路运输部门制定短期规划提供较为准确的参考依据。

1 客流预测模型

1.1 季节性指数平滑法

在20世纪60年代，温特斯（Winters）提出一种具有趋势变动和季节变动的时间序列方法，即季节性指数平滑法，它是指数平滑法中的一种高级形式［17］。考虑数据的季节性和趋势性因素，平滑不规则变动，修正线性趋势，处理季节性变动因素，扩大了指数平滑法的应用范围。其模型函数为：

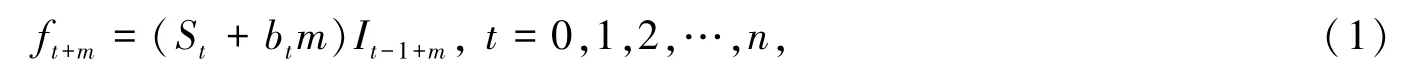
式中：St为平稳性函数，t为时间序列中的时刻；bt为趋势性函数，bt=γ（St-St-1）+（1-γ）bt-1；It为季节性函数为参数，取值区间为［0，1］；xt为历史时间序列；m为预测时刻距离现在时刻的时间间隔数；L为周期长度，如以月份为单位，L=12。

1.2 SARIMA模型

SARIMA模型是一种自回归差分移动平均（autoregressive integrated moving averagemodel，ARIMA）模型，该模型包含自回归模型（autoregressivemodel，AR）与滑动平均模型（moving average model，MA），是一种时间序列预测分析方法，可预测季节周期性数据［18-20］。

我国铁路月度客运量呈整体上升趋势，通过差分使其平稳化［21］。对铁路月度客运量建立随机变量｛Yt，t=0，1，2，…，n｝，满足

式中：φ（B）为 p阶自回归系数多项式，φ（B）=1-φ1B-φ2B2-…-φPBP，φ1，φ2，…，φP为自回归系数；B为延迟算子；θ（B）为 q阶移动平均系数多项式，θ（B）=1-θ1B-θ2B2-…-θqBq，θ1，θ2，…，θq为移动平均系数；εt为白色噪音，服从正态分布，其均值为0，方差为常数；d为原始序列平稳化时的差分阶数；p和q分别表示自回归阶数和移动平均阶数，BYt=Yt-1。

铁路客运量有较强的季节性，需在 ARIMA模型上增加季节差分，即 SARIMA（p，d，q）（P，D，Q）s（s为季节周期）模型，设时间序列｛Yt｝的周期为T，对于D阶季节差分有

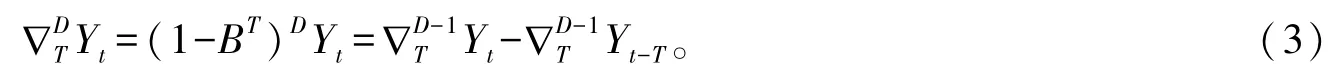
若存在d和D使｛Yt｝满足

则称｛Yt｝是季节周期为 s的 SARIMA模型（p，d，q）×（P，D，Q）s。 其中

式中：Φ（B）为回归系数多项式，Θ（B）为移动平均系数多项式，P为季节性的自回归阶数，Q为移动平均阶数。

2 铁路客运量预测

随着国民经济的增长以及近年来高铁的建设和开通，同时受国家法定节假日及学生寒暑假的影响，铁路客运量整体呈现增长趋势并且具有一定的周期性［22］。国家统计局2005年1月至2018年12月的铁路客运数据如图1所示。

2.1 指数平滑法预测

2.1.1 模型选择

季节性指数平滑法模型有简单季节性、温特斯加性、温特斯乘性等多种类型。分别用这3种模型预测，以2005年1月至2018年12月铁路客运量为训练集，以2019年每月的客运量为测试数据，得到季节性温特斯乘性模型效果最好，结果显示：温特斯乘性指数平滑法模型的均方根误差（rootmean square error，RMSE）、平均绝对百分比误差（rootmean square error，MAPE）及正态化贝叶斯信息准则（bayesian information criterion，BIC）分别是 1 035.362、4.136、13.977；可决系数R2=0.97，说明总变异中可以用温特斯乘法解释的部分占97%。

2.1.2 模型预测

用温特斯乘性模型对2005年1月至2018年12月铁路客运量进行拟合，拟合曲线见图1。利用温特斯乘性模型预测2019年1月至12月的铁路客运量，结果见表1所示，预测结果均在95%的置信区间内。

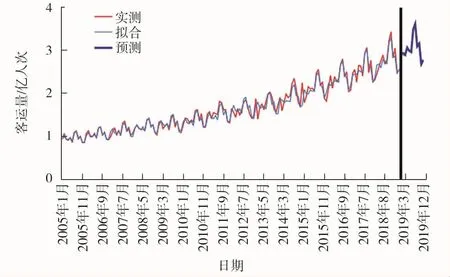
图1 温特斯乘性模型预测曲线

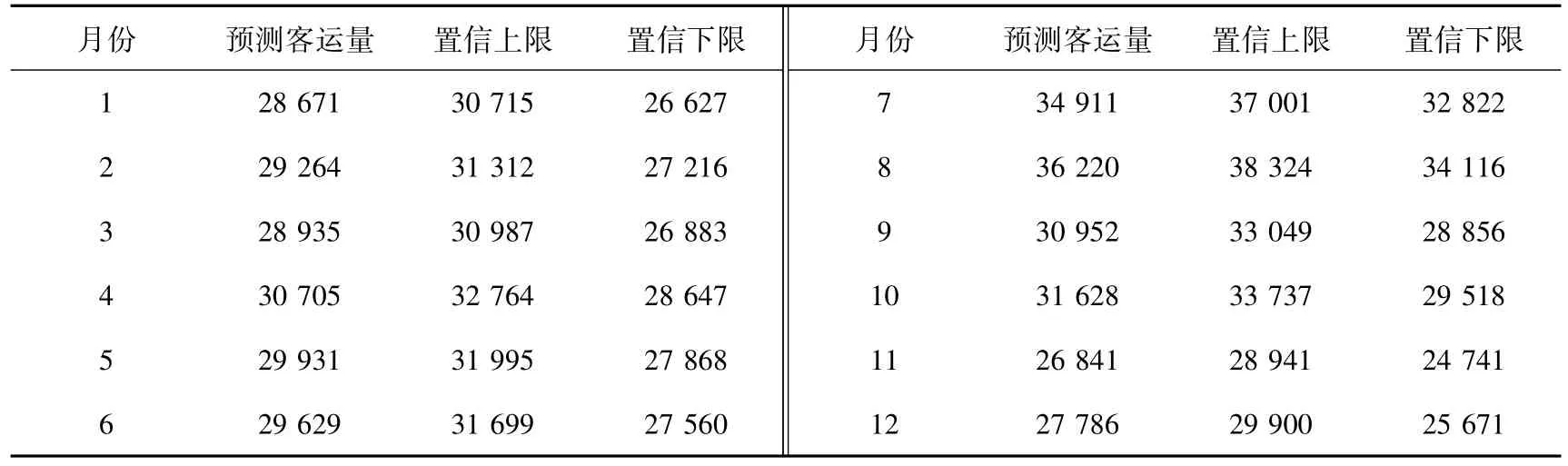
表1 2019年铁路客运量温特斯乘性模型预测结果 万人次

2.2 SARIMA模型预测

2.2.1 数据平稳化与预处理

根据图1初步判定数据不平稳且带有明显的周期特征，为了更准确地判断，对其进行单位根检验（augmented dickeyfuller，ADF），计算t-统计和概率，结果如表2所示。由表2可知，检验统计量（test statistic）为0.961 794，大于不同水平下的t-统计。说明接受序列有一个单位根的原假设，检验结果为未通过，表明2005年1月至2018年12月的客运量序列存在单位根，是非平稳序列，需要进行差分处理。又因其具有明显的季节规律性，对其进行一阶季节差分处理。差分处理后得到时序图，如图2所示。由图2可以看出曲线没有明显的周期性和增长趋势，可初步判断实现了时间序列的平稳化。

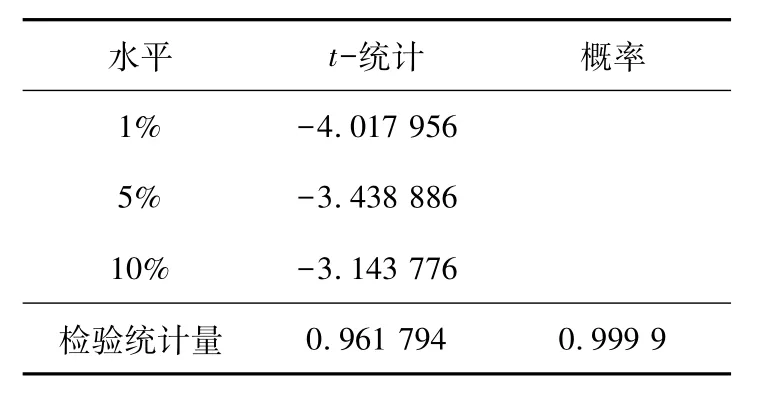
表2 原始序列ADF检验结果

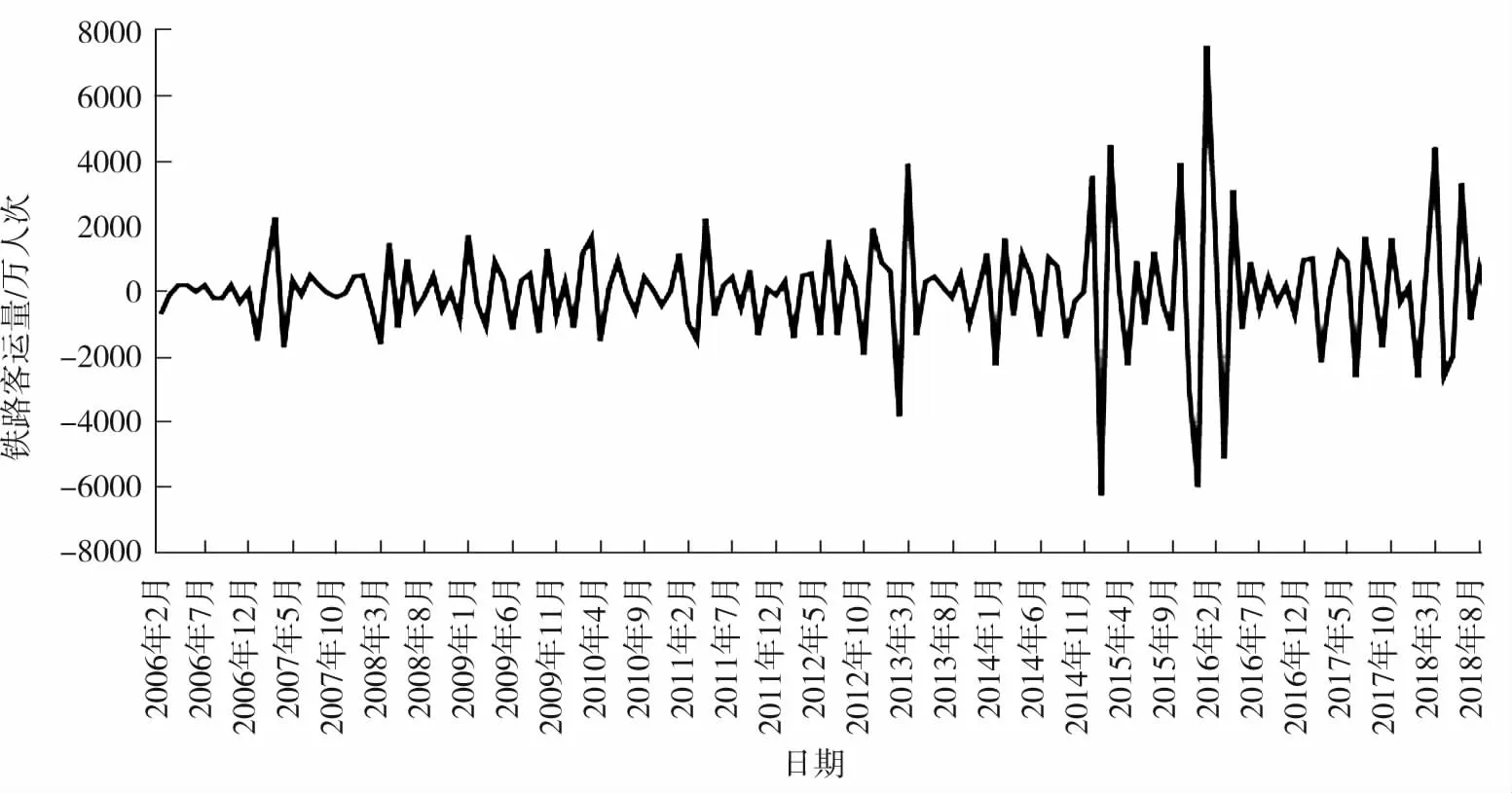
图2 差分处理后的时序图

差分后的自相关结果如表3所示，大部分自相关（autocorrelation）和偏自相关（partial Correlation）分别在（-0.200，0.200）（-0.130，0.130）内，Q-统计的相伴概率小于 0.05。

表3 差分后的自相关结果

为了更精确验证差分后的序列是否为平稳序列，对其进行ADF检验，结果如表4所示。检验统计量为-12.723 97，小于不同水平下的t-统计。因此，拒绝序列有一个单位根的原假设，检验结果为通过。

2.2.2 模型识别

对原序列进行一阶和季节差分后通过 ADF检验，确定SARIMA（p，d，q）（P，D，Q）s中，d=D=1，s=12。 仅依靠一阶差分和一阶季节差分中的自相关函数（autocorrelation function，ACF）及偏自相关函数（partial autocorrelation function，PACF）很难准确判定模型中p、q、P、Q的取值，本文根据赤池信息量准则（Akaike information criterion，AIC）、施瓦兹准则（Schwarz criterion，SC）并调整 R2识别模型的参数， AIC、SC越小，R2越大，可认为模型相对更优［23］。从高阶到低阶逐步测试p、q、P、Q的取值，根据最优准则确定模型为（2，1，1）（0，1，0）12。

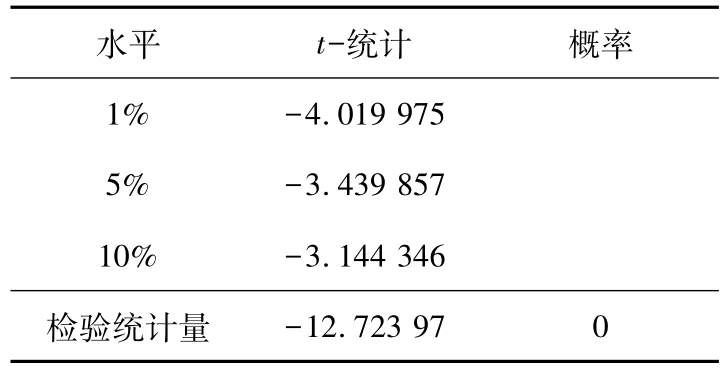
表4 差分后ADF检验结果

2.2.3 模型显著性检验和参数估计

生成的拟合残差序列如图3所示（残差曲线以左侧轴为纵轴，其余以右侧轴为纵轴）。

白噪声残差检验结果如表5所示。自相关和差分后的自相关结果分别置于（-0.200，0.200）（-0.150，0.150）内，Q-统计的 P＞0.05，说明选用的（2，1，1）（0，1，0）12模型对数据的拟合效果较好，预测结果通过检验。

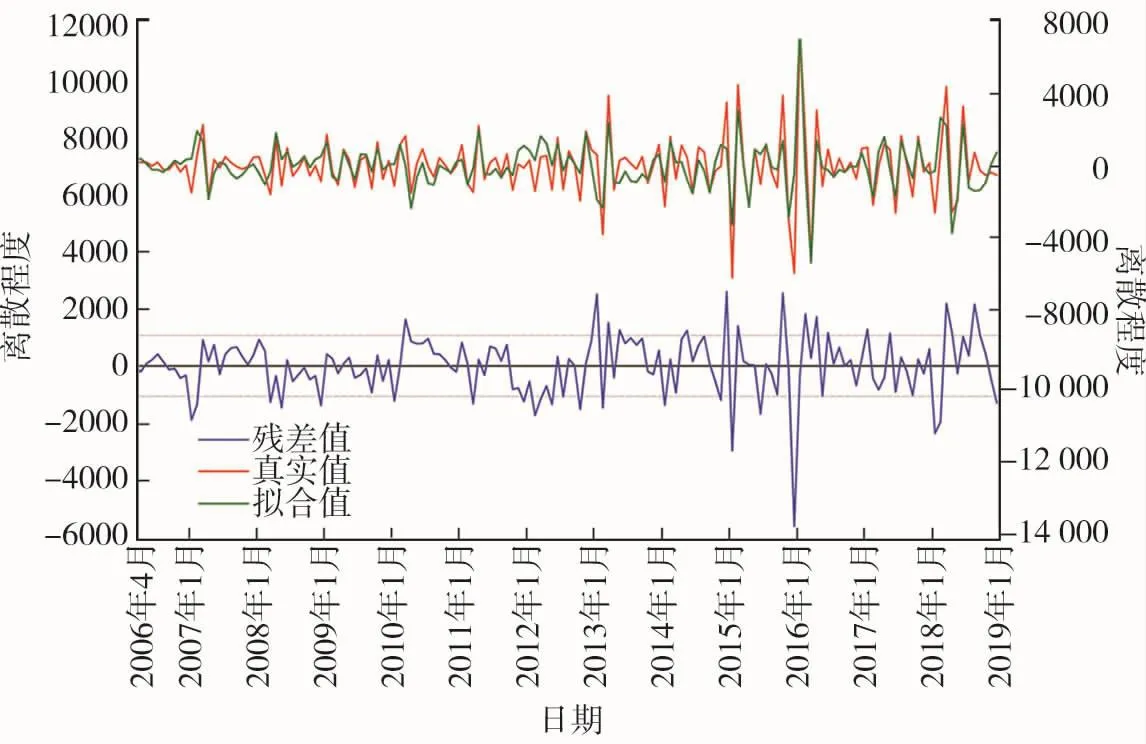
图3 拟合残差序列

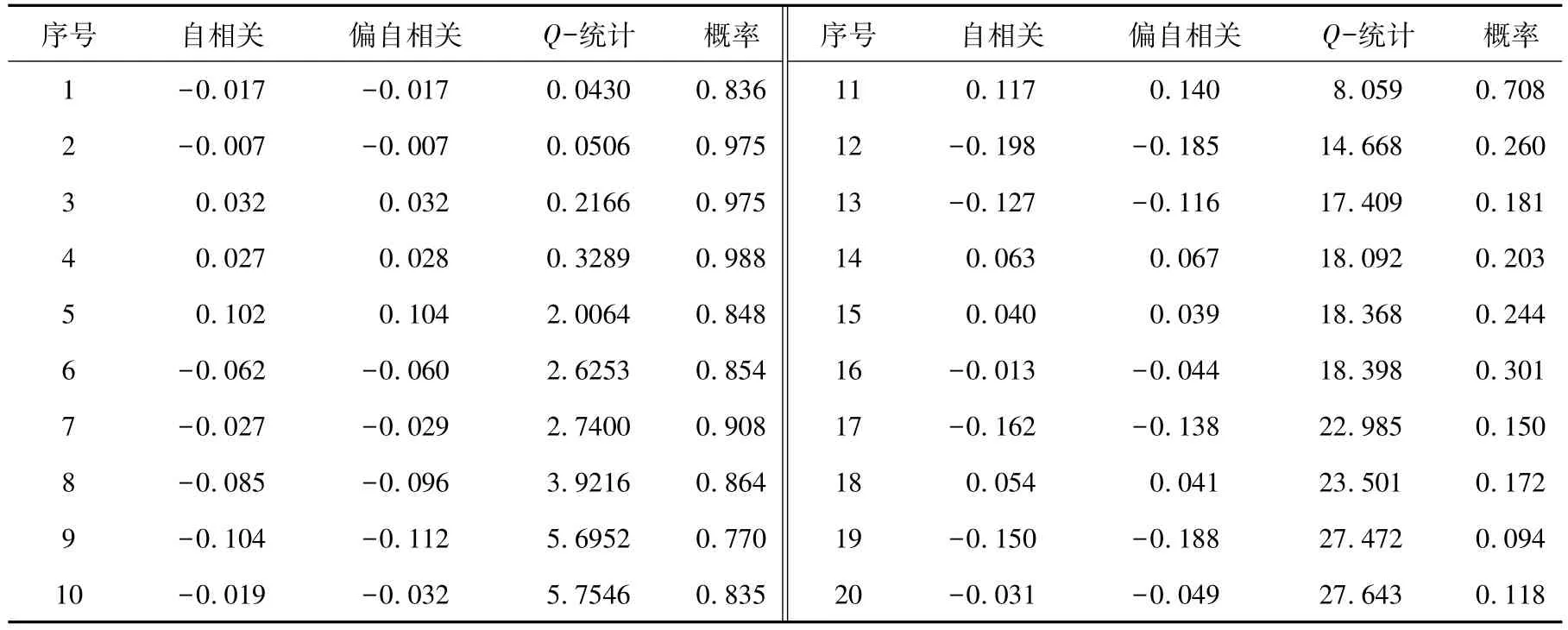
表5 白噪声残差检验结果

应用最小二乘法估计模型参数，如表6所示（c为常数）。

模型具体形式为：

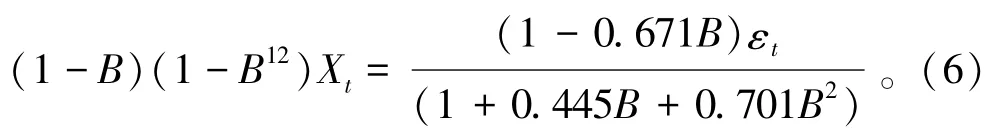
2.2.4 模型预测

SARIMA模型预测结果如表7所示，预测结果均在95%置信区间内，整体效果如图4所示。

表6 模型参数估计

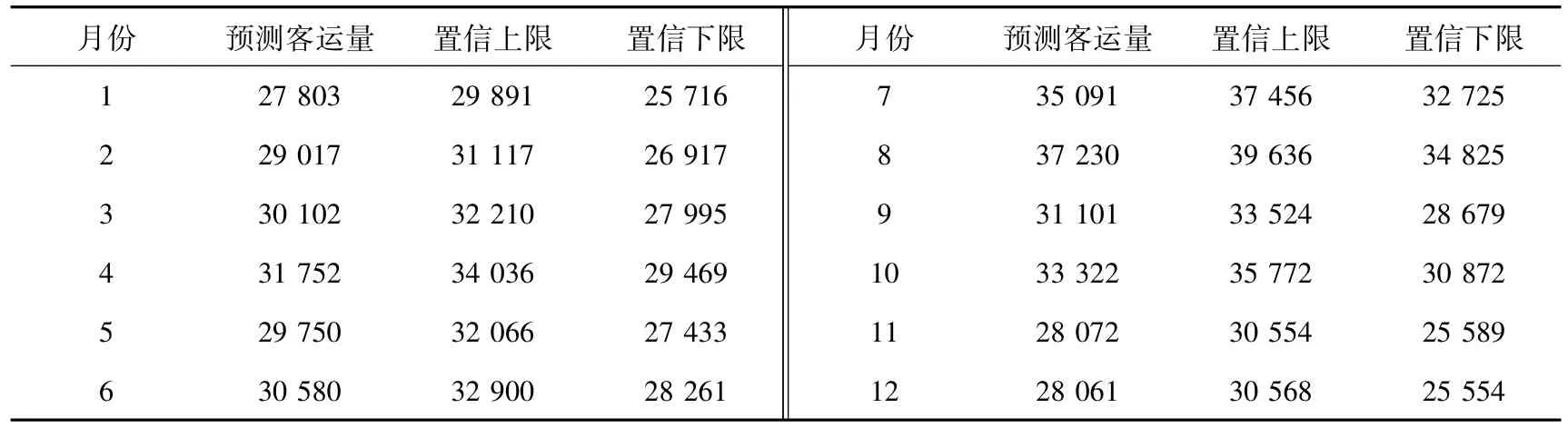
表7 2019年铁路客运量SARIMA模型预测结果 万人次

SARIMA（2，1，1）（0，1，0）12模型对铁路客运量的拟合值与实际值贴合度较高，说明对周期波动性提取较为充分。

图4 SARIMA模型预测曲线

3 预测结果分析

比较2种模型的预测精度，用均方根误差Re和平均绝对百分比误差Mape两种方法作为评价指标，评定预测客运量的准确性，公式分别为：

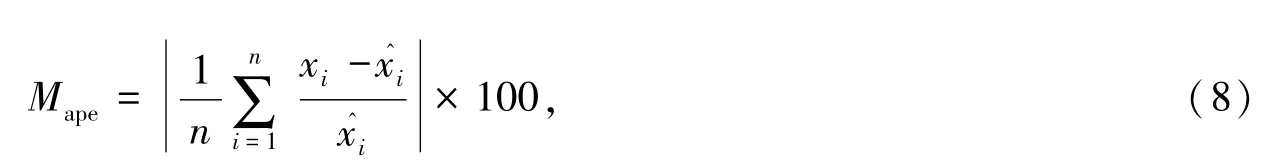
式中：xi为铁路客运量时间序列中第i个实际客运量，为铁路客运量时间序列中第i个预测客运量。

经计算，预测结果如表8所示。

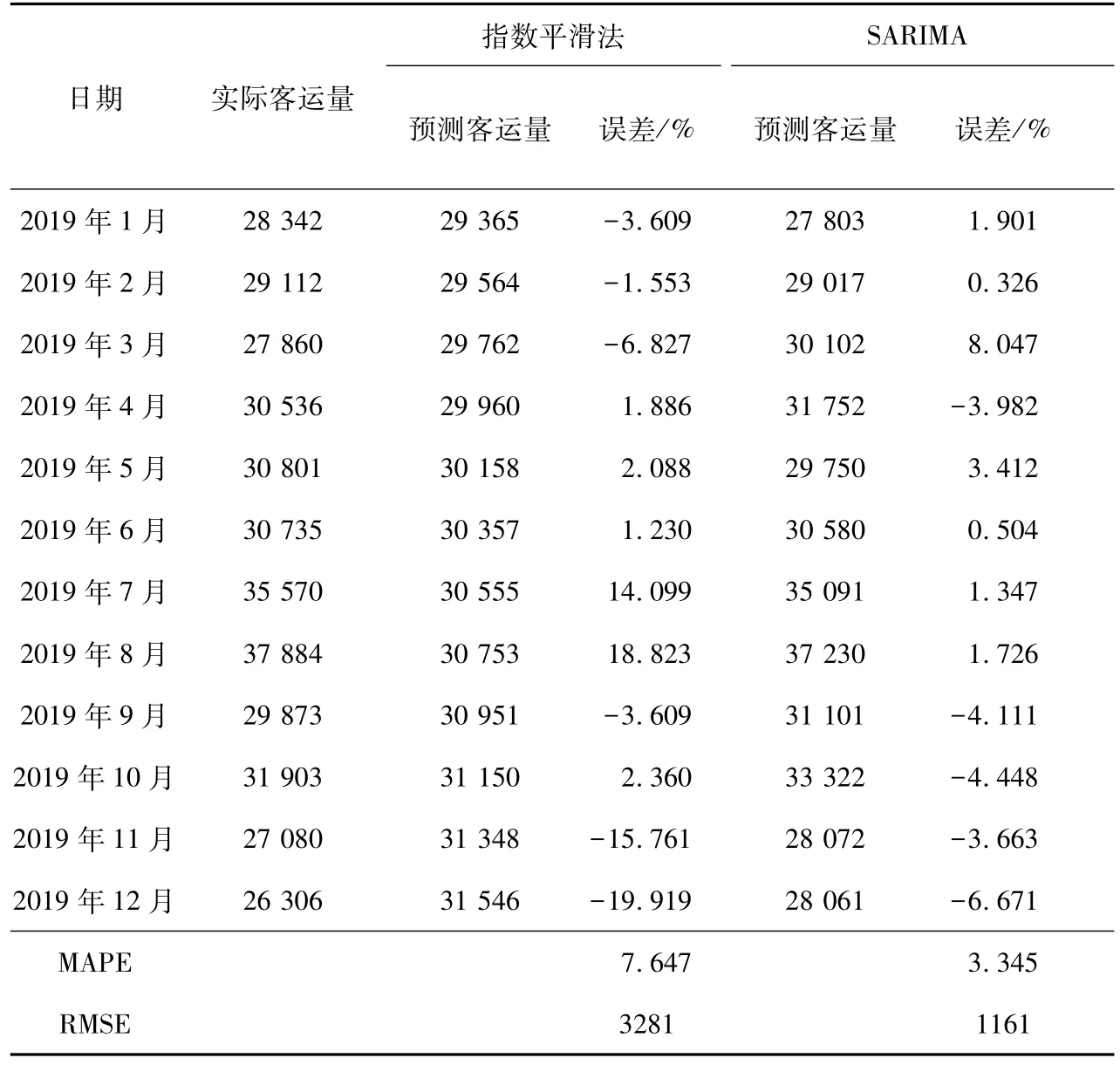
表8 我国铁路客运量预测及比较 万人次

结果表明：利用SARIMA模型的误差范围为-6.671～8.047，其中有10个月的铁路客运量误差在5%以内，MAPE为3.345%，预测能力为一级［18］。指数平滑法的预测误差范围为-19.919～18.823，最大误差约为20%，MAPE为7.647%，小于10.000%，虽然整体预测能力效果较好，但RMSE为3281，而SARIMA模型的RMSE为1161，说明指数平滑法的实际客运量与预测客运量间偏差较大。采用SARIMA模型预测客运量的精度远高于指数平滑法，前者的RMSE减少64.61%，MAPE减少56.26%。

因此，SARIMA模型可以更好地获取客流时间序列内部季节性及周期性规律，对时间序列中数据间的作用关系把控较好，可较好地预测短期内客流时间序列的发展趋势，预测结果表现较优。指数平滑法总体预测效果较差。

4 结语

铁路部门制定的相关规划大多是年度规划，相关学者的研究主要依据年度统计数据进行预测。但历史长期客流在时间序列上具有季节性、周期性的特点，分析现有数据，运用时间序列精度较高的Winters乘性指数平滑法和SARIMA模型，预测2019年各月的客运量。结果表明：采用指数平滑法预测铁路客运量，其MAPE为7.647%，RMSE为3281；采用SARIMA模型预测铁路客运量，其MAPE为3.345%，MAPE为1161。因此，SARIMA模型更适合预测铁路客运量，为铁路的行车组织方案及人员配备等提供重要依据。