抽水蓄能机组不稳定现象的流动机理与控制方法
罗先武 ,叶维祥 ,杨丹丹 ,冉红娟
(1.清华大学二氧化碳减排与资源化利用技术北京市重点实验室,北京市 100084;2.清华大学水沙科学与水利水电工程国家重点实验室,北京市 100084;3.上海交通大学机械与动力工程学院,上海市 200240)
0 引言
由图1所示的2018年中国能源构成可知,超过2/3的电量仍然来自燃煤发电[1],这给中国实现温室气体减排、减少大气污染等社会发展目标带来巨大压力。而近年来风力发电、光伏发电等可再生能源得到高速发展,在电力市场中所占据的比例逐年提升,又使得中国电力系统的稳定性面临严峻的挑战。为此,大力发展水电,尤其是大容量抽水蓄能,增强整个电力系统的快速调节能力是解决目前中国电力生产矛盾的重要策略。因而发展高水头抽水蓄能技术,不断提升在负荷快速转换期间的机组稳定性、保证抽水蓄能电站应对电力负荷快速转换能力是至关重要的。

图1 中国发电量比例Figure 1 Ratios of different power generation in China
图2列举了自20世纪60年代以来国内外抽水蓄能电站的设计水头分布[2],充分说明了现代抽水蓄能技术不断朝着高水头、大容量方向发展的趋势。中国近期建成或在建的大型抽水蓄能电站水头也大都超过了500m。高水头抽水蓄能技术不仅对电站机组结构提出了更高的要求,而且更加强调机组在偏离设计负荷工况下的运行质量。已有研究表明,当运行在偏离设计工况时,抽水蓄能机组内部往往出现非定常不稳定的流动现象,如作为水轮机运行的发电工况下存在旋转失速[3];而在偏低负荷泵工况时抽水蓄能机组易发生强烈的水压脉动,水压脉动可诱发间歇性空化[4],而不均匀的压力脉动引起转轮的径向力波动、转子动力学不稳定[5],严重时导致机组强烈振动[6]、叶片裂纹或转轮上冠断裂[7]。通常情况下,抽水蓄能机组在泵工况下的非稳定性问题较水轮机工况更严重,有时甚至威胁到机组与电站的安全性。所以,抽水蓄能机组泵工况的非稳定流动特性及其机理是水电设备行业长期的热点研究方向。

图2 抽水蓄能电站水头变化趋势[2]Figure 2 Pumping head variations for pumped storage power-stations[2]
抽水蓄能机组泵工况下的强烈水压脉动源自转轮与活动导叶之间的动静干涉。活动导叶进口靠近转轮下环侧发展的强漩涡引发相邻导叶流道内的逆流,使得导叶流道中的流动经历通畅—堵塞—逆流—堵塞—通畅的周期性循环过程[8];而在周期性循环过程中由于流道被堵塞导致导叶内水力损失急剧增大,进而体现为性能曲线或特性曲线的驼峰[7]。由于性能曲线或特性曲线的驼峰是水力旋转机械内部流动不稳定的外在表现,所以通过研究内部不稳定流动机理进而提出抑制驼峰的工程策略是未来进一步发展抽水蓄能技术的必然途径。尽管针对驼峰现象的研究历史可追溯至20世纪70年代,但仍需深入梳理已有研究数据以清晰揭示抽水蓄能机组泵工况下的不稳定流动特性,并基于机组内部流动的基本特性确定合理的工程措施来抑制驼峰现象、从而增强机组的运行稳定性。
1 抽水蓄能机组不稳定特性的预测
1.1 泵工况不稳定特性
图3表示通过模型试验测得的抽水蓄能机组某开度下泵工况的特性曲线[9]。横坐标表示无量纲化流量,数值为运行流量与最优效率点流量(QBEP)之比;纵坐标为无量纲化扬程,为运行扬程与最优效率点扬程的比值。结果表明特性曲线在0.70QBEP、0.90QBEP附近分别都出现驼峰,这两处驼峰在图中分别以PS1、PS2表示;两种记号“*”“o”分别对应试验中不同流量调节方向的工况点,记号的大小表征相应工况下测得的压力脉动幅值。由图3中的结果可知,沿着不同流量调节方向进行试验时驼峰出现的流量范围及对应的压力脉动都有所不同,这种现象称为“现象”。但在图3所示的结果中,两种不同流量调节方向对应的迟滞现象并不显著;无论是从小流量至大流量方向还是从大流量朝小流量方向变化,驼峰PS2工况(如B点)的压力脉动均比驼峰PS1工况的压力脉动更强烈。
对于图3所示的特性曲线驼峰,其中PS1对应的流量较大,可称为高部分负荷驼峰;而PS2对应的流量较小,按照习惯可称为部分负荷驼峰。所以,在泵工况下抽水蓄能机组中出现部分负荷驼峰时水压脉动更强,而流量调节方向并不改变这一性质。
对于驼峰PS1,特性曲线波峰对应的工况点约为0.91QBEP,特性曲线谷底对应的工况点约为0.87QBEP(以试验中特性曲线明显不稳定的流量下降方向为主要参照工况)。在模型试验中,在驼峰PS1附近所有工况下皆能捕捉到频率为0.2fn(fn:转轮旋转频率)的水压脉动分量。相比之下,特性曲线波峰处(即图中A1点)的压力脉动幅值较小,而特性曲线谷底处(图中A2点)的压力脉动强烈。
对于驼峰PS2,特性曲线波峰对应的工况点约为0.71QBEP(即图中B1点),特性曲线谷底对应的工况点约为0.68QBEP(图中B2点)。在模型试验中,特性曲线波峰工况时可以观察到转轮叶片进口的片状空泡,而特性曲线谷底工况时可以观察到转轮叶片进口附近的间歇性漩涡。由于机组内部的流动比较复杂,驼峰PS2附近的压力脉动频率不规则,可捕捉到0.14fn、0.8fn等多种复杂成分[10]。所以,在部分负荷驼峰工况下空化、漩涡与大规模流动分离团等非稳定现象及其耦合作用导致了机组内部激增的水力损失与强烈的压力脉动。

图3 抽水蓄能机组泵工况特性曲线的驼峰Figure 3 Positive slope at characteristic curve for pumped storage unit at pump mode
1.2 不稳定特性的数值预测方法
由于特性曲线驼峰属于水力机械内流不稳定的外在体现,主导该现象的内在流动机理则需要通过计算流体力学方法进行分析。因而,为适应工程应用的需求,在抽水蓄能机组设计阶段就准确模拟机组的内部流动,进而预测泵工况的不稳定特性具有十分重要的实际意义。
目前常用RANS(reynolds-averaged navier-stokes,雷诺平均纳维—斯托克斯)方法来预测抽水蓄能机组实际运行中的不稳定特性。实践证明,RANS方法虽然可能部分捕捉泵工况下的不稳定特性,但仍存在解析精度不足的问题。图4用空心圆记号表示基于k-ωSST湍流模型计算的扬程系数[11]。与实验数据(图中以实心方块记号表示)相比,采用RANS方法预测的扬程系数变化趋势与试验结果并不一致,尤其在驼峰处的预测误差较大,说明基于RANS方法预估的泵工况特性还不能满足实际工程的要求。为了提高计算精度,已有研究尝试将LES(large eddy simulation,大涡模拟)方法应用于抽水蓄能机组的不稳定特性预测。为了开展LES计算,将抽水蓄能模型机组(转轮外径为523.5mm)内部流动的雷诺数降低25倍、采用8.5×107个网格单元进行了大涡模拟。图5给出了LES、RANS两种方法预测的结果与模型试验的对比,表明大涡模拟可以比较准确地预测特性曲线驼峰位置的流量系数,以及机组内旋转失速团的传播速度,这些计算数据均接近模型试验得出的数据[12]。根据图5(b)可以推论,采用LES方法比URANS(unsteady RANS,非定常RANS)方法预测抽水蓄能机组泵工况非稳定特性具有明显的优势。
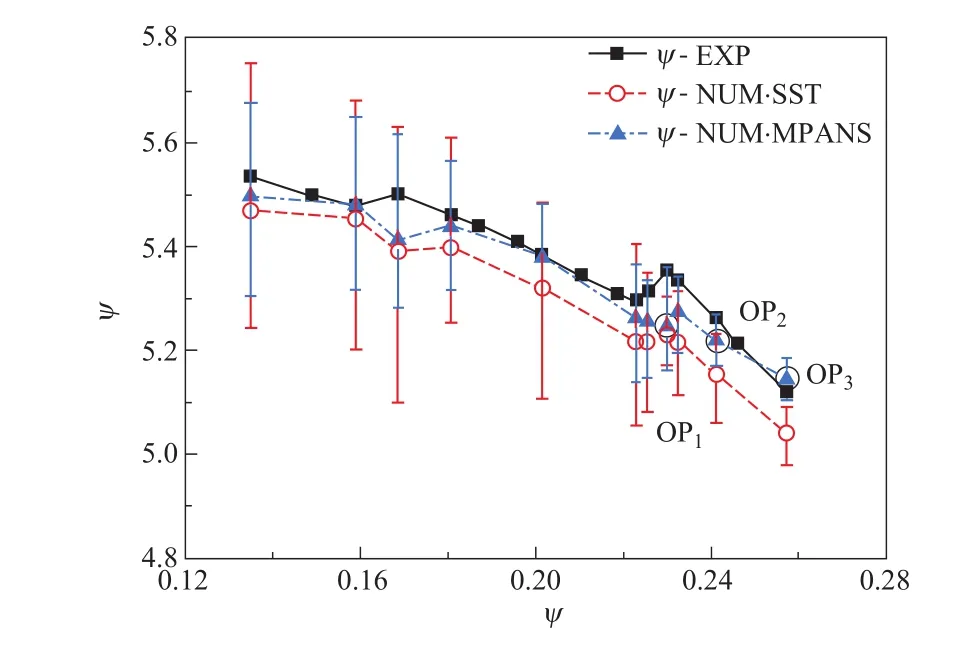
图4 抽水蓄能机组泵工况不稳定特性[11]Figure 4 Unstable characteristics for pumped storage unit at pump mode[11]
即使大涡模拟的预测精度较好,但由于计算成本过高,要开展抽水蓄能机组不稳定特性的LES分析还很困难。在图5中,仅对模型机组特性曲线的一个工况点(图中工况点Ⅲ)进行了大涡模拟,而且还须降低雷诺数以适应计算中的硬件资源。由此可见,在短期内大涡模拟尚不能全面用于抽水蓄能技术研究,尤其难以直接用于抽水蓄能原型与模型机组的不稳定特性分析。因此,为了促进中国抽水蓄能技术健康发展,有必要研究一种合理匹配预测精度与计算资源需求的不稳定流动特性数值模拟方法。
1.3 动态PANS模拟方法
在图4中,除了URANS模拟数据之外,还给出了基于PANS(partially averaged navier-stokes)方法预测的结果。图中“MPANS”表示一种改进的动态PANS方法[13]。PANS方法是一种介于DNS(direct numerical simulation,直接数值模拟)与RANS之间的桥接模型,根据模型系数的动态变化,可使PANS兼具DNS在复杂流动区域的精细模拟与RANS模拟主流的快捷模拟两种优势。
对于不可压缩非定常流动,动量守恒方程如下:

式中:p——压力;
ν——运动黏性;
Vi、Vj——沿i、j方向的速度,Vi由求解的速度分量Ui和未求解速度分量ui组成,即:

式中:< >为部分平均操作符。
部分平均的Navier-Stokes方程可表示为

式中:τij类似于RANS方法中的雷诺应力与LES中的亚格子应力,τij=
基于标准k-ε湍流模型的动态PANS模型为
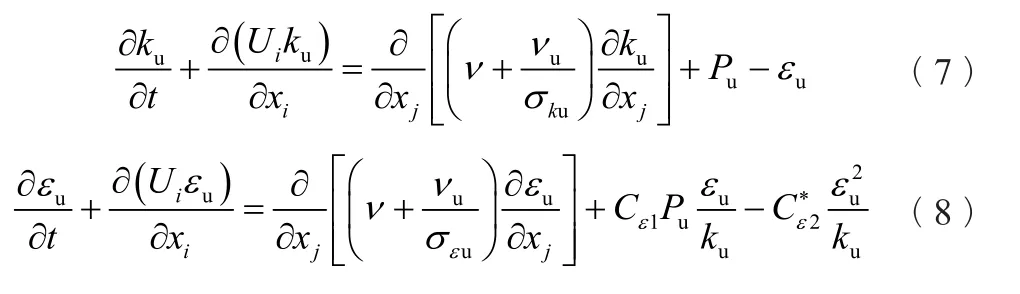
式中:u——未求解量;
k——湍动能;
ε——湍动能耗散率;
νu——;
P——湍动能生成项。
模型系数Cε1=1.44、Cε2=1.92、σk=1.0、σε=1.3,其他系数可由下式求出:
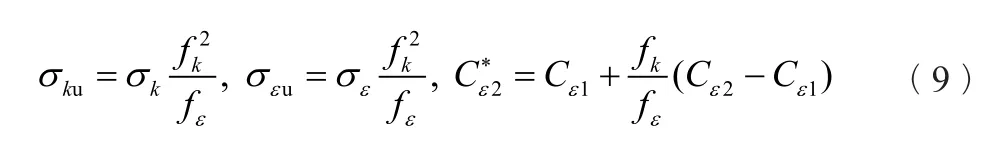
式(9)包含两个系数fk,fε。其中fk为未求解的湍动能ku与全部湍动能k之比,fε为未求解的湍动能耗散率εu与湍动能耗散率ε之比。这两个系数可按照公式(10)计算:

式中:l——混合湍流尺度,l=k1.5/ε;
Δ——局部网格尺度,l=(ΔxΔyΔz)1/3。
由式(10)可知,任意质点处的fk取决于流场中混合湍流长度与局部网格尺度。所以,动态PANS模型属于一种依据流场特性自动调整模型参数的湍流模拟方法。
图4的结果表明,与传统的RANS方法相比,采用动态PANS模型的数值计算过程相对稳定,扬程系数的变动范围比较小,由动态PANS预测的扬程变化趋势和试验测量结果基本一致,而驼峰OP1处的扬程更接近试验值。

图5 计算结果与试验数据的对比[12]Figure 5 Comparisons for numerical simulation and experimental data[12]
随着研究的不断深入,针对基于标准k-ε湍流模型的动态PANS模型,提出了不同修正策略的PANS方法。如文献[14]中构建了一种考虑流道曲率与旋转效应的新PANS方法,该方法用于模拟小流量工况下离心式叶轮内部非定常流动,更细致地揭示了性能曲线驼峰对应的叶轮内不稳定漩涡演化[15]。改进后的PANS方法可以更有针对性地解决实际流动的精细化模拟问题,从而为解决工程问题提供更有价值的指导。
2 机组内部流动不稳定机理
2.1 不稳定工况下的内部流场特征
图6表示泵工况的特性曲线及三种部分流量工况下叶轮内的平均流动[16],其中图6(b)为PIV试验结果,图6(c)为基于动态PANS模型的计算结果。在外特性方面,采用动态PANS模型能较好地预测泵工况的特性曲线,尤其是驼峰附近波峰与谷底之间的扬程变化趋势;在内流方面,采用动态PANS模型的数值模拟基本复现了PIV试验中捕捉的叶片间流道内大规模流动分离及漩涡。PIV试验与数值模拟的结果均显示了在部分流量工况下叶轮中平均流动的复杂性:在φ=0.5φbep与φ=0.6φbep两种工况下,在所有叶片间流道内都出现了较大尺度的流动分离,而这些分离团不仅出现在叶片吸力面,也出现在叶片压力面,它们对叶轮内的主流形成了一定的阻塞效果。如φ=0.5φbep时,在叶片间流道A、B、C中的阻塞效果特别显著,而在叶片间流道D、E内的阻塞效果相对较轻;在φ=0.78φbep时,流动分离团的尺度相对较小,且主要出现在叶片吸力面靠近叶轮外径处。此时流动分离对主流的影响相对较小。
图7表示抽水蓄能模型机组泵工况下不同时刻活动导叶内的流速分布[12]。图7(f)给出了14个转轮旋转周期内,流经两个活动导叶之间的流量变化曲线,流量测量断面位于活动导叶GVA与GVB之间,即图7(a)中的红色断面。图7(b)中,活动导叶GVA与GVB之间的流动畅通,此时对应最大的流量;而图7(d)中,源自GVB吸力面的流动分离逐渐扩大,并基本占据了活动导叶GVA与GVB之间的流道,使得流速矢量都转向切线方向,此时由于流道的堵塞,通过GVA与GVB之间的流量急剧下降,接近了最小流量。流道的严重堵塞将直接导致水力损失的激增,是抽水蓄能机组泵工况下出现特性曲线驼峰的根源。
由图7(f)可知,驼峰工况下活动导叶中的不稳定流动引起流动分离并逐渐阻塞流道;通过导叶间流道的流量呈周期性变化。这种周期性变化的流动诱发强烈的水压脉动。图8表示在转轮出口至活动导叶之间的无叶区所监测的水压脉动。在图8(a)中,实线为瞬时压力脉动,而虚线表示是以转轮旋转频率fn为限的低通滤波曲线。由图8(b)所示的结果可知,除了转轮叶片(转轮有9个叶片)通过频率9fn的脉动成分,及其2倍谐频(18fn)成分之外,压力脉动还包括一个明显的低频成分,其频率仅为转轮旋转频率fn的7.6%。总体上,图8中的三种压力脉动成分都属于旋转的转轮与静止部件之间动静干涉的结果,但它们的原理却不同:转轮叶片通过频率及其2倍谐频的两种压力脉动分量都是抽水蓄能机组结构引起的,即转轮的旋转叶片与导叶、蜗壳等静止流道直接干涉的结果;而7.6%fn的低频压力脉动分量虽然也源自结构干涉,但该压力脉动则反映了由于结构干涉诱发不稳定流动的影响,可以看成是一种间接的干涉效果。

图6 部分负荷工况下叶轮中的平均流动[16]Figure 6 Averaged flows in pump impeller at part load operations[16]
2.2 不稳定流动结构的传播
在图7(f)中,流经导叶GVA与GVB之间的流量随时间呈现周期性变化。由于流量变化,必定引起导叶进口处的流速大小与方向发生变化,这样在活动导叶进口发生了液流冲角的急剧变化。在图4的结果基础上,图9中显示了无叶区不同位置处水流冲角AOA的变化;其中横坐标采用了以角度表示的无叶区相对位置,纵坐标为水流冲角AOA。三种工况OP1、OP2、OP3分别对应抽水蓄能模型机组泵工况下的驼峰点、高部分负荷点及最优效率点,如图4所示。当机组运行在最优效率点OP3时,水流冲角AOA尽管随时间波动,但变化幅值较小;而当机组运行在驼峰工况OP1时,水流冲角不仅随着时间变化,而且在同一时刻沿周向不同位置处的水流冲角也出现了剧烈变动,其中在约80°、200°和320°的周向位置出现了冲角峰值,这些峰值对应着发生不稳定流动的典型区域。为了清晰展现转轮至导叶之间的不稳定流动,图10(a)中显示了两条参考线,其中“line 1”靠近活动导叶进口,而“line 2”则靠近转轮外径。图10(b)的结果表明,在驼峰工况点(OP1)转轮外径处的水流角α沿“line 2”分布很不均匀,在叶片出口附近水流角甚至接近零,而在θ=112°处的水流角则将近20°。这种不均匀出流对活动导叶进口附近的流动产生了重要影响,使得AOA沿“line 1”的分布出现大幅度变化,如在θ=85°处水流冲角达17.5°,而在θ=115°处冲角为-2.5°。由图10(a)中的速度矢量可知,此时不同导叶之间流道内的流动状态具有显著差异,如导叶A与导叶B之间流道内出现了回流,导叶B与导叶C之间的进口基本被封闭、流道被堵塞,而导叶C与导叶D之间流道则完全通畅,流速很大。
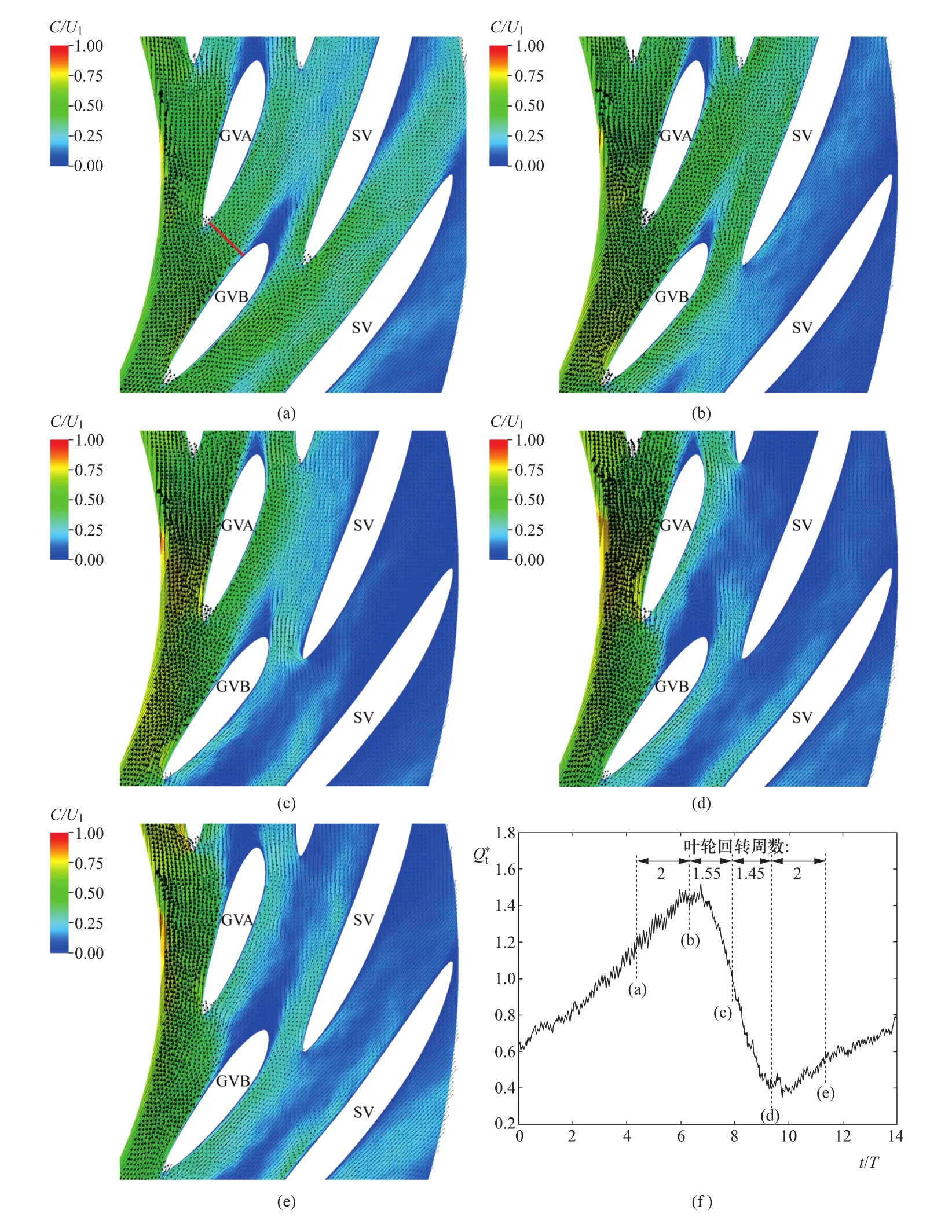
图7 驼峰工况下活动导叶内的流速分布[12]Figure 7 Instantaneous flows in guide vanes at positive slope condition[12]
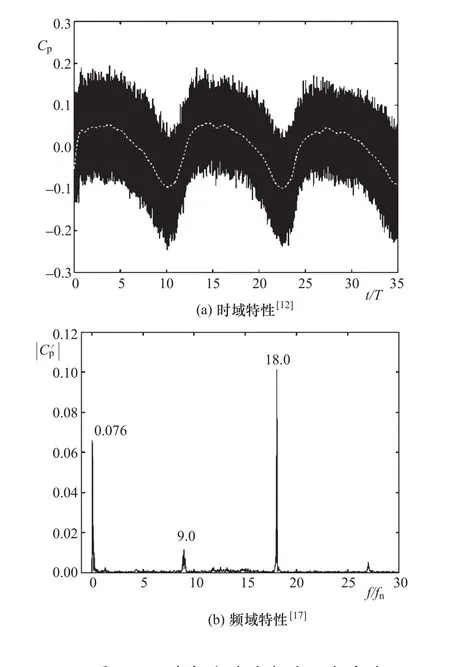
图8 不稳定流动诱发的压力脉动Figure 8 Pressure oscillations induced by unstable flow

图9 三种工况下活动导叶进口的冲角变化[11]Figure 9 Attack of angle at leading edge of guide vane at three operations[11]
事实上,即使在驼峰工况,这种导叶间流道内的“回流—堵塞—通畅”周期性流动特征并非在抽水蓄能机组静止部件的全域中出现。在刻画了驼峰工况(OP1)机组内不稳定流动的图11(a)中,出现了3组不稳定流动结构(虚线框内),而且同时发生在活动导叶与固定导叶中。这种不稳定流动结构涉及流道的堵塞,通常可称为“失速团”(stall cell)。由图9可知,三组失速团之间的相位差约为120°;在部分负荷工况(OP2),机组内流动得到很大改善,尽管在导叶附近的局部位置出现了轻微流动分离,但流道内的流动比较稳定;在最优效率点OP3,机组静止部件中的速度均匀性好,流动稳定,仅在靠近蜗壳隔舌的固定导叶中有极轻微的流动分离[11]。
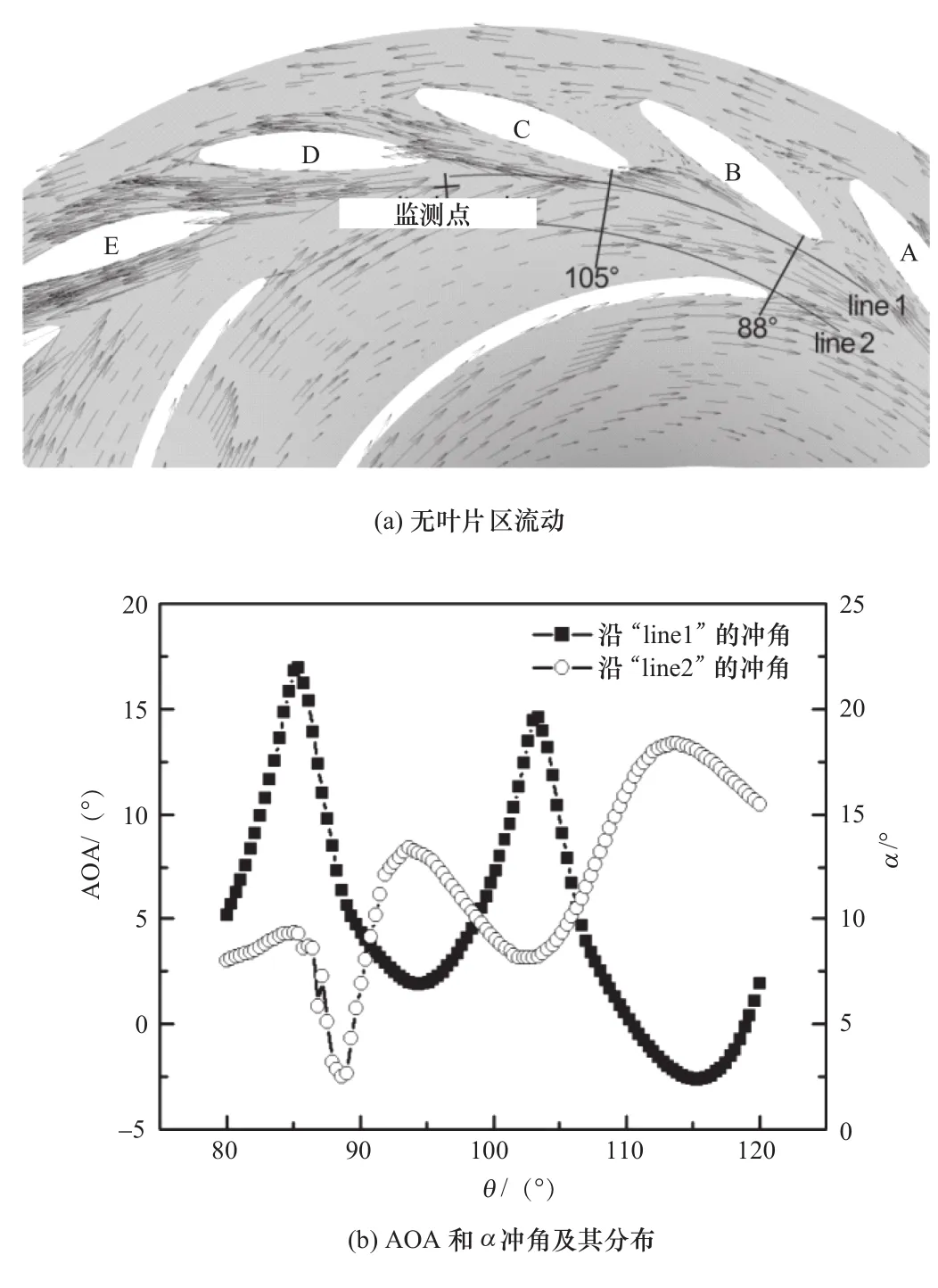
图10 OP1工况下无叶区流动的变化[11]Figure 10 Flow angle distribution at vaneless area at OP1 condition[11]
如图12所示,由逆流—堵塞—射流(指相邻导叶间流道中通过的流量超过导叶间流道的平均流量)组成了抽水蓄能机组泵工况的不稳定流动结构,即失速团。由于失速团一般随时间在机组内部流场中传播,所以也被称为旋转失速团(rotating stall cell)。通常情况下,失速团的传播频率低于转轮旋转频率fn。大量研究表明在流道中失速团的数量、传播速率均与运行工况密切相关,可以通过监测无叶区压力或者流场可视化试验确定[18]。在离最优效率点Qbep较近的高部分负荷工况下,流道中的失速团数量较少,一般为1~3个;随着流量继续下降,失速团数量增多,如图5所示。

图11 三种工况下机组静止部件内的流动[11]Figure 11 Flow in unit stationary components at three operations[11]

图12 导叶内不稳定流动的传播机制[11]Figure 12 Unstable flow propagation in guide vanes[11]
图13给出了泵工况下不同运行流量所对应的失速团传播速率比值[17]。图13中,Ω为转轮旋转速率;Ωrs为失速团的传播速率,可通过测量导叶进口处压力脉动波形并进行快速傅里叶变换得出。图13所示的试验结果中,当流量系数φ在0.042~0.087范围内变化时,流道内仅存在1个失速团。当φ=0.087时,压力脉动显著,噪声达75.5dB(A),失速团沿叶轮旋转方向传播速率为0.083fn;而流量系数φ小于0.042时,流道内存在2个失速团。当φ=0.042时,试验中测得的噪声降低至72.8dB(A),失速团沿叶轮旋转方向传播速率为0.0665fn。当流道中只有单个失速团时,失速团的传播速率可以直接通过流道中监测的压力脉动频率来确定;而当流道中存在n个失速团时,所对应的压力脉动频率是失速团传播频率的n倍。

图13 流道内失速团的传播速率[19]Figure 13 Propagation speed of rotating stall in pump impeller[19]
失速团传播速率Ωrs可由下列计算式[20]求出:

式中:Ω——转轮旋转角速度;
α0——导叶开度;
β2——转轮外径处的叶片安放角;
Ms——活动导叶与固定导叶中的流体质量;
Mr——转轮内的流体质量。
使用式(11)可以预估失速团在流道中的传播速率,可以为结构设计中避免机组共振提供一定的技术参考。
2.3 特性曲线驼峰的形成机制
抽水蓄能机组泵工况下,偏负荷运行条件易导致在叶轮出口的非均衡出流,进而由于动静干涉作用在导叶内诱发不稳定流动。在流量较小时,不稳定特性主要受大尺度分离流动、进口预旋等因素影响;而随着流量增大,流动分离的区域发生迁移,形成在导叶流道中传播的失速团。失速团的传播引起相邻流道的堵塞、逆流与射流,诱发显著的水力损失与水压脉动。
采用局部熵产率(local entropy production rate,LEPR)可以表征内部流动引起的能量损失。图14给出了开度为19mm、流量为0.74Qbep工况下转轮叶片四个不同展向流道内的局部熵产率与流线分布[21]。图中,“Dec”“Inc”分别表示逐步减小与逐步增大的流量变化方向。图中的结果表明,转轮内一旦发生了流动分离,尤其在叶缘附近有强烈的分离,就会出现很大的局部熵产率;对于不同的流量变化方向,叶轮中的流动有相似性,但同时也存在一定差异。图15给出了开度为19mm、不同流量工况下,尾水管(图中以“DT”表示)、叶轮(RN)、导叶(GVSV)和蜗壳(SP)中由熵产率转化的流动损失[22]。由此可知,偏低负荷工况下的机组损失中,导叶与叶轮的损失较大。而当运行流量小于0.8Qbep时,导叶中的损失将大于叶轮内的损失。如图14对应工况的流量为0.74Qbep,此时导叶中的损失接近4m,大于其他流动部件中的损失。
图15的结果也表明,无论哪种工况,转轮与导叶中的损失均较大。当机组运行流量大于0.9Qbep时,各种流动部件中的损失变化很小;而当运行流量小于0.8Qbep时,导叶、叶轮和尾水管中的损失同时急剧增大,使得机组水力损失遽然增大,导致泵工况的扬程陡降,这样在扬程—流量曲线出现扬程谷底现象,即性能曲线上的驼峰。

图14 不同展向转轮流道的局部熵产率与流线分布[21]Figure 14 Local entropy production rate and streamline distribution at different spanwise flow passages[21]

图15 主要流动部件的损失[21]Figure 15 Head loss due to entropy production and flow discharge at different flow passages[21]
3 机组不稳定特性的控制方法
不稳定流动可导致强烈的水压脉动,成为抽水蓄能机组安全运行的严重隐患。为了缓解抽水蓄能机组泵工况下的不稳定流动,在工程上可以从很多方面进行优化与控制[2],包括优化转轮设计,调整导叶开度、转轮与导叶的间距、转轮叶片安放角与包角,采用非同步导叶、长短叶片活动导叶、长短叶片转轮,以及在流场特定位置引入射流等。
3.1 转轮优化
转轮是抽水蓄能机组的能量转换单元,决定了泵工况下活动导叶之前的流动状态,所以转轮设计对特性曲线有重要影响。实践证明,设计非规则的叶片出口角分布规律[10]、采用长短叶片[23],以及改变低压边形状[24]等措施都可能改善或消除特性曲线驼峰,并适当提高机组的效率。从动静干涉的角度分析,优化转轮的设计对于抑制机组内部不稳定流动的重要性是不言而喻的。
图16是针对某抽水蓄能电站可逆式机组的两种转轮设计方案所对应的轴面流道轮廓图[25]。在第一种设计方案(图中Optimized A)的基础上,通过改变上冠(Hub)与叶片低压边(LP)曲线,扩大了转轮轴面流道所围成的面积以及低压边的流道截面,并基于反问题设计、试验设计法(DOE)、响应面法(RSM)、遗传算法等构建的优化设计方法进行叶片形状优化,设计新的转轮模型为图中Optimized B。图17比较了两种设计方案的模型转轮。从转轮低压边观察,Optimized A转轮的叶片朝正方向倾斜,而Optimized B转轮的叶片则朝负方向倾斜。
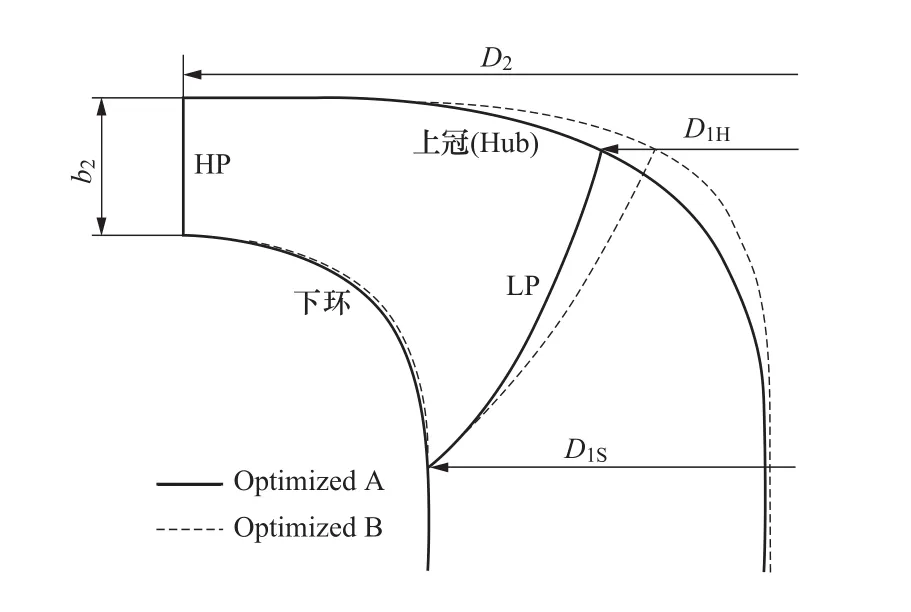
图16 可逆式转轮两种设计方案的轴面流道轮廓[25]Figure 16 Meridional sections of two design schemes for pumped storage unit runner[25]

图17 两种不同设计方案的可逆式转轮模型[25]Figure 17 Model runners of two design schemes for pumped storage unit runner[25]
图18为两种设计方案转轮模型的试验结果。在泵工况下,优化后的Optimized B转轮的模型机组性能得到明显改善:①基本消除了流量—扬程曲线的驼峰,避免了低负荷时的不稳定现象;②明显提高了低负荷工况的机组效率,且模型机组的最高效率略有增大,接近92%。

图18 两种可逆式转轮的机组性能曲线[25]Figure 18 Hydraulic performance comparison for two pumped storage unit runner[25]
3.2 非同步导叶或异形导叶
由图15可知,导叶中的损失较大,尤其在偏低负荷工况下损失可能剧增,从而导致性能曲线驼峰。因此,导叶的设计以及导叶在机组中的布置方式都能影响抽水蓄能机组的内部流动,进而造成机组的不稳定性能。
为保证抽水蓄能机组的稳定运行,目前工程中常用预开导叶的方法,即在小开度下预先开启若干导叶至指定开度来缓解机组内部流动的不稳定性[26],而预开导叶方案需要通过研究进行优化配置。图19表示抽水蓄能机组中水力部件布置的示意图。当四个导叶(图中gv3、gv4、gv13、gv14)的开度保持一致,且大于其他活动导叶的开度时,机组内部压力脉动发生变化。在静止部件中的压力脉动得到较明显抑制,但转轮中的压力脉动有所增强[27]。需要指出,采用非同步导叶开启方式在一些工况下可以改善机组内部流动与动静干涉引起的压力脉动,但不利于设计工况下形成轴对称流动条件。因而,无论是采用非同步开启导叶,还是设计非对称分布的导叶,都需要统筹考虑在全运行区域下的机组性能。
研究还表明导叶高度对抽水蓄能机组内不稳定流动造成的动静干涉及转轮应力有一定影响。如针对某500m水头级抽水蓄能机组,将导叶高度增大约40%,可使水轮机工况下的主应力降低20%~30%[28],改善了机组的运行安全性。
近年来,基于仿生学原理设计的导叶在抽水蓄能机组中得到应用[29],如采用不同波浪形导叶头缘来抑制特性曲线驼峰。在选择合理的凸起高度(2A)、展向波长(λ)时,可以在维持机组运行效率不变的前提下缓解内流的不稳定,降低在偏低负荷工况下的流动损失(见图20)。

图19 可逆式机组非同步导叶分布方案[27]Figure 19 Distribution scheme of misaligned guide vanes for pumped storage unit[27]

图20 曲线形头部的导叶[29]Figure 20 Guide vane with leading-edge protuberance[29]
3.3 导叶关闭/开启规律
大量的工程经验说明,合理的导叶关闭/开启规律是保证抽水蓄能机组安全与电站稳定运行的必要条件。一般建议采用导叶开度分阶段开启方式,使得在导叶开启过程中每个阶段的水压和轴功率波动幅度均较小且能够很快衰减,确保机组稳定运行,并尽量减小电机功率突变对电网的冲击[30]。
为了获得最优的导叶关闭/开启规律,需要对每个关闭/开启阶段的参数进一步优化。图21对比了两种不同的调节方案。基于NSGA-II遗传算法的多目标优化方法确定两段式导叶关闭曲线,并合理调整调压井与水库之间的距离,可使抽水蓄能电站最大超压量减小4.2%,最大超速减小 7.1%[31]。
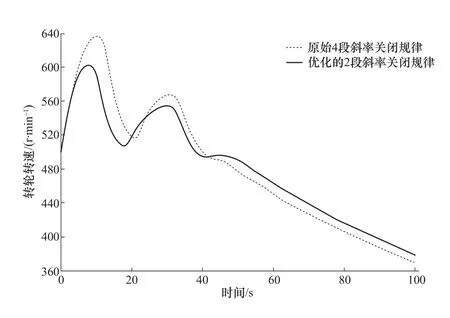
图21 两种不同导叶关闭曲线[31]Figure 21 Two curves for guide vanes closing[31]
4 结语
截至2018年底,中国抽水蓄能电站在运装机容量达3002.5万kW,在建抽水蓄能电站装机容量约4321万kW,在运、在建装机容量均已稳居世界第一位[32]。随着中国能源战略实施与能源结构进一步优化,抽水蓄能在电力系统中将发挥巨大作用,未来还会得到迅速发展。因而,不断研发先进的抽水蓄能技术、稳步推进中国抽水蓄能电站建设势在必行。
抽水蓄能机组泵工况不稳定特性具有极其复杂的物理机制。经过多年研究,人们已部分理解驼峰工况下机组内部不流动特性,以及造成损失剧增的机理,进而采取相应的工程措施来改善机组的稳定性。尽管如此,目前对抽水蓄能机组不稳定流动机理并未达到全面、清晰而系统的认识,而无论是数值模拟还是试验手段都存在精度不足的问题,亟待通过大量深入的工作以不断改进研究方法,为解决抽水蓄能机组不稳定的工程实践提供技术支撑。
——“AABC”和“无X无X”式词语

